Korrelatsioon
Statistikas ja tõenäosusteoorias tähendab korrelatsioon seda, kui tihedalt on kaks andmekogumit omavahel seotud.
Korrelatsioon ei tähenda alati, et üks põhjustab teist. On väga võimalik, et tegemist on kolmanda teguriga.
Korrelatsioonil on tavaliselt üks kahest suunast. Need on positiivne või negatiivne. Kui see on positiivne, siis lähevad kaks kogumit koos ülespoole. Kui see on negatiivne, siis üks neist tõuseb ja teine langeb.
Erinevates olukordades kasutatakse palju erinevaid korrelatsioonimõõtmisi. Näiteks tõmbavad inimesed hajuvusgraafikule parima sobivuse joone, et näidata korrelatsiooni suunda.
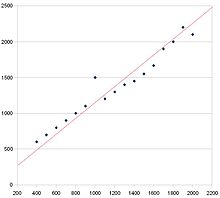
See hajuvusgraafik on positiivse korrelatsiooniga. Seda on näha, sest trend on ülespoole ja paremale suunatud. Punane joon on parima sobivuse joon.
Korrelatsiooni selgitamine
Tugev ja nõrk on sõnad, mida kasutatakse korrelatsiooni kirjeldamiseks. Kui on tugev korrelatsioon, siis on punktid kõik lähestikku. Kui korrelatsioon on nõrk, siis on kõik punktid üksteisest lahutatud. On viise, kuidas arvud näitavad, kui tugev on korrelatsioon. Neid mõõtmisi nimetatakse korrelatsioonikoefitsientideks. Kõige tuntum on Pearsoni korrelatsioonikoefitsient. Sa sisestad andmed valemisse ja see annab sulle numbri. Kui see number on 1 või -1, siis on tegemist tugeva korrelatsiooniga. Kui vastus on 0, siis puudub korrelatsioon. Teine korrelatsioonikoefitsient on Spearmani korrelatsioonikoefitsient.
Korrelatsioon vs põhjuslikkus
Korrelatsioon ei tähenda alati, et üks asi põhjustab teist asja (põhjuslikkus), sest miski muu võib olla mõlema põhjuseks. Näiteks kuumadel päevadel ostavad inimesed jäätist ja inimesed lähevad ka randa, kus mõned saavad haisid süüa. Jäätise müügi ja haide rünnakute vahel on seos (mõlemad tõusevad, kui temperatuur tõuseb). Kuid see, et jäätise müük tõuseb, ei tähenda, et jäätise müük põhjustab (põhjuslikkus) rohkem hairünnakuid või vastupidi.
Kuna korrelatsioon ei tähenda põhjuslikkust, siis teadlased, majandusteadlased jne katsetavad oma teooriaid, luues isoleeritud keskkondi, kus muudetakse ainult ühte tegurit (kui see on võimalik). Poliitikud, müügimehed, uudisteagentuurid ja teised väidavad aga sageli, et teatav korrelatsioon tähendab põhjuslikku seost. See võib olla tingitud teadmatusest või soovist veenda. Nii võib uudislugu äratada tähelepanu, öeldes, et inimestel, kes tarbivad sagedamini teatavat toodet, on konkreetne terviseprobleem, mis viitab põhjuslikule seosele, mis tegelikult võib olla tingitud millestki muust.
Seotud leheküljed
- Cohen, J., Cohen P., West, S.G., & Aiken, L.S. (2003). Rakendatud mitmekordne regressioon/korrelatsioonianalüüs käitumisteaduste jaoks. (3. trükk) Hillsdale, NJ: Lawrence Erlbaum Associates.
Küsimused ja vastused
K: Mis on korrelatsioon?
V: Korrelatsioon on viis näidata, kui tihedalt on kaks andmekogumit seotud.
K: Kas korrelatsioon tähendab, et üks andmekogum põhjustab teist?
V: Ei, korrelatsioon ei tähenda alati, et üks andmekogum põhjustab teist. Tegelikult on sageli kaasatud ka kolmas tegur.
K: Millised on korrelatsiooni kaks suunda?
V: Korrelatsiooni kaks suunda on positiivne ja negatiivne.
K: Mida tähendab positiivne korrelatsioon?
V: Positiivne korrelatsioon tähendab, et kaks andmekogumit tõusevad koos.
K: Mida tähendab negatiivne korrelatsioon?
V: Negatiivne korrelatsioon tähendab, et üks andmekogum tõuseb ja teine langeb.
K: Kas on olemas erinevaid korrelatsiooni mõõtmisi?
V: Jah, erinevate olukordade puhul kasutatakse palju erinevaid korrelatsiooni mõõtmisi.
K: Kuidas näidatakse sageli korrelatsiooni suunda hajuvusgraafikul?
V: Inimesed joonistavad sageli parima sobivuse joone, et näidata korrelatsiooni suunda hajuvusgraafikul.
