Normaaljõud ehk normaalreaktsioon — määratlus, valemid ja näited
Tutvu normaaljõu määratluse, valemite (mg, mg·cosθ) ja praktiliste näidetega selgelt ja kokkuvõtlikult — ideaalne korduseks ja eksamiks.
Normaaljõud on kontaktjõud, millega maapind (või mis tahes pind) surub objekti vastu tagasi — täpsemalt, pind avaldab objektile jõudu, mis on alati pinnaga risti (täisnurga all). Normaaljõud on Newtoni III seaduse paariks pinnale mõjuvale kontaktjõule: objekt avaldab samasuguse suurusega, kuid vastassuunalise jõu pinnale. Kui normaaljõudu ei oleks, siis näiteks inimene "imbuks" aeglaselt pinnale sisse.
Suhtlus raskusjõuga ja valemid
Tavalistes olukordades, kus lisajõude (nt tõmbejõud, kiirendus, kõrgemõju) ei esine, võrdub normaaljõud objekti kehakaaluga. Tasasel horisontaalsel pinnal on normaaljõud
m g {\displaystyle mg} 
,
s.t. N = m·g (ühikud: N, newtonid).
Kaldu tasandit arvestades on raskusjõu komponent, mis surub objekti pinna vastu, võrdne mg cosθ, seega normaaljõud väheneb nurga võrra:
m g c o s θ {\displaystyle mgcos\theta}. 
Pange tähele, et tasasel pinnal oleks θ {\displaystyle \theta }
= 0, mistõttu c o s θ {\displaystyle cos\theta }
= 1 ja mõlemad avaldised langevad kokku.
Üldised juhtumid ja korrigeerivad avaldised
- Kui süsteemil on lisakiirendus suunaga, mis omab komponendi normaalsuunas (nt lift, mis kiirendab üles või alla), siis normaaljõud muutub: N = m(g ± a) (suund + kui kiirendus on suunatud pinnale vastu, − kui vastassuunaline).
- Kui pinnal on lisajõud (nt rakendatud jõud kallakul), tuleb nende vertikaalsed (normaalsuunalised) komponendid liita või lahutada, et leida resultant, mis määrab N. Üldine reegel: N on kõikide pinnaga ristuval suunal olevate jõudude summa, mille pinnale avaldatakse.
- Kaarduva pinna (nt kaarel liikumise) puhul võib inertsimassi tsentripetaalkiirendus muuta normaaljõu suurust: näiteks ringtrajektoori ülemisel punktis N = m(g − v²/r), alumisel punktis N = m(g + v²/r).
- Normaaljõud ei saa tõmmata pinda vastu; see on vaid suruv jõud. Kui normaaljõud muutub nulliks, kaotab keha kontaktpinna (nt hüpe või rajalt lahkumine).
Seos hõõrdumisega
Hõõrdejõud sõltub normaaljõust: liikumist takistav kinetiline hõõrdumine on tavaliselt F_k = μ_k N ja staatiline maksimaalne hõõrdumine F_s,max = μ_s N, kus μ_k ja μ_s on vastavalt kineetilise ja staatilise hõõrdumise kordajad. Seega normaaljõu muutus mõjutab otseselt hõõrdejõu suurust.
Lihtsad näited
- Blokk massiga 5 kg tasasel pinnal: N = m·g ≈ 5·9,81 = 49,05 N.
- Blokk massiga 2 kg kaldu tasandil nurga all θ = 30°: N = m g cosθ ≈ 2·9,81·cos30° ≈ 2·9,81·0,866 ≈ 16,98 N.
- Inimene liftis massiga 10 kg (näide): kui lift kiirendab üles a = 2 m/s², siis N = m(g + a) = 10·(9,81+2) = 118,1 N; kui lift kiirendab alla sama a, on N = 10·(9,81−2) = 78,1 N.
Kokkuvõte
Normaaljõud on pinnalt tulev kontaktjõud, alati pind- või suunaga risti. Lihtsaimal kujul on N = m·g lugedes tasast eset, kaldu pinnal N = m·g·cosθ, kuid reaalses olukorras tuleb arvestada kõigi normaalsuunaliste jõukomponentidega ja inertsimõjude (kiirenduste) mõjuga. Normaaljõud määrab oluliselt ka hõõrdumise suuruse ning seetõttu on see mehaanika ja igapäevaste probleemide lahendamisel keskne mõiste.
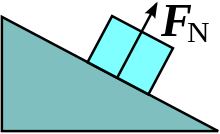
FN kujutab endast normaaljõudu
Küsimused ja vastused
K: Mis on normaalne jõud?
V: Normaaljõud on jõud, millega maapind (või mis tahes pind) tõukab tagasi üles.
K: Mis juhtuks, kui normaaljõudu ei oleks?
V: Kui normaaljõudu ei oleks, vajuksite aeglaselt maa sisse.
K: Kuidas on normaaljõud objektil seotud selle kaaluga?
V: Tasasel pinnal on objektile mõjuv normaaljõud võrdne tema massiga (objekti mass korrutatud raskusjõuga).
K: Kuidas mõjutab kaldus tasapind normaaljõudu?
V: Kaldtasapinnal väheneb normaaljõud nurga võrra ja seda saab arvutada, kasutades m g c o s θ.
K: Mida tähistab θ selles võrrandis?
V: θ tähistab selles võrrandis kaldenurka.
K: Millal oleks cosθ 1?
V: cosθ oleks 1, kui θ (nurk)on 0, mis esineb tasasel pinnal.
K: Kuidas on need kaks võrrandit omavahel võrreldavad? V: Need kaks võrrandit on võrdsed, kui nad asuvad tasasel pinnal.
Otsige