Snelli murdumisseadus — valguse murdumine, valem ja seletus
Snelli murdumisseadus: selge seletus, valem ja näited valguse murdumisest ning murdumisnäitajate seosest — Fermat'i tõestus ja praktilised rakendused.
Snelli murdumisseadus on teaduslik seadus valguse või muude lainete murdumise kohta. Optikas kirjeldab Snelli seadus, kuidas valguse suund muutub, kui laine läbib piirpinda kahe erineva keskkonna vahel (näiteks õhust klaasi). Seadus näitab, et langemisnurga (sissetuleva) ja murdumisnurga (väljamineva) siinuste suhe jääb konstantseks ning seda saab seostada laine kiiruse ja keskkondade murdumisnäitajatega:
sin θ 1 sin θ 2 = v 1 v 2 = n 2 n 1 {\displaystyle {\frac {\sin \theta _{1}}{\sin \theta _{2}}}={\frac {v_{1}}{v_{2}}}={\frac {n_{2}}{n_{1}}}} 
Tavapärasemalt väljendatakse Snelli seadust kujul n1 sin θ1 = n2 sin θ2, kus indeks 1 viitab sissetulevale keskkonnale ja indeks 2 väljaminevale keskkonnale. See kujul on sageli mugavam kasutada arvutusteks ja lihtsustab mõistmist: kui n kasvab, peab sin θ vähenema (st valgus murdub lähemale normaalile).
Muutujate tähendused ja ühikud
Iga θ {\displaystyle \theta } 
on nurk, mis on mõõdetud piirpinna normaalist (tagurpidi mõõtmine annaks sama seaduse). v {\displaystyle v}
on valguse kiirus vastavas keskkonnas (SI-ühikud on meetrit sekundis ehk m/s). n {\displaystyle n}
on keskkonna murdumisnäitaja (refractive index), mis iseloomustab, kuidas aine aeglustab valgust võrreldes vaakumiga.
Vaakumi murdumisnäitaja on 1 ja valguse kiirus vaakumis on c {\displaystyle c}
. Kui laine läbib materjali, mille murdumisnäitaja on n, muutub laine faasikiirus väärtusele c n {\displaystyle {\frac {c}{n}}}. 
. Samas sagedus f jääb piirpinna ületamisel muutumatuks, mistõttu lainepikkus λ muutub vastavalt λ = v / f.
Kriitiline nurk ja täielik sisepeegeldus
Kui valgus liigub optiliselt tihedamast keskkonnast (suurem n ehk näiteks klaas) hõredamasse keskkonda (väiksem n ehk näiteks õhk), võib esineda täielik sisepeegeldus. Selle juures määrab kriitiline nurk θc, mille korral murdumisnurk on 90° ja edasi ei pääse murdunud lainet välja:
- θc leiab avaldistest: sin θc = n2 / n1 (kehtib kui n1 > n2).
- Kui langemisnurk θ1 > θc, siis murdumisnurka ei teki ja kogu energia peegeldub tagasi — see on täielik sisepeegeldus.
Derivatsioon Fermat' printsiibist
Snelli seadust saab tõestada Fermat' printsiibi abil. Fermat' printsiip ütleb, et valgus liigub mööda teed, mis võtab kõige vähem aega. Kui analüüsida teekonda kahest punktist, mis on eraldatud piirpinnaga, ja leida ajafunktsiooni minimaalne väärtus, tekib tingimus, mis on täpselt Snelli seadus. See on elegantne optika ja analüütilise geomeetria seos.
Muud tähelepanekud ja laiem kontekst
- Lainepikkuse ja sageduse muutus: sagedus f jääb piirpinna ületamisel samaks, kuid lainepikkus muutub v = c/n ja seega λ = v / f väheneb optiliselt tihedamas keskkonnas.
- Dispersion: murdumisnäitaja n sõltub sagedusest (või lainepikkusest) — see nähtus, mida nimetatakse dispersiooniks, seletab näiteks valge valguse lahknemist prisma sees eri lainepikkusteks (vihmavarjude värvid).
- Kompleksne murdumisnäitaja: absorbeerivates meediumites on n komplekssed (n = n' + iκ), kus imaginaarne osa κ kirjeldab neeldumist.
- Fresneli valemid: Snelli seadus määrab murdumisnurga, kuid peegeldumise ja murdumise intensiivsuse sõltub ka polariseeritusest ning neid kirjeldavad Fresneli valemid.
Rakendused
Snelli seadus on praktiliselt kõigi optiliste seadmete ja tehnoloogiate aluseks:
- prismad ja läätsed (kujuliste kujunduste optimeerimine);
- optilised kiud (valguse juhtimine ja sisepeegeldus);
- mikroskoopia ja fotograafia (valguse suunamine ja fookustamine);
- lasersüsteemid ja spektroskoopilised seadmed.
Näide
Kui valgus liigub õhust (n1 ≈ 1,00) klaasi (n2 ≈ 1,50) ja langemisnurga θ1 = 30° korral, siis Snelli seaduse järgi:
n1 sin θ1 = n2 sin θ2 ⇒ sin θ2 = (n1 / n2) sin θ1 = (1,00 / 1,50) · sin 30° = (0,6667) · 0,5 = 0,3333, seega θ2 ≈ 19,5°.
Kokkuvõtteks: Snelli murdumisseadus annab lihtsa ja praktilise seose nurkade, lainekiiruse ja murdumisnäitajate vahel, võimaldades ennustada ja kujundada valguse käitumist erinevates materjalides.
Valguskiir tabab klaasprisma ja murdub.
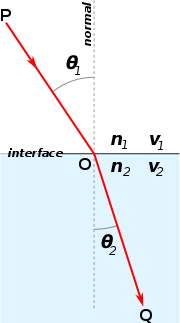
Valguse murdumine kahe erineva murdumisnäitajaga keskkonna vahelisel piiril, kus n2 > n1
Ajalugu
Sellel ideel on pikk ajalugu. Sellele probleemile pöörasid tähelepanu Aleksandria Hero, Ptolemaios, Ibn Sahl ja Huygens. Ibn Sahl avastas tegelikult murdumisseaduse. Huygens näitas 1678. aasta teoses "Traité de la Lumiere", kuidas Snelli siniseadust saab seletada valguse lainepõhisusega või tuletada sellest.
Küsimused ja vastused
K: Mis on Snelli murdumisseadus?
V: Snelli murdumisseadus on teaduslik seadus valguse või muude lainete murdumise kohta. Optikas sätestab see, et kui valgus läbib erinevaid materjale, ei muutu langus- ja murdumisnurkade siinuste suhe.
K: Kuidas saab Snelli seadust tõestada?
V: Snelli seadust saab tõestada Fermat' printsiibi abil, mis ütleb, et valgus liigub mööda teed, mis võtab kõige vähem aega.
K: Mis on Fermat' printsiip?
V: Fermat' printsiip ütleb, et valgus liigub mööda teed, mis võtab kõige vähem aega.
K: Mis on n ja v Snelli seaduses?
V: n on keskkonna murdumisnäitaja ja v on valguse kiirus vastavas keskkonnas (mõõdetuna meetrites sekundis).
K: Mida tähistab c Snelli seaduses?
V: c tähistab valguse kiirust vaakumis, mille murdumisnäitaja on võrdne 1.
K: Kuidas arvutatakse kiirust, kui laine läbib materjali, mille murdumisnäitaja on n?
V: Kiirus muutub c/n, kui laine läbib materjali, mille murdumisnäitaja on n.
Otsige