AlegsaOnline.com

Youngi topeltlõike katse: valguse laine-osakese duaalsus

Avasta Youngi topeltlõike katse ja valguse laine‑osakese duaalsus: selge ülevaade kvantmehaanikast, katse tulemused ja tähendus valguse ning elektronide käitumisele.

Autor: Leandro Alegsa

17-10-2025

Kvantmehaanika topeltlõike katse on füüsik Thomas Youngi poolt välja töötatud katse. See näitab, et valgusel on nii laine- kui ka osakeste iseloom ja et need on lahutamatud. Seega öeldakse, et valgusel on laine-osakese duaalsus, mitte ainult laine või ainult osake. Sama kehtib ka elektronide ja teiste kvantosakeste kohta.

Katse seadistus ja põhimõte

Lihtsustatult paigutatakse valgusallikas (näiteks laser) või elektronikiir kahe lähestikku oleva lõike (avatud) ette. Kui mõlemad lõigud on avatud, jõuab ekraanile nähtavale kohale interference ehk interferentsimuster — vahelduvad heledad ja tumedad triibud (fringed). See muster tekib seetõttu, et lainete tipud ja kõverused liituvad kas konstruktiivselt (heledad ribad) või destruktiivselt (tumedad kohad).

Tulemus ja miks see on oluline

Lainekäitumine: Kui valgus läbib mõlemad lõigud, käitub ta nagu laine, millel on faas ja amplituud — tulemuseks on interference-muster.
Osakese käitumine: Kui mõõdetakse, läbi kumma lõigu üksikosake (fotoni või elektroni) läks, kaob interference. Määramine (teadasaamine) annab osakeseomaduse ja „lainepilt“ hävib.
Duaalsus: Katse näitab, et valgusel (ja teistel kvantosakestel) ei saa rääkida ainult lainest või ainult osakesest — mõlemad omadused ilmnevad olenevalt eksperimendist.

Üksikfotonite ja üksikelektronite katsed

Kaasaegsed katsed lasevad üksikuid footoneid või elektrone läbi topeltlõike ühe kaupa. Kui üksikuid osakesi loendatakse ja kogutakse pikki aegu, tekib lõpuks sama interference-muster, mis tekiks laine puhul. See näitab, et iga üksikosake kirjeldub lainelise tõenäosuslainena (lainfunktsioon), mis levib mõlema lõigu kaudu kuni mõõtmise hetkeni.

Mõtestamine kvantmehaanikas

Topeltlõike katse illustreerib mitut keskset mõistet kvantmehaanikas:

Superpositsioon: Enne mõõtmist võib osake olla samaaegselt olukorras, kus ta on läbinud mõlemad lõigud (superponeeritud olek).
Mõõtmise roll: Kui üritatakse määrata «läbimisteed» (which-path info), puruneb superpositsioon ja interference kaob — seda kirjeldatakse sageli kui lainfunktsiooni kollapsi või dekoherentsust.
Komplementaarsus: N. Bohr’i põhimõte ütleb, et laineline ja osakelise kirjeldused on komplementaarsed: neid ei saa samaaegselt täielikult esile kutsuda ühe ja sama mõõtmise kaudu.

Matemaatiline lihtsustus

Interferentsi ribade vahelise kauguse (y) ja lõigute vahe (d), lainepikkuse (λ) ning ekraani kauguse (L) vahel kehtib lihtsustatud seos väikeste nurkade korral:

y ≈ λL / d

See aitab selgitada, miks ribade vahekaugus sõltub lainepikkusest: pikema lainepikkuse korral on ribad laiemalt eraldunud.

Ajalooline ja praktiline tähtsus

Thomas Young esitas oma katse tulemused 1801. aastal, pannes aluse laineoptika laiale tunnustusele. 20. sajandil sai see eksperiment oluliseks tõestuseks kvantteooria aluspõhimõtetele. Tänapäeval on topeltlõike katse oluline nii filosoofilises kui ka tehnilises mõttes: see aitab mõista kvantandmeid, kvantarvutuste alustõdesid, kvantsidet ja mõõtmise piire.

Kokkuvõte

Youngi topeltlõike katse on lihtne, ent sügav demonstratsioon sellest, et valgusel ja teistel kvantosakestel on nii laine- kui osakeseomadused. Katse rõhutab mõõtmise tähtsust kvantmaailmas ning näitab, et kvantobjektide käitumine sõltub eksperimentaalsest kontekstist — seetõttu on kvantmehaanikas keskne mõiste superpositsioon ja mõõtmisega seotud informatsioon.

Pilud; ülemiste postide vaheline kaugus umbes üks tolli.

Eksperiment

See katse on väga lihtne. Selleks on vaja ainult pildil kujutatud tüüpi topeltlõikeseadet, midagi, mis hoiab topeltlõikeseadet paigal, ja head laserit, nagu seda kasutavad töömehed ehitusel sirgete joonte "joonistamiseks". Laser on toetatud, nii et seda saab liigutada ainult meelega. See on suunatud kahe pilu vahelisse keskmisesse punkti umbes poole meetri kauguselt. Midagi nagu filmiekraan või sile valge sein pannakse teisele poole kahekordse pilu seadet mitme meetri kaugusele. Kui kõik on fikseeritud, ilmneb heledate ja tumedate ribade muster.

Laserid võivad toota ühe või mitu footonit, kui neile antakse teatud kogus elektrit. Fotoon või fotoonid väljuvad väga väikesest august teadaoleva aja jooksul. Valguse kiirus on teada, seega saab prognoosida, millal fotoonid ekraanile ilmuvad. Kui footonid tekivad ükshaaval, on ekraanil näha üksikuid valguslaike. Kui fotoonid oleksid lained, siis ootaksime, et nad leviksid liikudes laiali ja pudeneksid üle ekraani laia ala, kuid seda ei juhtu kunagi. Kui footonid oleksid osakesed, siis ootaksime, et nad ilmuksid ekraani kahes punktis, mis on ühendatud laseriga kahe keskel asuva pilu kaudu. Kuid ka seda ei juhtu.

Kui Thomas Young seda eksperimenti tegi, ei olnud tal laserit. Ta mõistis seda, kujutledes valgust kui veelaineid. Ta arvas, et valguslained liiguvad valgusallikast välja nagu lained, mis levivad tiiki langetatud kividest, ja et kui lainerinded tabavad kahekordset pilu, siis algne laine pääseb kahe pilu juures läbi ja sealt edasi on kaks erinevat lainet. Oli lihtne välja mõelda, kuidas kaks lainet suhtlevad, et tekitada ekraanil heledad ja tumedad ribad (mida sageli nimetatakse "ribadeks"). Ta ütles, et on tõestanud teooria, et valgus on lained.

Kuid seal olid suured probleemid. Valgus ei paistnud ekraanil lainetena, mis üle selle lainetasid. Valgust hakati mõistma kui fotoonide parve, mis ükshaaval avastamisekraani tabasid. Ja väga üllatavalt võis üks üksik fotoon interfereerida iseendaga, nagu oleks see üks laine, mis vastas vanale lainekirjeldusele. See jagunes kahekordse pilu seadme juures kaheks laineks, mis siis ekraanil ühinesid.

Sama seade, üks pilu avatud vs. kaks pilu avatud (märkige 16 riba).

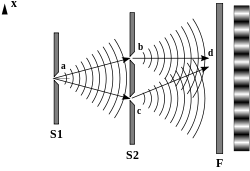
J on servade vaheline kaugus. J = Dλ/B "D" = dist. S2 kuni F, λ = lainepikkus, B = kaugus a kuni b

Tähtsus füüsika jaoks

Topeltlõike eksperiment sai klassikaliseks mõtteeksperimendiks, sest see selgitab selgelt kvantmehaanika keskseid mõistatusi.

Küsimused ja vastused

K: Mis on topeltlõike eksperiment?

V: Kvantmehaanika topeltlõheeksperiment on eksperiment, mille tegi esmakordselt füüsik Thomas Young 1801. aastal. See näitab, et valgusel on nii laine- kui ka osakese olemus ning et need olemusviisid on lahutamatud.

Küsimus: Kes viis esimesena läbi topeltkiirguse eksperimendi?

V: Topeltkiirguseksperimendi tegi füüsik Thomas Young esmakordselt 1801. aastal.

K: Mida näitab topeltkiirguse katse?

V: Topeltkiirguseksperiment näitab, et valgusel on nii laine- kui ka osakeste olemus ning et need on lahutamatud. Seega öeldakse, et valgusel on laine-osakese duaalsus, mitte ainult laine või ainult osakese olek. Sama kehtib ka elektronide ja teiste kvantosakeste kohta.

Küsimus: Kas valgus võib olla kas ainult laine või ainult osakese?

V: Ei, valgus ei ole võimalik olla kas ainult laine või ainult osakese; selle asemel on tal korraga nii lainete kui ka osakeste omadused - seda nähtust nimetatakse laine-osakese duaalsuseks. See kehtib ka elektronide ja teiste kvantosakeste kohta.

K: Millist tüüpi duaalsus on valgusel?

V: Valgusel on nn laine-osakeste duaalsus - see tähendab, et tal on korraga nii lainete kui ka osakeste omadused. See kehtib ka elektronide ja teiste kvantosakeste kohta.

K: Kas sama kehtib ka elektronide kohta?

V: Jah, sama põhimõte, mille kohaselt on korraga nii lainete kui ka osakeste omadused - mida nimetatakse "laine-osakeste duaalsuseks" - kehtib ka elektronide ja teiste kvantosakeste kohta.

K: Millal sai see nähtus tuntuks kui "laine-osakeste duaalsus"?

V: Laine-osakeste duaalsus sai laialdaselt aktsepteeritud pärast seda, kui Thomas Youngi 1801. aasta katsed kahekordse pilu katse abil näitasid, et valgusel on korraga nii lainete kui ka osakeste omadused.