Kõverate sobitamine: definitsioon, interpolatsioon, silumine ja regressioon

Kõverate sobitamine: õpi interpolatsiooni, silumist ja regressiooni praktiliselt — andmete modelleerimine, visualiseerimine ja usaldusväärne ekstrapoleerimine.

Autor: Leandro Alegsa

29-09-2025 14:51

Kõverate kohandamine on matemaatilise funktsiooni konstrueerimine, mis sobib kõige paremini andmepunktide kogumiga.

Kõverate kohandamine võib hõlmata kas interpolatsiooni või silumist. Interpolatsiooni kasutamine nõuab andmete täpset sobitamist. Tasandamise puhul konstrueeritakse "sileda" funktsiooni, mis sobib andmetele ligikaudselt. Sellega seotud teema on regressioonanalüüs, mis keskendub rohkem statistilise järeldamise küsimustele, näiteks kui palju on ebakindlust kõveras, mis on kohandatud juhusliku veaga vaadeldud andmetele.

Sobituskõveraid saab kasutada andmete visualiseerimise abiks, funktsiooni väärtuste arvamiseks, kui andmed puuduvad, ja kahe või enama muutuja vaheliste seoste kokkuvõtmiseks. Ekstrapoleerimine viitab kohandatud kõvera kasutamisele väljaspool vaadeldud andmete vahemikku. See on teatud määral ebakindel, sest see võib kajastada nii kõvera konstrueerimiseks kasutatud meetodit kui ka vaadeldud andmeid.

Peamised lähenemised

Interpolatsioon — eesmärk on leida funktsioon, mis läbib täpselt kõik andmepunktid. Levinud meetodid:

polünomiaalne interpolatsioon (Lagrange, Newton)
tükeldatud polünoomid ehk splines (eriti kuubiline spline)
rimestruktuurid (B-splines)

Interpolatsioon sobib, kui andmetel pole mõõtemüra ja soovitakse täpset läbitungimist. Tuleb olla ettevaatlik polünomiaalsete lähenemistega suure arvu punktide puhul — võib ilmneda Runge'i nähtus (võimsate polünoomide tugev lainetus servades).

Silumine (smoothing) — eesmärk on leida sile, üldistusvõimeline funktsioon, mis ei vasta täpselt iga punktile, vaid vähendab müra mõju. Levinud meetodid:

siluv splain (smoothing spline) — lisab tasakaalu sobituse ja kõverdumise vahel
LOESS / LOWESS — lokaalne regressioon, sobib mitteparametriliste sõltuvuste puhul
tugevusfiltrid ja liikuva keskmise meetodid
tuumapõhine (kernel) silumine

Silumist kasutatakse sageli eksperimentaandmete puhul, kus mõõteviga on märgatav ja eesmärk on leida üldine trend.

Regressioon — statistiline raamistik, kus huvi on ühenduse tugevuse ja usaldusväärsuse hindamine, sageli tingimusel, et andmed sisaldavad juhuslikku viga. Levinud variandid:

lineaarne regressioon ja mitmeregressioon
polünomiaalne regressioon (lineaarne sobitus polünomiaalsete tunnustega)
kaalutud ja robustne regressioon (vähendab outlierite mõju)
generaliseeritud lineaarmudelid (GLM), erinevate vähem tavapäraste vastustega

Regressioonis hinnatakse mudeli parameetrite ebakindlust (standardvead, konfidensivööndid) ja kasutatakse valikumeetmeid (AIC, BIC, ristvalideerimine) mudeli sobivuse hindamiseks.

Praktilised küsimused ja meetodivalik

Millist meetodit valida sõltub eesmärgist ja andmete omadustest. Mõned üldised juhised:

Kui andmed on täpsed: interpolatsioon (splines või täpne polünoom) võib olla sobiv.
Kui andmetel on müra: eelistada silumist või regressiooni, et vältida ülefitte.
Visualiseerimine ja trendide leidmine: LOESS, smoothing spline või madala järgu polünoomid annavad sageli selge tulemuse.
Etteaimamine väljaspool vahemikku: ekstrapoleerimine on riskantne; valida lihtsam, füüsikalisele teadmisele vastav mudel või kasutada hoiatusi.
Suured andmestikud: eelistada algoritme, mis on arvutuslikult efektiivsed (B-splines, lokaliseeritud meetodid, regulaarsed poli- või GLM-lahendused).

Olulised probleemid ja nende lahendused

Ülefitte ja alafitte: liiga keeruline mudel järgib müra (ülefitte), liiga lihtne ei püüdle olulisi mustreid (alafitte). Reguleerimise meetodid nagu ridge või lasso, samuti ristvalideerimine aitavad leida tasakaalu.

Numbrilised raskused: kõrge järgu polünoomid võivad olla ill-konditsioneeritud — eelistada stabiilsemaid baasfunktsioone (splines, ortogonaalsed polünoomid) või kasutada regulaarimist.

Runge'i nähtus: väldi ülemäära kõrge järgu polünoome ja kasuta tükeldatud polünoome (splines) või lokaalseid meetodeid.

Andmete ebaühtlane jaotumine ja sõlmpunktide valik: splainide puhul on sõlmpunktide (knots) paigutus oluline — neid saab valida fikseeritult, andmepõhiselt või optimeerida ristvalideerimise abil.

Hinnangud ja ebakindlus

Statistilises regressioonis hinnatakse mudeli sobivust ja parameetrite usaldusväärsust standardvigade, konfidensivööndite ning R² ja RMSE abil. Täpsemad usaldusvööndid kõvera kõigi punktide jaoks võimaldab saada nt kontrastide, funktsioonide standardvea analüüsi või bootstrapi abil. Siledate kõverate puhul saab määrata silumisparameetri (nt smoothing spline puhul lambda) ristvalideerimisega.

Rakendused

Kõverate sobitamine on laialt kasutusel:

füüsikas ja inseneriteadustes — eksperimentaalsed mõõtmised ja mudelite sobitamine
ökonomikas ja finantsanalüüsis — trendide ja tsüklite tuvastamine
bioloogias ja meditsiinis — kasvukõverad, dose–response mudelid
andmeteaduses — funktsioonide ligikaudistamine ja visualiseerimine suurte andmestike puhul

Kokkuvõttev nõuanded

Alusta lihtsast mudelist ja kasuta diagnostikat (jäägid, residuaalide muster), et otsustada keerukuse vajadus.
Kasuta ristvalideerimist mudeli valikul ja silumisparameetri häälestamisel.
Ole ettevaatlik ekstrapoleerimisel — paku alati usaldusvahemikke ja selgita piiranguid.
Kui eesmärk on statistiline järeldus, pöördu regressiooniliste ja probabilistlike meetodite poole; kui eesmärk on lihtsalt andmete täpne läbimine, võib interpolatsioon olla sobiv.

Kui soovid, võin lisada näiteid konkreetsete algoritmide (nt kuubiline spline, LOESS või least-squares lineaarregressioon) rakendamiseks populaarsetes programmeerimiskeeltes (R, Python) või koostada juhendi, kuidas hinnata sobivust ja valida parameetreid.

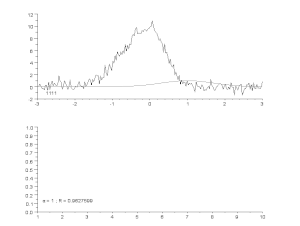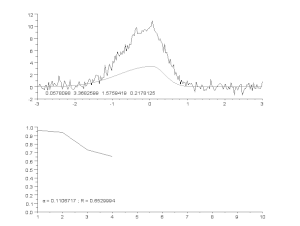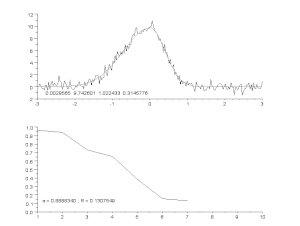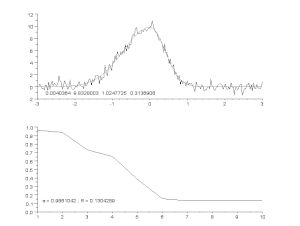
Mürase kõvera sobitamine asümmeetrilise tippude mudeli abil iteratiivse protsessi abil (Gauss-Newtoni algoritm muutuva summutusteguriga α). Ülemine osa: töötlemata andmed ja mudel. Alumine: vigade normaliseeritud ruutude summa areng.

Küsimused ja vastused

K: Mis on kõverus?

V: Kõverate sobitamine on protsess, mille käigus luuakse matemaatiline funktsioon, mis sobib kõige paremini andmepunktide kogumiga.

K: Milliseid kahte tüüpi kõverate sobitamist on?

V: Kõverate sobitamise kaks liiki on interpolatsioon ja silumine.

K: Mis on interpolatsioon?

V: Interpolatsioon on kõverate sobitamise liik, mis nõuab andmete täpset sobitamist.

K: Mis on silumine?

V: Silumine on kõverate kohandamise tüüp, mis konstrueerib "sileda" funktsiooni, mis sobib ligikaudselt andmetega.

K: Mis on regressioonanalüüs?

V: Regressioonanalüüs on sellega seotud teema, mis keskendub statistilise järeldamise küsimustele, näiteks sellele, kui suur on määramatus kõveras, mis on kohandatud juhusliku veaga vaadeldud andmetele.

K: Millised on mõned sobitatud kõverate kasutusalad?

V: Kohandatud kõverate abil saab andmeid visualiseerida, arvata funktsiooni väärtusi, kui andmed puuduvad, ja teha kokkuvõtteid kahe või enama muutuja vahelistest seostest.

K: Mis on ekstrapoleerimine?

V: Ekstrapoleerimine on kohandatud kõvera kasutamine väljaspool vaadeldud andmete vahemikku. See on siiski teatud määral ebakindel, kuna see võib kajastada nii kõvera konstrueerimiseks kasutatud meetodit kui ka vaadeldud andmeid.

Otsige