Funktsioon (matemaatika): definitsioon, domeen, kaasdomeen ja näited
Funktsioon (matemaatika): selge definitsioon, domeen ja kaasdomeen, intuitiivsed samm-sammulised näited ning praktilised selgitused algajatele ja edasijõudnutele.
Matemaatikas on funktsioon matemaatiline objekt, mis seob iga sisendi üheks väljundiks. Kui funktsioonile antakse sisend, siis see annab tagasi ühe (või mõnel üldistatud mõistel ka mitu) väljundit. Sisendid ja väljundid võivad olla näiteks arvud, vektorid või mis tahes elemendid mingis hulga sees.
Üldkõnekeeles saab funktsiooni ette kujutada kui masinat: masin võtab vastu väärtuse x ja tagastab väärtuse y. Kõigi võimalike x-väärtuste kogumit nimetatakse domeeniks. Kogumit, mis sisaldab kõiki väärtusi, mida y võiks teoreetiliselt saada (funktsiooni sihtruum), on artiklis esitatud linki järgnevalt nimetatud kaasvaldkonnaks. Oluline vahe on teha kaasdomeeni (sihtruumi) ja tegeliku pildi ehk funktsiooni väärtuste kogumi vahel: kõik pildis leiduvad elemendid kuuluvad kaasdomeeni, kuid mitte iga kaasdomeeni element ei pea olema funktsiooni tegelik väljund.
Kui y sõltub x-st vastavalt reeglile f, siis kirjutame y=f(x). Funktsiooni kolm osa — domeen, kaasdomeen ja seos — tähistatakse sageli notatsiooniga f : X → Y {\displaystyle f:X\to Y} 
(loe: "f on funktsioon X-st Y-ni"). See näitab, et funktsioon f võtab elemente hulgast X ja kuvab need hulka Y.
Lihtne näide on f(x)=x+1. Kui domeeniks on naturaalarvud x (0, 1, 2, 3, ...), siis vastavad väljundid y on samuti naturaalarvud ning y = x + 1 annab jada 1, 2, 3, 4, ...; seega on pilt (funktsiooni tegelik väärtuste hulk) kõik naturaalarvud alates 1-st. Originaalses näites on oluline eristada domeeni (kõik võimalused, mida x võib olla), kaasdomeeni (kõik võimalused, mida y võib teoreetiliselt olla) ja tegelikku pildi (mida f reaalselt võtab väärtuseks).
Mõned täpsemad mõisted
- Domeen (määramispiirkond) — hulk X, mille elementidele funktsioon on määratud.
- Kaasdomeen (sihtruum) — hulk Y, mille elemendid loetakse võimalikeks väljunditeks; kaasdomeeni ja pildi (image) erinevus on oluline.
- Pilt (image, väärtuste hulk) — alamhulk Y-st, mis koosneb kõigist tegelikest väljunditest f(x) funktsiooni kõigi x ∈ X korral.
- Presise määratluse järgi on funktsioon f hulgast X hulka Y määratlus, mis omistab igale x ∈ X täpselt ühe y ∈ Y.
Funktsioonide liigid lühidalt
- Injektsioon (üks-ühele) — funktsioon, kus erinevad sisendid annavad erinevad väljundid: kui f(x1)=f(x2), siis x1=x2.
- Surjektsioon (pealekaetav, täiskatte) — funktsioon, mille pilt võrdub kogu kaasdomeeniga Y; iga y ∈ Y on mõne x ∈ X kujutis.
- Bijektsioon — samaaegselt injektiivne ja surjektiivne funktsioon; sellisel juhul on olemas pöördfunktsioon f^{-1}: Y → X.
Operatsioonid funktsioonidega
- Koosseis: kahe funktsiooni f: X → Y ja g: Y → Z kooseis g ∘ f on funktsioon X → Z, mis määrab iga x ∈ X väärtuse g(f(x)).
- Pöördfunktsioon: olemas ainult bijektsioonide puhul; pöördfunktsioon f^{-1} annab iga y ∈ Y vastava x ∈ X.
- Eelkujutis (preimage): antud y väärtuse eelpilt on hulk {x ∈ X | f(x)=y}.
Veel näiteid
- f: R → R, f(x)=x^2 — domeen on kõik reaalarvud R ja kaasdomeen võib olla valitud R, kuid pilt on [0, ∞). Seetõttu pole see funktsioon surjektne R peale (kuna negatiivseid väärtusi ei anta).
- g: Z → Z, g(n)=2n — injektsioon (erinevad n annavad erinevad 2n), kuid ei ole surjektne kogu Z peale, sest näiteks 1 ei ole kujutis ühegi täisarvu korral; aga see on surjektne hulga kõigi paarisarvude suhtes.
Märkused ja soovitused
Funktsiooni mõiste on väga üldine: see ei pea olema alati antud lihtsa valemiga (võrrandiga). Funktsioon võib olla määratud tabeli, algoritmi, loogilise reegli või isegi keeruka geomeetrilise protsessina. Kui õpid funktsioone, keskendu esmalt mõistusele, et funktsioon määrab igale domeeni elemendile täpselt ühe väljundi — see on definitsiooni tuum.
Kui vaja, võin lisada illustratsioone, jooniseid või rohkem konkreetseid ülesandeid ja lahendusi, mis aitavad erinevaid funktsioonitüüpe paremini mõista.
Metafoorid
Tabelid
Sisendid ja väljundid võib panna tabelisse nagu pildil; see on lihtne, kui andmeid ei ole liiga palju.
Graafikud
Pildil on näha, et nii 2 kui ka 3 on paaritatud c-ga; see ei ole lubatud teises suunas, 2 ei saa väljastada c ja d,igal sisendil võib olla ainult üks väljund. Kõik f ( x ) {\displaystyle f(x)} 
(pildil c ja d) nimetatakse tavaliselt f {\displaystyle f}
kujutisekogumiks ja kujutisekogum võib olla kogu kaasvõrrand või mitte. Võib öelda, et kaasvaldkonna alamhulk A koos kujutisekogumiga on f(A). Kui sisendid ja väljundid on järjestatud, on neid lihtne graafikul kujutada:
Sel moel pilt tulevad pildi hulgast A. See teeb nii 2 ja 3 on paariline on ei ole lubatud teises suunas,isegi üks võib teha vahel codomain või mitte. Võib teha järelduse, et alamhulk A kaasvõrrand on kujutise hulk on F(A).
Ajalugu
1690. aastatel kasutasid Gottfried Leibniz ja Johann Bernoulli sõna funktsioon tähtede vahel, nii et tänapäevane mõiste sai alguse samal ajal kui arvutamine.
Aastal 1748 andis Leonhard Euler: "Muutuva hulga funktsioon on analüütiline väljend, mis koosneb mis tahes viisil muutuvast hulgast ja arvudest või konstantsetest suurustest." ja seejärel 1755: "Kui mõned suurused sõltuvad teistest suurustest nii, et kui viimaseid muudetakse, siis esimesed kogused muutuvad, siis nimetatakse esimesi suurusi viimaste funktsioonideks. See definitsioon kehtib üsna laialt ja hõlmab kõiki viise, kuidas üks suurus võib olla määratud teiste poolt. Kui seega x tähistab muutuvat suurust, siis nimetatakse kõiki suurusi, mis sõltuvad x-st mingil viisil või on sellest määratud, x-i funktsioonideks." mis on väga kaasaegne.
Tavaliselt omistatakse Dirichlet'ile versioon, mida kasutati koolides kuni 20. sajandi teise pooleni: "y on muutuja x funktsioon, mis on defineeritud intervallile a < x < b, kui igale muutuja x väärtusele selles intervallis vastab muutuja y kindel väärtus. Samuti on ebaoluline, mil viisil see vastavus on kindlaks tehtud."
1939. aastal üldistas Bourbaki Dirichlet' definitsiooni ja andis kogumiteteoreetilise versiooni definitsioonist kui sisendite ja väljundite vahelisest vastavusest; seda kasutati koolides umbes alates 1960. aastast.
Lõpuks 1970. aastal andis Bourbaki kaasaegse definitsiooni kui kolmik f = ( X , Y , F ) {\displaystyle f=(X,Y,F)} 
, kusjuures F ⊂ X × Y , ( x , f ( x ) ) ∈ F {\displaystyle F\subset X\times Y,(x,f(x))\ in F}
(st f : X → Y {\displaystyle f:X\to Y} ja F = ( ( x , f ( x ) ) | x ∈ X , f ( x ) ∈ Y } {\displaystyle F=\{(x,f(x))|x\in X,f(x)\in Y\}} 
).
Funktsioonide tüübid
- Elementaarfunktsioonid - funktsioonid, mida tavaliselt koolis õpitakse: murdud, ruutjuured, siinus, kosinus ja puutuja funktsioonid ning mõned muud funktsioonid.
- Mitteelemendilised funktsioonid - enamik neist ei kasuta operatsioone, mida me koolis ei õpi (nagu + või - või potensid). Paljud integraalid on mitteelementaarsed.
- Invertsed funktsioonid - funktsioonid, mis tühistavad teise funktsiooni. Näiteks: kui F(x) on funktsiooni f(x)=y pöördvõrrand, siis F(y)=x. Kõigil funktsioonidel ei ole inversioone.
- Erifunktsioonid: Funktsioonid, millel on nimed. Näiteks: siinus, kosinus ja puutuja. Funktsioone nagu f(x)=3x (kolm korda x) ei nimetata erifunktsioonideks. Need võivad olla elementaarseid, mitteelementaarseid või inversioone.
Küsimused ja vastused
K: Mis on matemaatikas funktsioon?
V: Funktsioon on matemaatikas objekt, mis annab väljundit, kui talle antakse sisend, mis võib olla arv, vektor või mis tahes asi, mis võib eksisteerida hulga sees.
K: Millised on kaks funktsioonidega seotud kogumit?
V: Kõigi väärtuste kogumit, mida x võib omada, nimetatakse domeeniks ja kogumit, mis sisaldab kõiki väärtusi, mida y võib omada, nimetatakse kaasdomeeniks.
K: Kuidas funktsioone sageli tähistatakse?
V: Funktsioone tähistatakse sageli kaldkirjas tähtedega, näiteks f, g, h.
K: Kuidas kujutatakse funktsiooni?
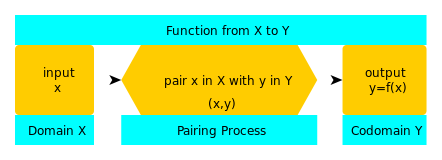
V: Me kujutame funktsiooni, kirjutades y = f(x), kus f on funktsiooni nimi ja kirjutatakse f : X → Y (funktsioon X-st Y-sse), et kujutada funktsiooni kolme osa - domeeni (X), kaasdomeeni (Y) ja paaritusprotsessi (nool).
Küsimus: Kas te oskate tuua näite funktsiooni kohta?
Vastus: Funktsiooni näide on f(x) = x + 1. Sisendiks antakse naturaalarv x ja saadakse naturaalarv y, mis on x + 1. Näiteks, kui anda f-le sisendiks 3, saadakse väljundiks 4.
Küsimus: Kas iga funktsioon peab olema võrrand?
V: Ei, mitte iga funktsioon ei pea olema võrrand. Funktsioonide põhiidee on see, et sisendid ja väljundid on kuidagi kokku pandud - isegi kui see võib olla väga keeruline.
Otsige