Hollandi skeemiteoreem: skeemid ja mõju geneetilistele algoritmidele

Hollandi skeemiteoreem selgitab, kuidas lühikesed kõrge sobivusega skeemid geneetilistes algoritmides eksponentsiaalselt levivad — mõju, tõlgendused ja kriitika.

Autor: Leandro Alegsa

20-10-2025 21:40

Hollandi skeemiteoreem, mida nimetatakse sageli ka geneetiliste algoritmide fundamentaalseks teoreemiks, on ebavõrdsus, mis tuleneb evolutsioonilise dünaamika jämedakujundamisest. Skeemiteoreem ütleb, et lühikesed, madalama astme skeemid (nn ehitusplokid), mille sobivus on üle keskmise, kipuvad järgnevatel põlvkondadel esinema sagedamini – vähemalt lootuspõhiselt ja mõningate eelduste korral. Teoreemi pakkus välja John 1970. aastatel ja algselt nähtigi selles seletust geneetiliste algoritmide võimele leida kompleksseid lahendusi; hiljem on selle tõlgendust ja piire laialdaselt arutatud. See tõlgendus on aga saanud kriitikat ning on näidatud, et skeemiteoreem on Price'i võrrandi erijuhtum, kus makroskoopilise mõõdupuuna kasutatakse skeemi indikaatorfunktsiooni.

Skeem (ingl schema) on mall, mis identifitseerib teatud bittstringide positsioonidel kindlaks määratud väärtustega sarnaste stringide alamhulga. Sageli kasutatav märgistus kasutab kolmeliikmelist tähistust {0,1,*}, kus tähega * tähistatakse tühist (wildcard) positsiooni. Skeemid on silindriliste kogude erijuht ja moodustavad seega topoloogilise ruumi — see on kasulik abstraktsioon, kui analüüsitakse, kuidas erinevad alarühmad populatsioonis muutuvad.

Formaalne kujutis ja tavapärane valem

Lihtsustatult väljendatakse skeemiteoreemi klassikaline ootusvõrrand järgmiselt (üldtuntud lähend):

E[m(H,t+1)] ≥ m(H,t) * (f(H) / f̄) * (1 - p_c * (d(H) / (l-1))) * (1 - p_m)^{o(H)}.

Siin tähistavad:

m(H,t) – skeemi H eksemplaride arv populatsioonis põlvkonnas t;
f(H) – nende eksemplaride keskmine sobivus (fitness);
f̄ – kogu populatsiooni keskmine sobivus;
p_c – crossover'i (ristumise) tõenäosus (tavaliselt eeldatakse ükepunktilist ristumist);
d(H) – skeemi määrav pikkus (defining length): indeksite vahe esimese ja viimase mitte-* positsiooni vahel);
l – kromosoomi pikkus (sõne pikkus);
p_m – mutatsiooni tõenäosus ühe bit'i kohta (bitwise mutation);
o(H) – skeemi aste (order): fikseeritud positsioonide arv.

Tõlge: kui skeem on lühike (väike d(H)) ja madala astmega (väike o(H)) ning selle keskmine sobivus on üle populatsiooni keskmise, siis eelduslikult kasvab selle esinemissagedus. Valemis on arvesse võetud kaks peamist hävitavat operatsiooni: ristumine (mis võib skeemi lõhkuda, sõltuvalt määravast pikkusest) ja mutatsioon (mis võib muuta fikseeritud positsioone).

Skeemide põhimõisted ja intuitsioon

Ehitusploki hüpotees: Holland ja paljud järgijad eeldasid, et geneetiline otsing töötab, liites kokku väikeseid, hea sobivusega ehitusplokke suuremateks lahendusteks. Skeemiteoreem tõlgendati selle hüpoteesi kvantitatiivseks toetuseks.
Oskuse ulatus: teoreem annab lõiduse (lower bound) oodatavale muutusele, mitte täpse ennustuse konkreetse jooksu kohta. See on lootuspõhine väide oodatava (expectation) käitumise kohta ja sõltub rangetest eeldustest (proportsionaalne valik, lihtne ristumine ja lihtne mutatsioonimudel).
Tõrjutused reaalses maailmas: lõplikud populatsioonid, stohhastilisus, sõltuvused geenide vahel (linkage), epistasis ja muud variandid ristumismeetoditest muudavad teoreemi praktilise jõu piiratumaks.

Piirangud ja kriitika

Skeemiteoreem ei taga, et head skeemid reaalselt kokku liidetakse või et need moodustavad globaalse optimi; see ütleb vaid, kuidas praegused head skeemid ootuspäraselt paljunevad. See ei selgita, kuidas sobivad skeemid kombineeruvad.
Hollandi algset tõlgendust on kritiseeritud selle üleliigse optimeerimise ja simplifikatsiooni pärast. Näiteks võib ristumine sagedasti hävitada kasulikke kombinatsioone, kui head geenikombinatsioonid asuvad erinevates kromosoomi piirkondades.
On näidatud, et skeemiteoreem on Price'i võrrandi erijuht — Price'i võrrand annab üldisema raamistikuga selgituse, kuidas keskmised fenotüübid/populatsioonisagedused muutuvad, ja skeemi indikaatorfunktsioon on üks võimalik makroskoopiline mõõde.
Kaasaegne uurimistöö rõhutab tihti linke õppe-meetodite ja tihendatud esitusviiside (nt seoseõppimine, populatsioonipõhised mudelid, estimatsioonipõhised algoritmid ehk EDA-d) tähtsust, mis võtab arvesse geenide omavahelist sõltuvust paremini kui lihtne skeemianalüüs.

Mõju geneetilistele algoritmidele ja praktilised järeldused

Praktilised nõuanded, mis tulenevad skeemiteoreemist:
- hoia ristumise tõenäosus ja esitusviis sellised, et kasulikud lähendused ei häviks kergesti;
- valikukomponent (selektiivsus) peab olema piisav, et soodsad skeemid paljunevad, ent mitte nii tugev, et hukkub mitmekesisus;
- mutatsioonimäärad peavad olema madalad, et vähendada paremike skeemide hävitamist, kuid piisavad, et võimaldada kohalikke variatsioone;
- arvestada tuleks kromosoomi kodeeringu ja geeni positsioneerimisega (linkage), sest head kombinatsioonid on lihtsam säilitada, kui need asuvad lähestikku.
Kuigi skeemiteoreem andis olulise teoreetilise aluse ja intuitiivse raamistikku, on tänapäeval sageli vajalik kombineerida seda kaasaegsete meetodite ja analüüsidega (nt Price'i võrrand, informatsiooniteooria ja statistilised mudelid), et paremini mõista ja juhtida geneetilise algoritmi käitumist keerukates ülesannetes.

Lihtne näide

Kujutame ette kromosoomi pikkust l = 10 ja skeemi H, mille aste o(H) = 2 ja määrav pikkus d(H) = 3. Kui m(H,t) = 10, f(H)/f̄ = 1.2, ristumise tõenäosus p_c = 0.6 ja mutatsioonitõenäosus p_m = 0.01, siis ligikaudne korrutegur, mis kirjeldab oodatavat kasvu, on:

(1.2) * (1 - 0.6 * (3/9)) * (1 - 0.01)^{2} ≈ 1.2 * (1 - 0.2) * 0.9801 ≈ 0.94.

See lihtsustatud arvutus näitab, et isegi kui skeemi keskmine sobivus on üle populatsiooni keskmise, võivad ristumine ja mutatsioon vähendada oodatavat kasvu — seega ei pruugi skeemi esinemissagedus tingimata kiiresti kasvada, eriti reaalses stohhastilises keskkonnas.

Kokkuvõtteks: Hollandi skeemiteoreem on oluline teoreetiline tulem, mis selgitab ühe vaatenurga alt, kuidas lühikesed madala astme, üle keskmise sobivusega skeemid kipuvad lootuspõhiselt paljunema. Kuid teoreemi piirangud ja eeldused teevad sellest pigem raamatusse matemaatilise tööriista kui otsese garantiini, et geneetiline algoritm alati "ehitusplokke" kombineerides optimaalse lahenduse leiab. Tänapäevane uurimistöö ühendab skeemianalüüsi laiemate teoreetiliste raamistikuga ning arvestab rohkem linke, epistasist ja populaatsioonipõhist struktuuri.

Kirjeldus

Vaatleme binaarsed stringid pikkusega 6. Skeem 1*10*1 kirjeldab kõikide stringide kogumit pikkusega 6, mille positsioonidel 1, 3 ja 6 on 1 ja positsioonil 4 on 0. * on jokersümbol, mis tähendab, et positsioonid 2 ja 5 võivad olla kas 1 või 0. Skeemi o ( H ) {\displaystyle o(H)} $o(H)$ järjekord on määratletud kui fikseeritud positsioonide arv šabloonis, samas kui defineeriv pikkus δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ on esimese ja viimase konkreetse positsiooni vaheline kaugus. Järjekord 1*10*1 on 4 ja selle defineeriv pikkus on 5. Skeemi sobivus on kõigi skeemile vastavate stringide keskmine sobivus. Stringi sobivus on kodeeritud probleemilahenduse väärtuse mõõt, mis arvutatakse probleemispetsiifilise hindamisfunktsiooni abil. Kasutades geneetiliste algoritmide väljakujunenud meetodeid ja geneetilisi operaatoreid, väidab skeemiteoreem, et lühikesed, madalama järjestusega skeemid, mille sobivus on üle keskmise, kasvavad järjestikuste põlvkondade jooksul eksponentsiaalselt. Väljendatuna võrrandina:

E ( m ( H , t + 1 ) ) ≥ m ( H , t ) f ( H ) a t [ 1 - p ] . {\displaystyle \operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p]. } $\operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p].$

Siin m ( H , t ) {\displaystyle m(H,t)} $m(H,t)$ on skeemi H {\displaystyle H} $H$ kuuluvate stringide arv põlvkonna t {\displaystyle t} juures. $t$ , f ( H ) {\displaystyle f(H)} $f(H)$ on skeemi H {\displaystyle H} $H$ täheldatud keskmine sobivus ja a t {\displaystyle a_{t}} $a_{t}$ on täheldatud keskmine sobivus põlvkonnas t {\displaystyle t} $t$ . Katkestuse tõenäosus p {\displaystyle p} $p$ on tõenäosus, et ristumine või mutatsioon hävitab skeemi H {\displaystyle H} $H$ . Seda saab väljendada järgmiselt:

p = δ ( H ) l - 1 p c + o ( H ) p m {\displaystyle p={\delta (H) \over l-1}p_{c}+o(H)p_{m}}} $p={\delta (H) \over l-1}p_{c}+o(H)p_{m}$

kus o ( H ) {\displaystyle o(H)} $o(H)$ on skeemi järjestus, l {\displaystyle l} $l$ on koodi pikkus, p m {\displaystyle p_{m}} $p_{m}$ on mutatsiooni tõenäosus ja p c {\displaystyle p_{c}} $p_{c}$ on ristumise tõenäosus. Seega on lühema määratluspikkusega δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ skeemi puhul väiksem tõenäosus, et see katkeb.
Tihti mõistetakse valesti, miks skeemiteoreem on ebavõrdsus, mitte võrdsus. Vastus on tegelikult lihtne: teoreem jätab tähelepanuta väikese, kuid mitte nullist tuleneva tõenäosuse, et skeemi H {\displaystyle H} $H$ kuuluv string luuakse "nullist" ühe stringi mutatsiooniga (või kahe stringi rekombinatsiooniga), mis eelmises põlvkonnas ei kuulunud skeemi H {\displaystyle H} $H$ . See tähendab, et skeemi H {\displaystyle H} ei ole võimalik luua.

Piirangud

Skeemiteoreem kehtib eeldusel, et geneetiline algoritm säilitab lõpmatult suure populatsiooni, kuid see ei kehti alati (piiratud) praktikas: algpopulatsiooni valimisvea tõttu võivad geneetilised algoritmid konvergeeruda skeemidele, millel puudub selektiivne eelis. See juhtub eelkõige multimodaalse optimeerimise puhul, kus funktsioonil võib olla mitu tippu: populatsioon võib triivida eelistama ühte tippu, ignoreerides teisi.

Põhjus, miks skeemiteoreem ei saa seletada geneetiliste algoritmide võimsust, on see, et see kehtib kõigi probleemiinstrumentide puhul ja ei suuda eristada probleeme, mille puhul geneetilised algoritmid töötavad halvasti, ja probleeme, mille puhul geneetilised algoritmid töötavad hästi.

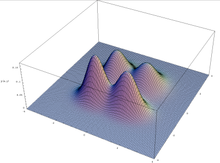
Multimodaalse funktsiooni graafik kahes muutujas.

Küsimused ja vastused

K: Mis on Hollandi skeemiteoreem?

V: Hollandi skeemiteoreem on geneetiliste algoritmide kohta käiv teoreem, mis ütleb, et keskmisest kõrgema sobivusega isendid on tõenäolisemad.

K: Kes ja millal pakkus välja Hollandi skeemiteoreemi?

V: John Holland esitas Hollandi skeemiteoreemi 1970. aastatel.

K: Mis on skeem geneetiliste algoritmide kontekstis?

V: Geneetiliste algoritmide kontekstis on skeem malli, mis identifitseerib stringide alamhulga, millel on sarnasused teatud stringipositsioonidel.

K: Kuidas tõlgendatakse Hollandi skeemiteooriat, mida kasutati geneetiliste algoritmide võimsuse selgitamise alusena?

V: Holland'i skeemiteoreemi tõlgendus, mida kasutati geneetiliste algoritmide võimsuse seletuste alusena, on see, et keskmisest kõrgema sobivusega isendid on tõenäolisemalt ülekaalus.

K: Mida on Holland'i skeemiteoreemi kriitika näidanud?

V: Hollandi skeemiteoreemi kriitika on näidanud, et see on Price'i võrrandi erijuhtum, mille makroskoopiline mõõtühik on skeemindikaatorfunktsioon.

K: Mis on silindriliste kogude erijuhtum?

V: Skeemid on silindriliste hulkade erijuhtum.

K: Millise ruumi moodustavad skeemid?

V: Skeemid moodustavad topoloogilise ruumi.

Otsige