Ebavõrdsus matemaatikas: tähendus, sümbolid ja näited
Ebavõrdsus matemaatikas: selgitused, peamised sümbolid ja praktilised näited. Lihtne juhend võrdluste mõistmiseks koos samm-sammuliste näidete ja harjutustega.
Ebavõrdsus on siis, kui üks objekt on:
- väiksem kui teine ( a < b {\displaystyle \ a<b} tähendab
, et a on väiksem kui b)
- suurem kui teine ( a > b {\displaystyle \ a>b} tähendab
et a on suurem kui b)
- ei ole väiksem kui teine ( a ≥ b {\displaystyle a\geq b}
tähendab, et a ei ole väiksem kui b, st ta on kas suurem või võrdne b-ga).
- ei ole suurem kui teine ( a ≤ b {\displaystyle a\leq b}
tähendab, et a ei ole suurem kui b või on väiksem või võrdne b-ga)
Ebavõrdsust kasutatakse mõnikord väite nimetamiseks, et üks avaldis on väiksem, suurem, mitte väiksem või mitte suurem kui teine.
Täiendavad märgid ja mõisted
- Range ehk lõplik ebavõrdsus: kasutusel on < ja >. Näide: 3 < 5 tähendab, et 3 on väiksem kui 5.
- Mitteilmeküllane (non-strict) ebavõrdsus: kasutusel on ≤ ja ≥. Näide: x ≥ 2 tähendab, et x võib olla 2 või mis tahes suurem väärtus.
- Võrdne olemine: märk on =.
- Erinev (mittevõrdne): kasutatakse märki ≠, mis tähendab, et kaks väärtust ei ole võrdsed.
Põhireeglid ebavõrduste töötlemiseks
- Kui liidad või lahutad mõlemalt poolt sama arvu, siis ebavõrdsuse suund ei muutu.
Näide: kui a < b, siis a + 3 < b + 3. - Kui korrutad või jagad mõlemalt poolt positiivse arvuga, ebavõrdsuse suund jääb samaks.
Kui a < b ja k > 0, siis ka k·a < k·b. - Kui korrutad või jagad mõlemalt poolt negatiivse arvuga, ebavõrdsuse suund pöördub.
Kui a < b ja k < 0, siis k·a > k·b. - Transitiivsus: Kui a < b ja b < c, siis a < c. Sama kehtib ≤ ja kombinatsioonide puhul (näiteks kui a ≤ b ja b < c, siis a < c või a ≤ c sõltuvalt olukorrast).
- Järjestatud ebavõrdsused: Võid kirja panna mitu ebavõrdsust koos: a < b ≤ c tähendab, et a on väiksem kui b ja b on ≤ c.
Kuidas esitada lahendit
Ebavõrdsuse lahendikogumit saab esitada mitmel viisil:
- Arvulise vahemiku vorm: näiteks x > 3 tähendab, et x kuulub vahemikku (3, ∞).
- Sulud ja kandilised sulud (intervalli notatsioon):
(a, b) tähendab a < x < b (a ja b ei kuulu hulka).
[a, b] tähendab a ≤ x ≤ b (a ja b kuuluvad hulka).
(a, b] ja [a, b) on kombineeritud variandid. - Graafiline esitus: numbrirealina — avatud ring (punkt) tähendab, et piirväärtus ei kuulu lahendisse, suletud ring tähendab, et kuulub.
Näited ja lahendused
- Lineaarne ebavõrdsus: lahenda 2x − 5 < 7.
2x < 12 ⇒ x < 6. Lahendihulk on (−∞, 6). - Negatiivse korrutise mõju: lahenda −3x ≥ 6.
Jagades −3-ga, tuleb ebavõrdsuse suund pöörata: x ≤ −2. Lahendihulk on (−∞, −2]. - Süsteem ebavõrdsustest: x > 1 ja x ≤ 4 ⇒ lahend on (1, 4]. See on kahe tingimuse lõike (ühine osa).
Praktilised tähelepanekud ja levinud vead
- Pöörake alati tähelepanu märgile, kui korrutate või jagate negatiivse arvuga — see on tavaline koht, kus tehakse viga.
- Kui ebavõrdsuse mõlemal pool on murdarvud või muutujad astmetega, siis olge tähelepanelik jagamise ja ruutjuurtega tegelemisel (nt ruutjuure võtmine nõuab, et arvestada mõlema poole võimalikku märki).
- Kui kasutate arvuti või kalkulaatoriga tööriistu, kontrollige alati lõppvastust käsitsi lühidalt — eriti kui tegemist on võrrandisüsteemidega või tingimustega, mis piiravad lubatud väärtusi (nt jagamine nulliga ei ole lubatud).
Lõppsõna
Ebavõrdsused on matemaatikas väga tähtsad nii teoorias kui rakendustes — need aitavad kirjeldada piirväärtusi, optimeerimisprobleeme ja tingimusi igapäevaelus (näiteks eelarved, mõõtuvõrdlused, temperatuuripiirid jms). Kui mõistate põhireegleid (liitmine, lahutamine, korrutamine, jagamine ja negatiivse korrutise mõju), siis on ebavõrdsuste töötlemine lihtsam ning turvalisem.
Töötamine ebavõrdsustega
Ebavõrdsus on matemaatikas see, kui kahte lahendust või vastust võrreldakse suuremate või väiksemate väärtustega. See on siis, kui kaks või veel palju lahendusi võrreldakse ei ole võrdse suurusega. Ebavõrdsuse lahendamine tähendab selle lahendite leidmist. Kui asendate arvu muutujale ja avaldis on tõene, siis on tegemist lahendiga. Kui asendate arvu muutujale ja väide ei ole tõene, siis ei ole see arv väite lahendus.
Ebavõrdsus on lahenduse leidmine antud muutujale. See on hulga suhtelise järjestuse leidmine. Ebavõrdsusel on palju lahendusi, kuid tuleb leida tegelikud lahendused. Ebavõrdsus on reaalarvude lahendamine. Ebavõrdsuse õige lugemisviis on vasakult paremale, nagu ka teiste võrrandite puhul, kuid ainus erinevus on see, et neil on iga võrrandi jaoks erinevad reeglid.
Näiteks x+4>12, kus x on reaalarv. Kõigepealt peab inimene leidma x ja ta peab teadma, kas see on lahendus. Vastus on x>8 ja see on õige väide. See avaldis käsitleb x-i asukohta reaalarvude kogumis. Arvujoon on üks võimalus näidata asukohta kõigi teiste reaalarvude suhtes (vt joonis Ebavõrdsus 1).
.jpg)
Ebavõrdsus 1 See on võrrandi x+4>12 lahendus.
Erinevad ebavõrdsused
On olemas viis erinevat liiki ebavõrdsust:
- Esimene neist on lineaarne ebavõrdsus, mis on ebavõrdsus, mis diferentseerib väljendeid kas väiksem kui või võrdne, väiksem kui või suurem kui või võrdne, suurem kui. See on üks, et kui me asendame ebavõrdsuse võrdsuse seosega, siis on tulemuseks lineaarne võrrand.
- Teine on ebavõrdsuste kombinatsioonid, mis on rahuldada ebavõrdsused, siis peab olema number lahenduskogumites nii, et arvud rahuldavad ebavõrdsused saavad olema väärtused kahe lahenduskogumi ristumisel.
- Kolmandaks on absoluutväärtustega seotud ebavõrdsused, mis tähendab, et väärtusi saab ümber sõnastada absoluutväärtustega seotud ebavõrdsuste kombinatsioonideks.
- Neljandat nimetatakse polünoomide ebavõrdsusteks, mis tähendab, et see on pidev, see tähendab, et nende graafikutel ei ole hüppeid ega katkestusi.
- Viimane, kuid mitte vähem tähtis, on ratsionaalne ebavõrdsus, mis tähendab, et see on ühe polünoomi jagatava polünoomi vorm. Teisisõnu, ratsionaalsete funktsioonide graafikud ei ole katkestusi ega esinda nimetaja nullidel.
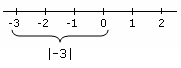
absoluutväärtus Näide, mis näitab absoluutväärtust
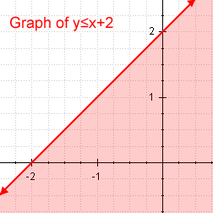
Lineaarne ebavõrdsus Näide lineaarse ebavõrdsuse kohta
Neli võimalust ebavõrdsuste lahendamiseks
Kvadraatiliste võrrandite lahendamiseks on neli võimalust:
- Reegel number üks on, et mõlemal pool tuleb lisada või lahutada sama arv.
- Reegel number kaks on see, et sa pead nihutama külgi ja muutma ebavõrdsuse märgi asukohta.
- Reegel number kolm on, et sa pead korrutama.
- Neljas reegel on jagada sama positiivne või negatiivne arv mõlemale poolele. Kuid neid saab kasutada ainult lihtsate ebavõrdsusprobleemide puhul.
Peale selle kulub ebavõrdsuse lahendamiseks kaks sammu. Esimene neist on lihtsustamine, kasutades liitmise või lahutamise pöördväärtust. Teine on lihtsustada rohkem, kasutades korrutamise või jagamise pöördväärtust. Kui te korrutate või jagate ebavõrdsuse negatiivse arvuga, siis pidage meeles, et pöörate ebavõrdsuse sümboli.

ebavõrdsuse korrutamise näide

Näide ebavõrdsuste liitmise kohta.
Näiteid ebavõrdsuste lahendamise kohta
Ebavõrdsus on matemaatiline avaldis, mis selgitab, et kaks väärtust ei ole võrdsed ja erinevad. Võrrand ab tähendab, et a ei ole võrdne b-ga. Ebavõrdsus on sama mis iga võrrand, kuid ainus erinevus on see, et ebavõrdsus ei kasuta võrdusmärki, vaid sümboleid. Ebavõrdsus b>a tähistab, et b on suurem kui a. Kiirusepiirangud,märk ja muud kasutavad ebavõrdsuse väljendamiseks.
Ebavõrdsuse lahendamisel peab inimesel olema tõene väide. Kui te jagate või korrutate ebavõrdsuse, mille mõlemal poolel on negatiivne arv, siis on väide vale. selleks, et väide oleks õige negatiivse arvuga, peate te selle väite õigeks muutmiseks pöörama sümboli ümber. Kui arv on positiivne arv, ei ole vaja sümbolit ümber pöörata. Ebavõrdsuse puhul on tegemist tõese väite tegemisega.
Alustage näiteks tõese väitega -6y<-12. Kui mõlemad pooled jagatakse -6-ga, saab tulemuseks y<2. Selles avaldises tuleb sümbol ümber pöörata, et saada tõeseks avaldiseks, y>2 on õige vastus. Arvjoonisel (vt joonis Ebavõrdsus 2) näitab suletud varjutatud ring, et see kuulub lahendikogumisse. Avatud ring näitab, et see ei kuulu lahenduskogumisse.
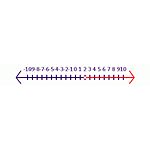
Ebavõrdsus 2 Lahendus võrrandile -6y<-12
Seotud leheküljed
- Võrdsus (matemaatika)
- Võrrand
Küsimused ja vastused
K: Mida tähendab "a < b"?
V: See tähendab, et a on väiksem kui b.
K: Mida tähendab "a > b"?
V: See tähendab, et a on suurem kui b.
K: Mida tähendab "a ≥ b"?
V: See tähendab, et a ei ole väiksem kui b, st ta on kas suurem või võrdne b-ga.
K: Mida tähendab "a ≤ b"?
V: See tähendab, et a ei ole suurem kui b või on väiksem või võrdne b-ga.
K: Kuidas saab ebavõrdsust matemaatikas kasutada?
V: Ebavõrdsust võib kasutada väite nimetamiseks, et üks avaldis on väiksem, suurem, mitte väiksem või mitte suurem kui teine.
Otsige