Parempoolne reegel — vektorite ristkorrutuse definitsioon ja juhend
Parempoolne reegel — selge definitsioon ja samm-sammuline juhend vektorite ristkorrutuse suuna mõistmiseks, praktilised näited ning visuaalsed nipid õppimiseks.
Parempoolne reegel on vektormatemaatika ja ruumilise geomeetria konventsioon, mis aitab meeles pidada ristprodukti (ristkorrutuse) suunda. Ristkorrutis a × b on vektor, mis on risti nii vektoritega a kui b ning mille pikkus on |a||b|sinθ (kus θ on kahe vektori vaheline nurk). Ristprodukti suunda määrab parempoolne reegel: see ütleb, kuidas pöidla, nimetissõrme ja keskmise sõrme asendid vastavad vektoritele ja nende ristkorrutisele. Lisateave suunda käsitleval lehel.
- Alustage, sulgedes oma parema käe ja sirutades välja oma nimetissõrme.
- Tõmmake pöial sirgelt üles, nagu teeksite relva märki.
- Kui suunate oma "relva" otse ette, siis sirutage keskmine sõrm välja nii, et see näitab vasakule ja kõik sõrmed on üksteise suhtes täisnurga all.
Kui teil on kaks vektorit, mida soovite ristkordistada, suunake pöial esimese vektori (a) suunas ja nimetissõrm esimese vektori suunas (b). Teie keskmine sõrm näitab ristprodukti a × b suunda. Oluline on järjekord: a × b on vastupidise suunaga võrreldes b × a; täpsemalt kehtib anti-kommutatiivsuse omadus b × a = −(a × b).
Olulised omadused ja tähelepanekud
- Pikkus: |a × b| = |a||b| sin θ. Kui vektorid on paralleelsed (θ = 0° või 180°), on ristkorrutis nullvektor.
- Suund: määratakse parempoolse reegliga (pöial → a, nimetissõrm → b, keskmine → a × b).
- Perpendikulaarne: a × b on risti nii a kui b-ga; seega (a × b) · a = 0 ja (a × b) · b = 0.
- Antikommutatiivsus: a × b = −(b × a).
Algebrailine valem kolmemõõtmelises koordinaatsüsteemis
Kui a = (ax, ay, az) ja b = (bx, by, bz), siis a × b = (ay bz − az by, az bx − ax bz, ax by − ay bx).
Lisaks füüsilisele sõrmeharjutusele kasutatakse ristkorrutist palju inseneriteadustes ja füüsikas (väärtuste nagu momendid, jõudude efektiivsed suunad, pöördemomendid jms leidmiseks). Pea meeles, et kui muudad vektorite ristkordistamise järjekorda, läheb tulemus vastupidises suunas. Seega on oluline veenduda, et te lähete järjekorras t h u m b → × p o i n t e r → = m i d d l e → {\displaystyle {\vec {thumb}\times {\vec {pointer}}={\vec {middle}}} 

Parempoolne reegel kruvikeermega toodetud liikumise kohta
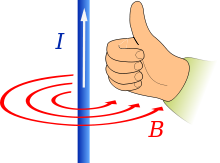
Välja (B) suuna ennustamine, kui vool I voolab pöidla suunas

Vasakpoolne orienteeritus on näidatud vasakul ja parempoolne paremal.
Variatsioonid
On veel üks reegel, mida nimetatakse parema käe haaramisreegliks (või korgitskruvi reegliks), mida kasutatakse magnetväljade ja pöörlevate asjade puhul.
1. Alustage, sirutades parema käe sirgelt välja ja suunates pöidla sirgelt välja, nii et see oleks teiste sõrmedega täisnurga all.
2. Nüüd keera sõrmed rusikasse ja hoia pöial väljas (nagu pöidlad üles).
3. Sobitage, kuidas teie sõrmed kõverduvad vastavalt sellele, kuidas miski liigub. Suund, kuhu teie pöial näitab, on vektori suund, mida me kasutame, et rääkida sellest.
Seda saab teha ka tagurpidi, alustades pöidlaga vektori suunas ja vaadates, kuidas sõrmed kõverduvad, et näha pöörlemissuunda. Kui suunate oma pöidla voolu suunas juhtmes, on magnetväli, mis selle ümber tekib, teie kõverduvate sõrmede suunas.
Küsimused ja vastused
K: Mis on parempoolne reegel?
V: Parema käe reegel on vektormatemaatikas kasutatav konventsioon, mis aitab meeles pidada suunda, kui vektorid ristkordistatakse.
K: Kuidas kasutada parema käe reeglit ristprodukti suuna väljaselgitamiseks?
V: Ristprodukti suuna väljaselgitamiseks sulgege oma parem käsi ja sirutage oma nimetissõrm välja. Pista pöial sirgelt üles, nagu teeksid sa püstoli märki. Suunake oma "püss" otse ette, siis sirutage keskmine sõrm välja nii, et see näitab vasakule ja kõik sõrmed on üksteise suhtes täisnurga all. Suunake pöidlaga esimese vektori suunas ja osutage näpuga teise vektori suunas. Teie keskmine sõrm näitab ristprodukti suunas.
K: Mis juhtub, kui te muudate järjekorda, kui vektorid ristkordistatakse?
V: Kui te vahetate järjekorda, kui vektorid ristkordistatakse, siis tulemus läheb vastupidises suunas. Seetõttu on oluline veenduda, et te lähete järjekorras pöidla x osuti = keskmine .
K: Mida see võrrand tähendab? {\displaystyle {\vec {thumb}\times {\vec {pointer}}={\vec {middle}}} .
V: See võrrand tähendab, et kui kaks vektorit ristatakse omavahel (pöial x osuti), siis saadakse kolmas vektor (keskmine).
Otsige