Young-Laplace'i võrrand
Füüsikas on Young-Laplace'i võrrand (/ləˈplɑːs/) mittelineaarne osaline diferentsiaalvõrrand, mis kirjeldab kahe staatilise vedeliku, näiteks vee ja õhu vahelist kapillaarrõhkude erinevust. See erinevus tuleneb pindpinevuse ehk seinapinevuse nähtusest. Seina pinget saab kasutada ainult väga õhukeste seinte puhul. Young-Laplace'i võrrand seostab rõhkude erinevust pinna või seina kujuga. See on väga oluline staatiliste kapillaarpindade uurimisel.
Füsioloogias on see tuntud kui Laplace'i seadus. Seda kasutatakse rõhu kirjeldamiseks õõnsate organite sees.
Võrrand on nime saanud Thomas Youngi järgi, kes töötas 1805. aastal välja pindpinevuse kvalitatiivse teooria, ja Pierre-Simon Laplace'i järgi, kes lõpetas matemaatilise kirjelduse järgmisel aastal. Mõnikord nimetatakse seda ka Young-Laplace'i-Gauss'i võrrandiks: Carl Friedrich Gauss ühendas 1830. aastal Youngi ja Laplace'i tööd. Gauss tuletas nii diferentsiaalvõrrandi kui ka piirtingimused, kasutades Johann Bernoulli virtuaalse töö põhimõtteid.
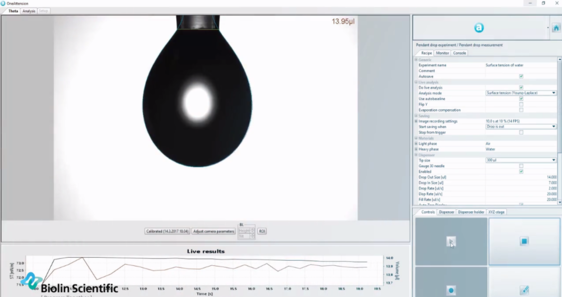
Optilised tensiomeetrid kasutavad Young-Laplace'i võrrandit, et määrata vedeliku pindpinevus automaatselt rippuvate tilkade kuju alusel.
Küsimused ja vastused
K: Mis on Young-Laplace'i võrrand?
V: Young-Laplace'i võrrand on mittelineaarne osaline diferentsiaalvõrrand, mis kirjeldab kapillaarrõhkude erinevust kahe staatilise vedeliku, näiteks vee ja õhu vahelisel piiril.
K: Millega on see seotud?
V: See seostab rõhkude erinevust pinna või seina kujuga.
K: Kes töötas selle teooria välja?
V: Teooria töötas välja Thomas Young 1805. aastal ja Pierre-Simon Laplace lõpetas selle matemaatilise kirjelduse järgmisel aastal. Hiljem ühtlustas selle 1830. aastal Carl Friedrich Gauss.
K: Kuidas seda kasutatakse füsioloogias?
V: Füsioloogias tuntakse seda Laplace'i seadusena ja seda kasutatakse õõnsate organite siserõhu kirjeldamiseks.
K: Millist nähtust see seletab?
V: Young-Laplace'i võrrand seletab pindpinevuse ehk seinapinevuse nähtust.
K: Kas seinapinevus kehtib paksude seinte puhul? V: Ei, seinapinevust saab kasutada ainult väga õhukeste seinte puhul.
