Ellips: definitsioon, geomeetria, valem ja omadused
Ellips: selge definitsioon, geomeetria, valemid ja omadused — intuitiivsed näited, fookused, võrrandid ning rakendused (orbiidid, konstruktsioonid)
Ellips on kumer tasandikõver, mis näeb välja nagu ovaal või lapik ring. Geomeetrias on ellips tasapinnaline kõver, mida saab saada ka koonuse ja tasapinna lõikumisel nii, et tekib kinnine kõver. Ring on ellipsi erijuhtum: kui ellipsi poolteljed on võrdsed (a = b), siis saame ringi. Ellipsi võib defineerida ka kui kõigi nende tasandi punktide asukohta, mille kauguste summa kahest fikseeritud punktist (fookustest) on konstantne.
Võrrand ja parameetrid
Keskpunkti (h,k) ümber joondatud ellipsi kanoniline võrrand on
(x - h)^2 / a^2 + (y - k)^2 / b^2 = 1
Siin eeldatakse tavaliselt, et a ≥ b > 0. Suurem pooltelg (major axis) on pikkusega 2a ja väiksem pooltelg (minor axis) pikkusega 2b. Vertikaal- või horisontaalse joondusega ellipsi tippudeks (vertex) on punktid
- (h ± a, k) — horisontaalse peateljega ellipsi tipud
- (h, k ± b) — vertikaalse peateljega ellipsi tipud
Fookused (foci) asuvad keskpunkist kaugusel c, kus
c = sqrt(a^2 − b^2) (kui a ≥ b). Horisontaalne ellipsi fookuste koordinaadid on (h ± c, k), vertikaalse peateljega ellipsi puhul (h, k ± c).
Alternatiivsed väljendid
- Nullpunkti ümber (h = 0, k = 0) keskne ellips: x^2/a^2 + y^2/b^2 = 1.
- Parametriline kujutis: x = h + a cos t, y = k + b sin t, t ∈ [0, 2π).
- Lokaatori definitsioon: ellips on punktide hulk, mille kahe fookuse kauguste summa on konstantne (täpsemalt 2a).
- Üldine kujutis tasandil: Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 on ellips siis, kui B^2 − 4AC < 0 (ja võrrand realiseerib kinnise kõvera).
Pindala, ümbermõõt ja muud valemid
- Pindala: A = πab.
- Ümbermõõt: ei ole elementaarset täpset suletud vormi; hea lähendus Ramanujanilt:
Per ≈ π [3(a + b) − sqrt{(3a + b)(a + 3b)}]. - Eksentrilisus: e = c / a, kus 0 ≤ e < 1; kui e = 0 siis ellips on ring (a = b).
Olulised omadused ja rakendused
- Peegeldusomadus: kiir, mis tuleb ühe fookuse suunalt ellipsile ja peegeldub, läbib teise fookuse — seda kasutatakse optikas ja akustikas.
- Stringi-ja-tihvti konstruktsioon: ellipsi saab joonistada kahe tihvti (fookuste) ja nööri abil — kirjelduse järgi kinnitatakse nöör fookuste ümber ning pingutatud nööri piki joonistatakse punktide trajektoor.
- Kõrgendused astronoomias: Kepleri seaduste järgi liiguvad planeedid päikese ümber ellipsikujulisel orbiidil, kus päike asub ühes fookuses.
- Affineerumine: ellips on ringi affiinselt muudetud kujutis (st ringi sirgjooneline teisendus annab ellipsi).
- Erijuht: ring on ellipsi erijuht, kus a = b ja mõlemad fookused langevad kokku keskpunktiga — seetõttu on ringil „üks keskpunkt”, kuid seda võib käsitleda ka kui ellipsi, millel fookused on kattuvad.
Kokkuvõtlikult: ellips on lihtne, kuid rikas geomeetriline kujund — sellel on selge analüütiline võrrand, tuntud geomeetrilised omadused (tippude ja fookuste asukohad, pindala, eksentrilisus) ning mitmesugused rakendused (optika, astronoomia, inseneriteadus). Fookus on ellipsi üks põhitähtsusega definitsioone, kuid ringi puhul need fookused langevad kokku keskpunktiga.
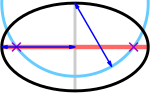
Fookused (lillad ristid) asuvad peatelje (punane) ja ringi (sinine), mille raadius on võrdne poolsuurteljega (sinine) ja mille keskpunkt on väike telg (hall), lõikepunktides.

Ellips, mis saadakse koonuse ja tasapinna lõikepunktina.
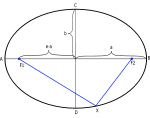
Ellips ja selle omadused.
Küsimused ja vastused
K: Mis on ellips?
V: Ellips on kuju, mis näeb välja nagu ovaal või lapik ring. Geomeetrias on see tasapinnaline kõver, mis tekib koonuse lõikumisel tasapinnaga nii, et tekib suletud kõver.
K: Kuidas luua ellips?
V: Ellipsi saab teha, kui panna kaks tihvti pappi ja seejärel panna nööri ümber nende kahe tihvti ning panna pliiats silmusesse ja tõmmata nii kaugele kui võimalik, ilma et nööri igas suunas murduks.
K: Mis on ringide erijuhtumid?
V: Ringid on ellipside erijuhtumid, mis tekivad siis, kui lõiketasand on risti koonuse teljega.
K: Mitu fookust on ellipsil?
V: Ellipsil on kaks fookust.
K: Milline võrrand kirjeldab ellipsi?
V: Ellipsi võrrand on (x - h)²/a² + (y - k)²/b² = 1, kus h ja k tähistavad ellipsi keskpunkti ja 2a tähistab pikkust pikema kõhnema külje mõlemast otsast, samas kui 2b tähistab pikkust lühema külje mõlema otsa vahel. C tähistab selle fookuste ja keskme vahelist pikkust, nii et A²-B²=C².
K: Kus näeme näiteid elliptiliste orbiitide kohta?
V: Elliptilisi orbiite võib näha planeetidel, mille ühes fookuspunktis on nende päike.
Otsige
