Ring (geomeetria): määratlus, raadius, läbimõõt, ümbermõõt ja pindala

Ring (geomeetria): selge määratlus, valemid ja näited — raadius r, läbimõõt d=2r, ümbermõõt C=2πr ja pindala A=πr². Õpi arvutama samm-sammult.

Autor: Leandro Alegsa

12-10-2025 16:13

Ring on ümmargune kahemõõtmeline kuju. Kõik punktid ringjoone serval on keskpunktist võrdsel kaugusel. Termin "ring" võib viidata kas ainult ringjoonele (ühemõõtmeline piir) ehk ringjoonele või sellele piirile vastavale täidetud kujule ehk piirkonnale (sage eestikeelne nimetus on ka "täidetud ring" või "ketas").

Kesktähised ja kujundi osad

Ringi keskpunkt on punkt, mis asub kujundi täpses keskmes. Raadius on joon, mis ühendab keskpunkti ja suvalist punkti ringjoonel; matemaatiliselt tähistatakse selle pikkust tavaliselt tähega r. Läbimõõt on sirgjoon, mis läbib keskpunkti ja ühendab kahte ringjoone punkti otse; selle pikkust tähistatakse tähega d ning kehtib seos d = 2r.

Ringi läbimõõt (mis tähendab "kogu ulatuses") on sirgjoon, mis kulgeb ühelt küljelt teisele ja otse läbi ringi keskme. Matemaatikud kasutavad selle joone pikkuse tähistamiseks tähte d. Ringi läbimõõt on võrdne kahekordse raadiusega (d võrdub 2 korda r).

d = 2 r {\displaystyle d=2\ r} $d=2\ r$

Ümbermõõt (ringjoone pikkus)

Ringi ümbermõõt on ringjoone ehk piirjoone pikkus. Seda tähistatakse tavaliselt suure tähega C. Ümbermõõdu ja raadiuse vahel kehtib oluline seos, kusjuures tähtsaks muutujaks on konstant π (pi):

Valemid: C = 2πr ja seega C = πd.
Ümbermõõdu ühik on pikkuse ühik (nt cm, m jne).

Arv π (pi)

Number π (kirjutatud kreeka tähega pi) on matemaatikas väga oluline konstant. See on ringjoone ümbermõõdu ja läbimõõdu suhe: π = C / d. Arv π on irratsionaalne (ei ole täpne murru kujul) ja ka transsendentne (ei ole ühegi polünoomi lahend). Ligikaudsed väärtused on näiteks murrud ²²/₇ (lihtne lähend) ja täpsem ³⁵⁵/₁₁₃, ning kümnendmuruna algab π ≈ 3,141592653589793....

Pindala

Piirkonna pindala (täidetud ringi pind) tähistatakse tavaliselt a või A. Pindala arvutatakse valemiga

A = π r² ehk pindala on võrdne π korda raadiuse ruuduga.
Alternatiivselt väljendatuna läbimõõdu kaudu: A = π d² / 4.

Pindala ühik on ruumalaühiku ruut (nt cm², m²).

Muud seotud valemid ja mõisted

Kaare pikkus: ringjoone osa pikkus (kaare pikkus) vastab valemile s = r θ, kus θ on kaare keskne nurk radiaanides.
Sectori pindala: sektori (tortu-kujuline osa) pindala on A_sector = 1/2 r² θ (θ radiaanides).
Rõngas (annulus): kujund, mis tekib kahe järjestikuse ringjoone vahelise ala puhul (sisemine raadius r, välimine R). Selle pindala on A = π (R² − r²).
Seos radiaanide ja kraadide vahel: täisring vastab 360° = 2π rad.

Näited

Kui raadius r = 3 cm, siis

läbimõõt d = 2r = 6 cm,
ümbermõõt C = 2πr ≈ 2·π·3 ≈ 18,85 cm,
pindala A = π r² ≈ π·9 ≈ 28,27 cm².

Märkused

Ringi ja sellega seotud mõistete tundmine on aluseks palju laiematele geomeetrilistele teemale — näiteks kõverjooneliste pindade, sektori- ja kaarearvutuste ning trigonometria põhivalemite mõistmisel. Ühtlasi on π arv, mille kümnendkohtade jada ei lõpe ega muutu perioodiliseks, mistõttu paljud ringiga seotud arvutused kasutavad ligikaudu väärtusi või sümboolset ekspressiooni π-ga.

Ring

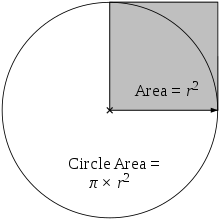
Ringi pindala on võrdne π-kordse halli ruudu pindalaga.

Arvutamine π

π saab mõõta, joonistades suure ringi ja mõõtes seejärel selle läbimõõtu (d) ja ümbermõõtu (C). Seda seetõttu, et ringi ümbermõõt on alati π-kordne läbimõõt.

π = C d {\displaystyle \pi =\frac {C}{d}} $\pi ={\frac {C}{d}}$

π saab arvutada ka ainult matemaatilisi meetodeid kasutades. Enamikul π väärtuse arvutamiseks kasutatavatest meetoditest on soovitavad matemaatilised omadused. Neid on aga raske mõista ilma trigonomeetriat ja arvutustehnikat tundmata. Mõned meetodid on aga üsna lihtsad, näiteks see Gregory-Leibnizi seeria vorm:

π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ⋯ {\displaystyle \pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\cdots } $\pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\cdots$

Kuigi seda rida on lihtne kirjutada ja arvutada, ei ole lihtne näha, miks see võrdub π-ga. Lihtsamalt mõistetavam on joonistada kujuteldav ring raadiusega r, mille keskpunkt on alguspunktis. Siis on iga punkt (x,y), mille kaugus d alguspunktist on väiksem kui r, arvutatuna pütagorase teoreemi järgi, selle ringi sees:

d = x 2 + y 2 {\displaystyle d={\sqrt {x^{2}+y^{2}}}} $d={\sqrt {x^{2}+y^{2}}}$

Ringi sees olevate punktide kogumi leidmine võimaldab hinnata ringi pindala A. Näiteks kasutades täisarvu koordinaate suure r puhul. Kuna ringi pindala A on π-kordne raadiuse ruut, siis saab π ligikaudselt arvutada, kasutades:

π = A r 2 {\displaystyle \pi ={\frac {A}{r^{2}}}} $\pi ={\frac {A}{r^{2}}}$

Seotud leheküljed

Sfäär

Küsimused ja vastused

K: Mis on ring?

A: Ring on ümmargune, kahemõõtmeline kuju. Kõik punktid ringi serval on keskpunktist ühesuguse kaugusega.

K: Mida kasutavad matemaatikud ringi raadiuse pikkuse tähistamiseks?

V: Matemaatikud kasutavad ringi raadiuse pikkuse tähistamiseks tähte r.

K: Mida kirjutatakse ringjoontes tähisega O?

V: Ringi keskpunkti kirjutatakse sageli tähega O.

K: Kui pikk on ringi läbimõõt?

V: Ringi läbimõõt (mis tähendab "kogu ulatuses") on sirge, mis läheb ühelt küljelt teisele ja otse läbi ringi keskpunkti. See on võrdne kahekordse raadiusega (d võrdub 2 korda r).

K: Millist tähte kasutavad matemaatikud ümbermõõdu tähistamiseks?

V: Matemaatikud kasutavad ümbermõõdu tähistamiseks tähte C, mis tähendab "ümberringi".

K: Kuidas saab arvutada pindala ringi sees?

V: Pindala A ringi sees saab arvutada, kui korrutada selle raadius iseendaga ja seejärel korrutada ً-ga (A võrdub ً korda r korda r).

Otsige