AlegsaOnline.com

Pythagorase teoreem – definitsioon, valem, tõestused ja näited

Põhjalik ja arusaadav juhend Pythagorase teoreemist: definitsioon, valem a²+b²=c², erinevad tõestused ja praktilised näited kiireks õppimiseks.

Autor: Leandro Alegsa

01-09-2025

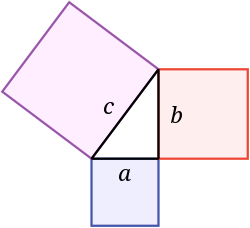
Matemaatikas on Pythagorase teoreem ehk Pythagorase lause väide täisnurkse kolmnurga külgede kohta.

Üks täisnurkse kolmnurga nurkadest on alati võrdne 90 kraadiga. See nurk on täisnurk. Kaks täisnurga kõrval asuvat külge nimetatakse jalgadeks ja teist külge nimetatakse hüpotenuusaks. Hüpotenuus on täisnurga vastaspool ja see on alati pikim külg.

Pythagorase teoreem ütleb lühidalt: hüpotenuusil asuva ruudu pindala on võrdne jalgade ruutude pindalade summaga. See teaduslik idee on nime saanud kreeka matemaatiku Pythagorase järgi, kuid sarnaseid teadmisi kasutati ka varasemates tsivilisatsioonides (näiteks babüloonlased ja Vana-India matemaatikud).

Kui jalgade pikkused on a ja b ning hüpotenuusa pikkus on c, siis a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}} $a^{2}+b^{2}=c^{2}$ . See on avaldus, mida saab tõestada paljude erinevate meetoditega.

Tõestuste kategooriad

Selle teoreemi kohta on palju erinevaid tõestusi. Neid võib üldiselt jagada nelja kategooriasse:

Geomeetrilised ümberpaigutused — pindalade ümberpaigutamise abil näidatakse, et hüpotenuusa ruudu pindala jaguneb täpselt jalgade ruutude pindalaks (nt Bhaskara ümberpaigutuse tõestus).
Sarnased kolmnurgad — kasutades täisnurkse kolmnurga ja selle kõrguse abil moodustuvaid sarnaseid kolmnurki, saab derivatsioonist lihtsa algebra abil välja tuua a² + b² = c² (seda meetodit kasutas ka Eukleidese stiilis tõestus).
Pindala- ja algebraalised tõestused — pindalade võrdlemine (nt ruut hüpotenuusa ümber ja neli kolmnurka ruudukooslusel) koos lihtsa algebra abil viib samale tulemile.
Analüütilised/vektor- ja koordinatsioonitõestused — koordinaatsüsteemis või vektoritega tõestades joonestatakse täisnurkne kolmnurk ja kasutatakse kauguse valemit (kõrgkooli analüüsist tuttav meetod).

Lühikesed tõestuse näited

Ümberpaigutuse (Bhaskara) idee: moodustage kahe sama suurusega täisnurkse kolmnurga abil suur ruut, milles jääb keskele ruut, mille külg on c. Arvutades sama kujundi pindala ka teisiti (neli kolmnurka + keskne ruut), saab algebra abil a² + b² = c².
Sarnaste kolmnurkade tõestus: täisnurkse kolmnurga kõrgus c küljele jagab kolmnurga kahte väiksemat sarnast kolmnurka; sarnasuse suhetest tulenevad proportsioonid annavad lõppkokkuvõttes a² + b² = c².
Koordinaattõestus: aseta täisnurkse kolmnurga tippudeks (0,0), (a,0) ja (0,b). Kaugus kahe tipu (a,0) ja (0,b) vahel on sqrt(a² + b²), mis on hüpotenuusa pikkus c — seega c² = a² + b².

Näited

Kolmnurk, mille jalgade pikkused on 3 ja 4: a² + b² = 3² + 4² = 9 + 16 = 25, seega c = 5. See on klassikaline Pythagorase kolmik 3–4–5.
Pythagorased triaadid: täisarvuliste külgedega täisnurkseid kolmnurki nimetatakse Pythagoraseks triaadideks. Üldine põlvkondamise valem (kui m>n>0, m ja n täisarvud, ei ole mõlemad paaritud ja gcd(m,n)=1) on:
- a = m² − n²,
- b = 2mn,
- c = m² + n².

Teoreemi pöördvõrdus ja üldistused

Pöördvõrdus: kui kolmnurga külgede puhul a² + b² = c², siis see kolmnurk on täisnurk (kus c on kõige pikem külg). See võimaldab kontrollida nurga sümmeetriat lihtsalt külgede pikkuste abil.
Kosinuseseadus: üldisemal kujul kolmnurga puhul kehtib kosinuseseadus: c² = a² + b² − 2ab cos(γ). Kui γ = 90°, siis cos(γ) = 0 ja saame Pythagorase valemi.
Ruumis ja mittelineaarsetes geomeetriates: Pythagorase lause kehtib eukleidilises ruumis. Mitte-eukleidilistes geomeetriates (siledal või hüperboolsel pinnal) üleminek on keerulisem ja tavaliselt ei kehti lihtsal kujul.

Rakendused

Pythagorase teoreemil on väga palju praktilisi rakendusi:

kauguse leidmine kahe punkti vahel koordinaatvõrgus (aritmeetiline geomeetria);
ehitus- ja inseneritööd (õige nurga ja kõrguse määramine);
trigonomeetria algtõed ja tasapinnaliste probleemide lahendamine;
arvutiteaduses graafika ja vektorite töötlus (pikima külje arvutamine, collision detection jm).

Pythagorase teoreem on üks matemaatika alustalasid: lihtne sõnastus, aga laialdane tähendus ja kasutus nii teoorias kui ka praktilistes probleemides.

Proof

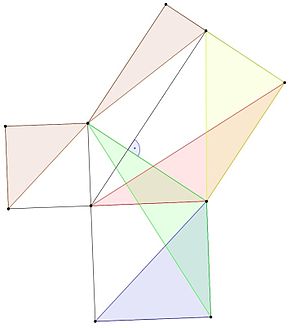
Ühe Pythagorase teoreemi tõestuse leidis kreeka matemaatik Eudoxus Cnidose matemaatik.

Tõendamiseks kasutatakse kolme lemmat:

Sama aluse ja kõrgusega kolmnurkadel on sama pindala.
Kolmnurgal, mille alus ja kõrgus on sama suur kui ruudu külg, on sama pindala kui pool ruudust.
Kolmnurgad, mille kaks külge ja üks nurk on kongruentsed, on kongruentsed ja neil on sama pindala.

See on tõestus:

Sinisel kolmnurgal on sama pindala kui rohelisel kolmnurgal, sest tal on sama alus ja kõrgus (lema 1).
Rohelise ja punase kolmnurga kaks külge on võrdsed sama ruudu külgedega ja nurk võrdne sirge nurgaga (90-kraadine nurk) pluss kolmnurga nurk, seega on nad kongruentsed ja neil on sama pindala (lemma 3).
Punase ja kollase kolmnurga pindalad on võrdsed, sest nende kõrgused ja alused on samad (1. laim).
Sinise kolmnurga pindala on võrdne kollase kolmnurga pindalaga, sest

A b l u e = A g r e e e n = A r e d = A y e l l o w {\displaystyle {\color {blue}A_{blue}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}} ${\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}$

Pruunid kolmnurgad on samadel põhjustel sama pindala.
Sinine ja pruun on kumbki poole väiksema ruudu pindalast. Nende pindalade summa on võrdne poole suurema ruudu pindalast. Seetõttu on väikeste ruutude pindalade pooled võrdsed suurema ruudu pindala poolega, seega on nende pindala võrdne suurema ruudu pindalaga.

Tõend sarnaste kolmnurkade abil

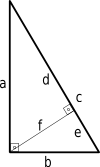
Saame Pythagorase teoreemi teise tõestuse, kasutades sarnaseid kolmnurki.

d a = a c ⇒ d = a 2 c ( 1 ) {\displaystyle {\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}\quad (1)} ${\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}\quad (1)$

e/b = b/c => e = b^2/c (2)

Pildi järgi teame, et c = d + e {\displaystyle c=d+e\,\! } $c=d+e\,\!$ . Ja asendades võrrandid (1) ja (2):

c = a 2 c + b 2 c {\displaystyle c={\frac {a^{2}}{c}}+{\frac {b^{2}}}{c}}}} $c={\frac {a^{2}}{c}}+{\frac {b^{2}}{c}}$

Korrutamine c-ga:

c 2 = a 2 + b 2 . \displaystyle c^{2}=a^{2}+b^{2}\,\!. } $c^{2}=a^{2}+b^{2}\,\!.$

Pythagorase kolmikud

Pythagorase kolmikud või kolmikud on kolm täisarvu, mis vastavad võrrandile a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}} $a^{2}+b^{2}=c^{2}$ .

Tuntud näide on kolmnurk, mille küljed on 3, 4 ja 5. Kui a=3 ja b=4, siis 3 2 + 4 2 = 5 2 {\displaystyle 3^{2}+4^{2}=5^{2}}} $3^{2}+4^{2}=5^{2}$ , sest 9 + 16 = 25 {\displaystyle 9+16=25}} $9+16=25$ . Seda saab näidata ka kui 3 2 + 4 2 = 5. {\displaystyle {\sqrt {3^{2}+4^{2}}=5.} ${\sqrt {3^{2}+4^{2}}}=5.$

Kolm-neli-viis-kolmnurk töötab kõigi 3, 4 ja 5 kordajate puhul. Teisisõnu on sellised arvud nagu 6, 8, 10 või 30, 40 ja 50 samuti Pythagorase kolmikud. Teine näide kolmiku kohta on kolmnurk 12-5-13, sest 12 2 + 5 2 = 13 {\displaystyle {\sqrt {12^{2}+5^{2}}}=13} ${\sqrt {12^{2}+5^{2}}}=13$ .

Pythagorase kolmikut, mis ei ole teiste kolmikute korrutis, nimetatakse primitiivseks Pythagorase kolmikuks. Iga primitiivne Pythagorase kolmik saab leida, kasutades väljendit ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})} $(2mn,m^{2}-n^{2},m^{2}+n^{2})$ , kuid peavad olema täidetud järgmised tingimused. Need seavad piirangud m {\displaystyle m} ja n {\displaystyle n} väärtustele.

m {\displaystyle m} ja n {\displaystyle n} on positiivsed täisarvud.
m {\displaystyle m} ja n {\displaystyle n} ei ole ühiseid tegureid peale 1
m {\displaystyle m} ja n {\displaystyle n} on vastupidise pariteediga. m {\displaystyle m} ja n {\displaystyle n} on vastupidise pariteediga, kui m {\displaystyle m} on paariline ja n {\displaystyle n} on paaritu või m {\displaystyle m} on paaritu ja n {\displaystyle n} on paariline.
m > n {\displaystyle m>n} .

Kui kõik neli tingimust on täidetud, siis moodustavad väärtused m {\displaystyle m} ja n {\displaystyle n} primitiivse Pythagorase kolmiku.

m = 2 {\displaystyle m=2} $m=2$ ja n = 1 {\displaystyle n=1} $n=1$ moodustavad primitiivse Pythagorase kolmiku. Väärtused vastavad kõigile neljale tingimusele. 2 m n = 2 × 2 × 1 = 4 {\displaystyle 2mn=2\times 2\times 1=4} $2mn=2\times 2\times 1=4$ , m 2 - n 2 = 2 2 - 1 2 = 4 - 1 = 3 {\displaystyle m^{2}-n^{2}=2^{2}-1^{2}=4-1=3} $m^{2}-n^{2}=2^{2}-1^{2}=4-1=3$ ja m 2 + n 2 = 2 2 + 1 2 = 4 + 1 = 5 {\displaystyle m^{2}+n^{2}=2^{2}+1^{2}=4+1=5} $m^{2}+n^{2}=2^{2}+1^{2}=4+1=5$ , seega tekib kolmik ( 3 , 4 , 5 ) {\displaystyle (3,4,5)} $(3,4,5)$ .

Küsimused ja vastused

K: Mis on Pythagorase teoreem?

V: Pythagorase teoreem on väide täisnurkse kolmnurga külgede kohta.

K: Milline nurk on täisnurkses kolmnurgas alati võrdne 90 kraadiga?

V: Üks täisnurkse kolmnurga nurkadest on alati võrdne 90 kraadiga, mida nimetatakse täisnurgaks.

K: Kuidas nimetatakse täisnurga kõrval asuvaid kahte külge?

V: Kaks täisnurga kõrval asuvat külge nimetatakse jalgadeks.

K: Kuidas nimetatakse täisnurga vastaspoolt?

V: Paralleelsele nurgale vastanduvat külge nimetatakse hüpotenuusaks ja see on alati pikim külg.

K: Kas selle teoreemi arvutamiseks on olemas võrrand?

V: Jah, selle teoreemi arvutamiseks on olemas võrrand, mis ütleb, et "hüpotenuusa pikkuse ruut on võrdne kahe teise külje pikkuste ruutude summaga".

K: Kas kõik kolmnurgad, mille nurk on 90-kraadine, loetakse "täisnurkseteks" kolmnurkadeks?

V: Ei, kõiki 90-kraadise nurgaga kolmnurki ei peeta "täisnurkseteks"; ainult neid, mille üks külg (hüpotenuus) on pikem kui kaks teist külge ja mille otsas on 90-kraadine nurk, võib liigitada "täisnurkseteks" kolmnurkadeks.