Pii (π) — matemaatiline konstant, ringi ümbermõõdu ja läbimõõdu suhe
Pii (π) — irratsionaalne matemaatiline konstant: ringi ümbermõõdu ja läbimõõdu suhe. Avastage tähendus, omadused, ajalugu ja praktilised näited lihtsas keeles.
Pi (või π) on matemaatiline konstant. See on ringi ümberringi kauguse ja ringi läbimõõdu suhe. See suhe annab ühe arvu ja see arv on alati sama — sõltumata ringi suurusest. Pi väärtus algab kui 3,14159265358979323846... ning jätkub lõputult ilma korduva mustrita. Selliseid numbreid nimetatakse irratsionaalseteks arvudeks.
Mis täpselt on läbimõõt ja ümbermõõt?
Läbimõõt on suurim akord, mis mahub ringi sisse; see läbib ringi keskpunkti. Ümberringi pikkust nimetatakse ümbermõõduks. Kuigi erinevatel ringidel on erinev läbimõõt ja erinev ümbermõõt, jääb nende suhe alati võrdseks arvuga π. Seega kehtib valem:
- ümbermõõt = π × läbimõõt
- või kuna läbimõõt d = 2r, siis ümbermõõt = 2πr
- ringi pindala = πr²
Arvuline väärtus ja lähendused
Pi on irratsionaalne ja ka transmendentaalne (st ei ole ühegi nullkoha polünoomi algebraalne arv). Tavapärane kümnendmurdne lähend on 3,14. Levinud murdlähendid on:
- 22/7 ≈ 3,142857 (lihtne lähend, kasutatakse sageli)
- 355/113 ≈ 3,14159292035 (väga täpne lühike murruümardus)
Arvulisi väärtusi on tänapäeval arvutatud miljoneid ja miljardeid komakohti kasutades efektiivseid algoritme (nt Chudnovsky algoritm). Pi täpne kümnendjärjestus ei kordu ega lõpe.
Matemaatilised omadused
- Irratsionaalsus: π ei ole esitatav kahe täisarvu jagatisena (proved 1761–1794 liikumises; esimene optimaalne tõestus Lambertilt 1768).
- Transcendentsus: Lindemann tõestas 1882. aastal, et π on transmendentaalne. See tõestus näitas ka, et kuupide ruudu parandamine ainult lõplike sammude abil (ehk "ruudu ruutmine") konstruktsiooniga joonlaua ja kompassiga on võimatu.
- Seosed teiste valemitega: pi esineb trigonomeetrias, kompleksanalüüsis (näiteks Euler'i valem e^{iπ} + 1 = 0), Fourier' analüüsis ja tõenäosusteoorias.
Ajalugu lühidalt
Inimestel on olnud huvi ringi ja selle omaduste vastu juba antiikajal. Vanaegiptuse ja Babüloonia käsikirjad sisaldavad lihtsaid lähendeid π‑le. Archimedes kasutas palju külgkontrolliga polügoone, et piirata π väärtust. Sümbol π hakkas laiemalt levima 1706. aastal, kui Walesi matemaatik William Jones kasutas seda esimestena ning see muutus rahvusvaheliselt tuntuks läbi Leonhard Euler'i tööde.
Arvutamise meetodid
Pi arvutamiseks on läbi ajaloo kasutatud mitmeid meetodeid:
- geomeetrilised meetodid (Archimedes: polügoonide lähenemine)
- liit- ja otsasarjad (nt Gregory–Leibniz seeria, kuid see on aeglane)
- kiired algoritmid ja komplekssed valemid (Machin‑tüüpi valemid, Gauss–Legendre, Chudnovsky jpt), mida kasutatakse arvutites miljardeid koma kohti saamiseks
Kasutusalad
Pi on fundamentaalne arv paljudes valdkondades:
- geomeetria ja trigonometria (ringid, sektorid, sihud)
- inseneriteadus ja fisika (võnkumised, laineprotsessid, ringjoonelised liikumised)
- statistika ja tõenäosusteooria (mõned tihedusfunktsioonid sisaldavad π‑d)
- kompleksanalüüs ja signaalitöötlus (Fourier' teisendused, e^{iθ} seos)
Kuigi π on tuntud kui ringi ümbermõõdu ja läbimõõdu suhe, ilmneb see arv ootamatult paljudes matemaatika ja loodusteaduste valdkondades ning selle uurimine on rikastanud nii teoreetilist kui rakenduslikku matemaatikat.
π = C d {\displaystyle \pi =\frac {C}{d}} 
(pi on võrdne ümbermõõdu jagatuna läbimõõduga).
Pi on lõputu numbrite jada
Lähenemine
Pii kirjutatakse sageli ametlikult π või kreeka täht π lühendina. Pi on ka irratsionaalne arv, mis tähendab, et seda ei saa kirjutada murdarvuna ( a b {\displaystyle a \over b}
), kus "a" ja "b" on täisarvud (täisarvud). See tähendab põhimõtteliselt seda, et pii kümnendmurdest paremal olevad numbrid lähevad igavesti, ilma et need korduksid mustris, ja et pii täpset väärtust on võimatu arvuna kirjutada. Pi saab ainult lähendada või mõõta väärtust, mis on praktilistel eesmärkidel piisavalt lähedane.
Pi lähedane väärtus on 3,141592653589793238462643... Tavaline pi-i lähendav murdarv on 22 7 {\displaystyle 22 \over 7}. 
, mis annab ligikaudu 3,14285714. See lähendus on 0,04% kaugusel pii tegelikust väärtusest. Kuigi seda lähendust kasutatakse enamasti reaalses elus, on murdarv 355 113 {\displaystyle 355 \over 113}
täpsem (annab umbes 3,14159292) ja seda võib kasutada, kui on vaja piile lähemal asuvat väärtust. Arvuteid saab kasutada pii paremaks lähendamiseks.
2019. aasta märtsis arvutas Emma Haruka Iwao pi väärtuse 31,4 triljoni numbrini.
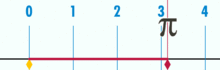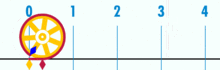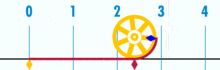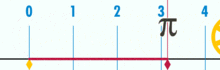
Joonis, mis näitab, kuidas π saab leida, kasutades ringi, mille läbimõõt on üks. Selle ringi ümbermõõt on π.
Ajalugu
Pi väärtust teadsid Vana-India matemaatikud nagu Bhaskaracharya ja Aryabhatta.
Matemaatikud on teadnud piid juba tuhandeid aastaid, sest nad on sama kaua töötanud ringidega. Nii vanad tsivilisatsioonid nagu babüloonlased on suutnud pii paljudele numbritele lähendada, näiteks murdosa 25/8 ja 256/81. Enamik ajaloolasi usub, et vanadel egiptlastel ei olnud π mõistet ja et vastavus on juhus.
Esimene kirjalik viide piile pärineb aastast 1900 eKr. Umbes 1650 eKr. andis egiptlane Ahmes Rhindi papüüruses väärtuse. Babüloonlased suutsid leida, et pii väärtus on veidi suurem kui 3, tehes lihtsalt suure ringi ja kleepides seejärel köie tüki ümbermõõdule ja läbimõõdule, märkides nende vahemaad ja jagades seejärel ümbermõõdu läbimõõduga.
Teadmised arvust pi jõudsid tagasi Euroopasse ja heebrealaste kätte, kes tegid selle arvu oluliseks Piibli Vana Testamendi osas. Pärast seda oli kõige tavalisem viis pii leidmiseks joonistada mõne ringi sisse paljude külgedega kuju ja kasutada selle kuju pindala pii leidmiseks. Kreeka filosoof Archimedes näiteks kasutas pii väärtuse leidmiseks 96 küljega hulknurga kuju, kuid hiinlased 500. aastal pKr suutsid pii väärtuse leidmiseks kasutada 16 384 küljega hulknurka. Kreeklased, nagu Anaxagoras Clazomenae, tegelesid ka muude ringi omaduste väljaselgitamisega, näiteks sellega, kuidas teha ringist ruutu ja arvuga pi ruutu. Sellest ajast alates on paljud inimesed püüdnud leida üha täpsemaid ja täpsemaid pii väärtusi.
| Pi ajalugu | ||
| Filosoof | Kuupäev | Lähenemine |
| umbes 150 CE | 3.1416 | |
| Zu Chongzhi | 430-501 EKR. | 3.1415929203 |
| al-Khwarizmi | umbes 800 CE | 3.1416 |
| al-Kashi | umbes 1430 | 3.14159265358979 |
| Viète | 1540-1603 | 3.141592654 |
| Roomen | 1561-1615 | 3.14159265358979323 |
| Van Ceulen | umbes 1600 | 3.14159265358979323846264338327950288 |
16. sajandil muutusid üha paremad ja paremad võimalused pii leidmiseks, näiteks Prantsuse jurist François Viète'i poolt välja töötatud keeruline valem. Kreeka sümbolit "π" kasutati esmakordselt William Jonesi 1706. aastal kirjutatud essees.
Matemaatik Lambert näitas 1761. aastal ka, et arv pi on irratsionaalne, st seda ei saa tavaliste standardite järgi kirjutada murdarvuna. Teine matemaatik nimega Lindeman suutis 1882. aastal näidata, et pi kuulub arvude rühma, mida nimetatakse transtsendentaalideks, mis on arvud, mis ei saa olla polünoomi võrrandi lahendus.
Pii saab kasutada ka paljude muude asjade arvutamiseks peale ringide. Pii omadused on võimaldanud seda kasutada paljudes teistes matemaatikavaldkondades peale geomeetria, mis uurib kujundeid. Mõned neist valdkondadest on kompleksanalüüs, trigonomeetria ja seeriad.
Pii tegelikus elus
Tänapäeval on olemas erinevaid viise, kuidas arvutada paljusid π-kohti. Sellest on aga piiratud kasu.
Mõnikord saab pii kasutada mis tahes ringi pindala või ümbermõõdu arvutamiseks. Ringi ümbermõõdu leidmiseks kasutage valemit C (ümbermõõt) = π korda läbimõõt. Ringi pindala leidmiseks kasutage valemit π (raadius²). Seda valemit kirjutatakse mõnikord järgmiselt: A = π r 2 {\displaystyle A=\pi r^{2}} 
, kus r on mis tahes ringi raadiuse muutuja ja A on selle ringi pindala muutuja.
Arvutada ringi ümbermõõt 1 mm veaga:
- 30 meetri raadiuse jaoks on vaja 4 numbrit.
- 10 numbrit Maa raadiusega võrdse raadiuse korral
- 15 numbrit raadiuse puhul, mis on võrdne Maa ja Päikese vahelise kaugusega.
Üldiselt tähistatakse 14. märtsi kui pii-päeva, sest 14. märtsi kirjutatakse ka kui 3/14, mis tähistab kolme esimest arvu 3,14 pii lähendamisel. Pi päev sai alguse 2001. aastal.
Seotud leheküljed
Küsimused ja vastused
K: Mis on arv ً?
V: ً on matemaatiline konstant, mis on ringi ümbermõõdu ja läbimõõdu suhe.
K: Mida see annab?
V: See annab arvu ja see arv on alati sama.
K: Kuidas see arv algab?
V: See arv algab kui 3,14159292653589793... ja jätkub lõputa.
K: Mis tüüpi numbrid need on?
V: Neid numbreid nimetatakse irratsionaalseteks arvudeks.
K: Mis on ringi läbimõõt?
V: Ringi läbimõõt on suurim akord, mis mahub ringi sisse, läbides selle keskkohta.
K: Mis on ringi ümbermõõt? V: Ümberringi pikkust nimetatakse ringi ümberringiks.
K: Kas pi jääb püsivaks sõltumata erinevatest ringidest? V: Jah, pi jääb erinevatest ringidest olenemata konstantseks, sest nende ümbermõõdu ja läbimõõdu suhe jääb alati samaks.
Otsige