Euler-Bernoulli talateooria definitsioon, põhimõtted ja rakendused

Euler-Bernoulli talateooria (tuntud ka kui inseneri talateooria või klassikaline talateooria) on lihtne ja laialdaselt kasutatav meetod talade paindumise arvutamiseks koormuse rakendamisel. See kehtib palgi väikeste läbipaindumiste (väikeste geomeetriliste deformatsioonide) korral ning eeldab, et nihke deformatsioonide (tõsise lõikepinda mõjutava nihke) mõju on ebaoluline. Seetõttu võib seda pidada Timošenko talateooria erijuhtumiks. Teooria algupära ulatub 18. sajandisse (umbes 1750. a) ning sai eriti tuntuks 19. sajandi lõpul, näiteks populaarsete konstruktsioonide nagu Eiffeli torn ja Ferris'i ratas arendamise ajal. Pärast seda on seda kasutatud paljudes tehnikavaldkondades, sealhulgas masinaehituses ja tsiviilehituses. Kuigi on olemas täpsemaid meetodeid, kasutatakse Euler–Bernoulli teooriat selle lihtsuse ja piisava täpsuse tõttu paljudes praktilistes ülesannetes.

Põhimõtted ja peamised eeldused

Materjal on lineaarne ja elastsusõiguspärane (Hooke’i seadus kehtib): pinge on proportsionaalne nihkega.
Risti lõikepinnad jäävad painduva talaga kokku «tasasteks» ja püsivad painutamisel risti neutraaltelje suhtes (ristsed lõiked ei kurru ega paindu eraldi).
Lõikepindade jäämine risti neutraaltelje suhtes tähendab, et lõikejooneline nihke deformatsioon (shear) on vähetähtis — seega nihke deformatsioonid jäetakse sageli arvestamata.
Talad on „õhukesed” ehk pikkus on oluliselt suurem kui ristlõike mõõtmed (slender beam), ja läbipaindumised on väikesed nii, et lineaarsed lähenemised kehtivad.

Põhivõrrand (diferentsiaalvõrrand)

Euler–Bernoulli talavõrrand õhukese talapõhimõtte korral on neljanda järgu diferentsiaalvõrrand:

E I d⁴w/dx⁴ = q(x)

kus E on Young’i moodul, I on ristlõike teine moment (inertsusmoment), w(x) on talale tekkiv vertikaalne läbipaindumine, ja q(x) on joonekoormus (jõu jagunemine pikkuse ühiku kohta). Selle võrrandi lahendamiseks lisatakse sobivad piirtingimused (kinnitused, vabad otsad jms).

Pinge-, momendi- ja paindevõrrandid

Paindemoment M(x) on seotud kõverusega: M(x) = -E I d²w/dx².
Bendingu (painde) normaalpinged ristlõikes (lähtuvalt neutraaltelje kaugusest y): σ(x,y) = - (M(x)·y) / I. Või asendusena σ = -E·y·d²w/dx².

Levinud lahendusjuhud ja näited

Cantilever (klamber ühe otsa külge) koos punktkoormaga P vabastipulisel otsal: tipu läbipaindumine δ = P L³ / (3 E I).
Lihtsasti toetatud tala (simply supported) keskkoormuse P korral: maksimaalne läbipaindumine keskpunktis δ = P L³ / (48 E I).

Need lihtsad valemid annavad kiire hindamise ja on tavapärane osa konstrueerimise kontrollidest.

Piirangud ja millal kasutada Timoshenko teooriat

Euler–Bernoulli teooria eeldab, et lõikekiirendus (shear deformation) on ebaoluline. Kui tala jäikus lõikes on väike või tala on lühike ja jäme (madal pikkus/ügavus suhe), võivad nihkest tingitud deformatsioonid märkimisväärselt mõjutada vastust — sellisel juhul on parem kasutada Timoshenko talateooriat, mis lisab lõikevenituse ja pöördemassi mõju.
Kõrgusvibratsioonide (suure sagedusega dünaamilised probleemid), suured geomeetrilised muutused (suur defleksioon) või mitte-lineaarsed materjaliomadused nõuavad edasiarendusi, mitte klassikalist Euler–Bernoulli lähenemist.
Komposiitmaterjalide, mitte-prismaatiliste ristlõigete ja keerukate ühenduste puhul tuleb hoolikalt hinnata teooria kehtivust või kasutada numbrilisi meetodeid (näiteks FEM).

Rakendused

Euler–Bernoulli talateooriat kasutatakse laialdaselt:

ehitiste ja sildade elementide esmaseks arvutuseks, talade ja väntvõllide koormustanalüüsiks;
masinaosade (vardad, tugitalad, raamid) projekteerimisel;
õppetöös ja praktilise inseneritöö kiiretes hinnangutes;
näitajana, mille abil hinnata, kas on vaja edasiarendusi (näiteks Timoshenko või täis-3D FEM) keerukamate mudelite jaoks.

Lühike ajalooline märkus

Teooria arendati 18. sajandil Leonhard Euler’i ja Jakob Bernoulli panuste tulemusena ning sai laialdase kasutuse 19. sajandi tööstusrevolutsiooni ja suurte konstruktsioonide rajamisel. Selle selgus ja lihtsus on muutnud selle praktiliseks tööriistaks nii teoreetilisele insenerile kui ka praktiseerijale.

Euler–Bernoulli talateooria ei ole kõikvõimas, kuid tänu oma lihtsusele, selgetele eeldustele ja sageli piisavale täpsusele on see inseneripraktikas endiselt väga oluline tööriist.

Vibreeriv klaaspalk, mis näitab talade paindumist, mida saab hinnata Euler-Bernoulli talateooria abil.

Ajalugu

Leonhard Euler ja Daniel Bernoulli panid selle teooria esimesena kokku 1750. aastal. Tollal suhtuti teadusse ja inseneriteadusesse teisiti kui tänapäeval. Matemaatilisi teooriaid, nagu Euleri-Bernoulli talateooria, ei usaldatud praktilise inseneripraktika jaoks. Sildade ja ehitiste projekteerimisel kasutati samu meetodeid kuni 19. sajandi lõpuni. See on aeg, mil Eiffeli torn ja Rikeratas näitasid teooria paikapidavust suuremates mõõtkavades.

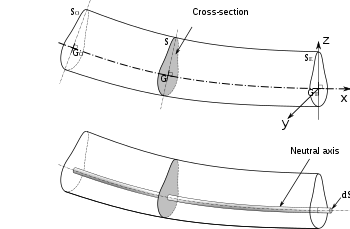
Joonis painutatud palgi ristlõike kohta, millel on näidatud neutraaltelg

Staatilise tala võrrand

Euler-Bernoulli võrrand kirjeldab tala läbipainde ja rakendatud koormuse vahelist seost järgmiselt:

d 2 d x 2 ( E I d 2 w d x 2 ) = q {\displaystyle {\frac {\mathrm {d} ^{{2}}{\mathrm {d} x^{2}}}\left(EI{\\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}\right)=q\,} ${\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\left(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}\right)=q\,$

Kus w ( x ) {\displaystyle w(x)} $w(x)$ kirjeldab palgi läbipaistet z {\displaystyle z} $z$ suunas mõnes kohas x {\displaystyle x} . q {\displaystyle q} on jaotatud koormus, teisisõnu jõud pikkusühiku kohta (analoogiliselt rõhu kui jõu kohta pindala kohta); see võib olla funktsiooniks x {\displaystyle x} , w {\displaystyle w} . $w$ või muudest muutujatest.

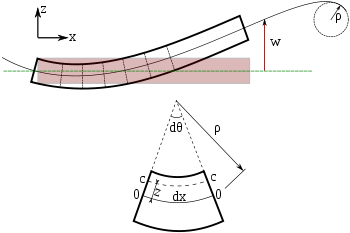
Euler-Bernoulli palgi painutamine. Tala iga ristlõige on neutraaltelje suhtes 90-kraadise nurga all.

Küsimused ja vastused

K: Mis on Euler-Bernoulli kiirteooria?

V: Euler-Bernoulli talateooria on lihtne meetod, mida kasutatakse talade paindumise arvutamiseks koormuse rakendamisel, arvestamata nihke deformatsioonide mõju.

K: Millal võeti Euler-Bernoulli talateooria esmakordselt kasutusele?

V: Euler-Bernoulli talateooria võeti esmakordselt kasutusele umbes 1750. aastal.

K: Kas Euler-Bernoulli talade teooriat kasutati Eiffeli torni ja Ferris'i ratta arendamisel?

V: Jah, Euler-Bernoulli palgiteooria sai populaarseks Eiffeli torni ja Ferris ratta arendamisel 19. sajandi lõpus.

K: Millistes tehnikavaldkondades on Euler-Bernoulli palgiteooriat kasutatud?

V: Euler-Bernoulli talade teooriat on kasutatud paljudes tehnikavaldkondades, sealhulgas masinaehituses ja tsiviilehituses.

K: Kas Euler-Bernoulli palgiteooriat kasutatakse tänapäevalgi laialdaselt?

V: Jah, Euler-Bernoulli talateooriat kasutatakse tänapäevalgi laialdaselt selle lihtsuse tõttu, kuigi on välja töötatud ka teisi täiustatud meetodeid.

K: Millist tüüpi talade läbipaindumise suhtes kehtib Euler-Bernoulli talateooria?

V: Euler-Bernoulli tala teooria kehtib tala väikeste läbipaindumiste puhul.

K: Kas Euler-Bernoulli talateooria võtab arvesse ka nihke deformatsioonide mõju?

V: Ei, Euler-Bernoulli talateooria ei võta arvesse nihke deformatsioonide mõju.