Lineaarregressioon
Lineaarne regressioon on viis selgitada sõltuva muutuja ja ühe või mitme selgitava muutuja vahelist seost sirgjoone abil. See on regressioonanalüüsi erijuht.
Lineaarne regressioon oli esimene regressioonianalüüsi tüüp, mida uuriti põhjalikult. Seda seetõttu, et mudeleid, mis sõltuvad lineaarselt nende tundmatutest parameetritest, on lihtsam sobitada kui mudeleid, mis on oma parameetritest mittelineaarselt sõltuvad. Lisaks sellele on saadud hinnangute statistilisi omadusi lihtsam määrata.
Lineaarsel regressioonil on palju praktilist kasutust. Enamik rakendusi kuulub ühte kahest järgmisest laiast kategooriast:
- Lineaarset regressiooni saab kasutada prognoositava mudeli kohandamiseks vaadeldud väärtuste (andmete) kogumile. See on kasulik, kui eesmärk on ennustamine, prognoosimine või vähendamine. Kui pärast sellise mudeli väljatöötamist antakse seejärel täiendav väärtus X ilma sellega kaasneva väärtuseta y, saab sobitatud mudelit kasutada y väärtuse ennustamiseks.
- Arvestades muutujat y ja mitmeid muutujaid X1, ..., Xp, mis võivad olla seotud y-ga, saab lineaarset regressioonanalüüsi rakendada, et kvantifitseerida y ja Xj vahelise seose tugevust, hinnata, millised Xj ei ole üldse seotud y-ga, ja tuvastada, millised Xj alamhulgad sisaldavad üleliigset teavet y kohta.
Lineaarsete regressioonimudelite puhul püütakse teha joone ja andmepunktide (nt jääkide) vaheline vertikaalne kaugus võimalikult väikeseks. Seda nimetatakse "joone sobitamiseks andmetele". Sageli püütakse lineaarsete regressioonimudelite puhul minimeerida jääkide ruutude summat (vähimad ruutud), kuid on olemas ka teisi sobitamise viise. Nende hulka kuulub "sobivuse puudumise" minimeerimine mõnes muus normis (nagu vähimate absoluutsete kõrvalekallete regressioonis) või vähimate ruutude kadumisfunktsiooni karistatud versiooni minimeerimine, nagu ridge-regressioonis. Väikseimate ruutude meetodit saab kasutada ka selliste mudelite sobitamiseks, mis ei ole lineaarsed. Nagu eespool kirjeldatud, on mõisted "vähimad ruutud" ja "lineaarne mudel" tihedalt seotud, kuid need ei ole sünonüümid.
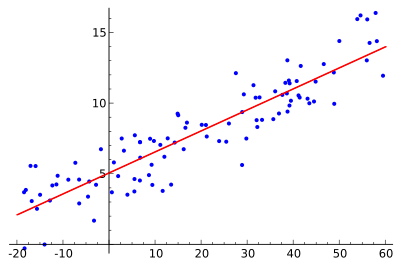
Idee on leida punane kõver, sinised punktid on tegelikud proovid. Lineaarse regressiooniga saab kõik punktid ühendada ühe sirgjoonega. Selles näites kasutatakse lihtsat lineaarset regressiooni, kus punase joone ja iga proovipunkti vahelise kauguse ruutu minimeeritakse.
Kasutamine
Majandus
Lineaarne regressioon on peamine analüüsivahend majandusteaduses. Näiteks kasutatakse seda tarbimiskulutuste, püsiinvesteeringute kulutuste, varuinvesteeringute, riigi ekspordi ostude, impordikulutuste, likviidsete varade nõudluse, tööjõunõudluse ja tööjõupakkumise prognoosimiseks.
Küsimused ja vastused
K: Mis on lineaarne regressioon?
V: Lineaarne regressioon on viis, kuidas vaadata, kuidas midagi muutub, kui teised asjad muutuvad, kasutades matemaatikat. See kasutab sõltuvat muutujat ja ühte või mitut selgitavat muutujat, et luua sirgjoon, mida nimetatakse "regressioonijooneks".
K: Millised on lineaarse regressiooni eelised?
V: Mudeleid, mis sõltuvad lineaarselt oma tundmatutest parameetritest, on lihtsam sobitada kui mudeleid, mis on oma parameetritest mittelineaarselt sõltuvad. Lisaks on saadud hinnangute statistilisi omadusi lihtsam määrata.
K: Millised on lineaarse regressiooni praktilised kasutusalad?
V: Lineaarset regressiooni saab kasutada prognoositava mudeli sobitamiseks vaadeldavatele väärtustele (andmetele), et teha prognoose, prognoose või vähendamisi. Seda saab kasutada ka muutujate vaheliste seoste tugevuse kvantifitseerimiseks ja selliste andmete alamhulkade kindlakstegemiseks, mis sisaldavad üleliigset teavet mõne teise muutuja kohta.
K: Kuidas püütakse lineaarsete regressioonimudelite abil vähendada vigu?
V: Lineaarsed regressioonimudelid püüavad teha vertikaalset kaugust joone ja andmepunktide (jääkide) vahel võimalikult väikeseks. Seda tehakse kas jääkide ruutude summa (väikseimad ruudud), sobimatus mõne muu normi (väikseimad absoluutsed kõrvalekalded) või väikseima ruutude kadumisfunktsiooni karistatud versiooni (ridge regressioon) minimeerimise teel.
Küsimus: Kas on võimalik, et lineaarse regressiooni mudelid ei põhine vähimatel ruutudel?
V: Jah, on võimalik, et lineaarsete regressioonide mudelid ei põhine vähimad ruutude meetodil, vaid kasutavad selle asemel selliseid meetodeid nagu sobimatuse puudumise minimeerimine mõnes muus normis (vähimad absoluutsed kõrvalekalded) või vähimad ruutude kadude funktsiooni karistatud versiooni (ridge regressioon) minimeerimine.
Küsimus: Kas "lineaarne mudel" ja "vähimad ruutud" on sünonüümid?
V: Ei, need ei ole sünonüümid. Kuigi need on omavahel tihedalt seotud, viitab "lineaarne mudel" konkreetselt sirgjoone kasutamisele, samas kui "vähimad ruutud" viitab konkreetselt sellele, et püütakse minimeerida vigu, tagades, et sirgjoone ja andmepunktide vahel on minimaalne vertikaalne kaugus.
