Nomogramm
Nomogramm ehk joondusgraafik ehk abaque, on graafik arvutamiseks. See on kahemõõtmeline diagramm, mis annab matemaatilise funktsiooni arvutuse.
Nomograafia leiutas 1884. aastal prantsuse insener Philbert Maurice d'Ocagne (1862-1938). Seda kasutati aastaid selleks, et võimaldada inseneridele keeruliste valemite kiireid graafilisi arvutusi. Nomogrammid kasutavad d'Ocagne'i leiutatud paralleelset koordinaatsüsteemi, mitte tavalisi kartesiaanlikke koordinaate.
Nomogramm koosneb n-st skaalast, millest iga muutuja kohta on üks võrrandis. Teades n-1 muutuja väärtusi, saab leida tundmatu muutuja väärtuse või mõne muutuja väärtuste fikseerimise teel uurida fikseerimata muutujate vahelist seost.
Tulemus saadakse, kui asetada joonlaud üle teadaolevate väärtuste skaalal ja lugeda tundmatu väärtus sealt, kus see ületab selle muutuja skaala. Joonlaua abil loodud virtuaalset või tõmmatud joont nimetatakse indeksjooneks või isopletiks.
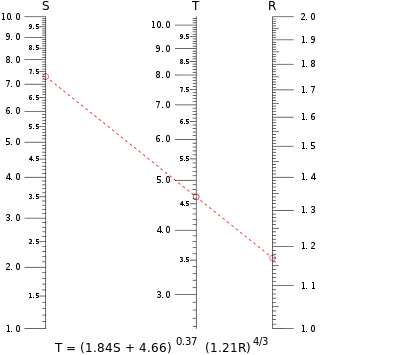
Tüüpiline paralleelskaala nomogramm. Selles näites arvutatakse T väärtus, kui S = 7,30 ja R = 1,17 asendatakse võrrandisse. Isotüüp ületab T skaala veidi alla 4,65.
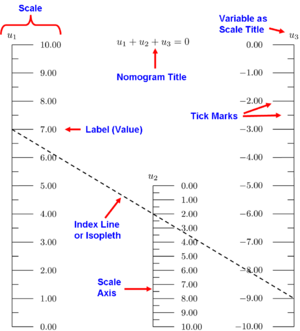
Paralleelskaala nomogrammi komponendid
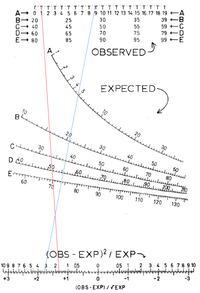
Chi-ruutude jaotuse nomogramm
Kasutage
Nomogramme kasutati laialdaselt umbes 75 aastat. Need võimaldasid kiireid ja täpseid arvutusi enne taskukalkulaatorite ajastut. Nomogrammi tulemused saadakse kiiresti ja usaldusväärselt ühe või mitme joone tõmbamisega. Kasutaja ei pea tulemuste saamiseks oskama lahendada algebralisi võrrandeid, otsida andmeid tabelitest, kasutada tõkkepuudust või asendada numbreid võrranditesse. Kasutaja ei pea isegi teadma nomogrammi aluseks olevat võrrandit.
Nomogrammide kujundamisel on arvesse võetud valdkondlikke teadmisi. Näiteks suuremate nomogrammide loomiseks suurema täpsuse saavutamiseks hõlmab nomograaf tavaliselt ainult mõistlikke ja probleemi jaoks huvipakkuvaid skaalaulatusi. Paljud nomogrammid sisaldavad muid kasulikke tähistusi, nagu võrdlusmärgised ja värvilised piirkonnad. Kõik need pakuvad kasutajale kasulikke suunaviitasid.
Nomogramm on sarnaselt joonlaual põhinev graafiline analoogarvutusseade. Sarnaselt joonlaual on selle täpsus piiratud täpsusega, millega füüsilisi märke saab joonistada, reprodutseerida, vaadata ja joondada.Joonlaud on üldotstarbeline arvutusarvuti, kuid nomogramm on mõeldud konkreetsete arvutuste tegemiseks. Nomogramme saab siiski kasutada teise, täpsema, kuid võimalike vigadega seotud arvutuse vastuse kontrollimiseks.
Küsimused ja vastused
K: Mis on nomogramm?
V: Nomogramm on arvutamiseks kasutatav graafik, mis annab matemaatilise funktsiooni arvutuse.
K: Kes leiutas nomograafia?
V: Nomograafia valdkonna leiutas 1884. aastal Prantsuse insener Philbert Maurice d'Ocagne.
K: Mis oli nomogrammide eesmärk?
V: Nomogramme kasutati aastaid selleks, et inseneridele pakkuda keeruliste valemite kiireid graafilisi arvutusi.
K: Mitmest skaalast koosneb nomogramm?
V: Nomogramm koosneb n-st skaalast, millest iga muutuja kohta võrrandis on üks.
K: Kuidas saab tundmatu muutuja väärtuse leida nomogrammi abil?
V: Teades n-1 muutuja väärtusi, saab tundmatu muutuja väärtuse leida, asetades joonlaua üle skaalade teadaolevate väärtuste ja lugedes tundmatu väärtuse sealt, kus see ületab selle muutuja skaala.
K: Kuidas nimetatakse sirgjoonega loodud virtuaalset või tõmmatud joont?
V: Sirgjoonlaua abil loodud virtuaalset või joonistatud joont nimetatakse indeksjooneks või isopletiks.
K: Millist koordinaatsüsteemi kasutatakse nomogrammides?
V: Nomogrammides kasutatakse d'Ocagne'i poolt leiutatud paralleelset koordinaatsüsteemi, mitte tavalisi kartesiaanlikke koordinaate.
