Arvutuslükati (slaidireegel) – mehaaniline analoogarvuti ja kasutus
Arvutuslükati (slaidireegel) tutvustus, mehaaniline analoogarvuti ja kasutus korrutamiseks, jagamiseks, logaritmid, trigonomeetria, ajalooline taust ja spetsiaalrakendused lennunduses ning rahanduses
Slipstick ehk arvutuslükati või slaidireegel on mehaaniline analoogarvuti, mis võimaldab teha kiireid ja täpseid ligikaudseid arvutusi ilma elektrita. Tõkkepulka kasutatakse peamiselt korrutamiseks ja jagamiseks, aga ka "teaduslikeks" funktsioonideks, näiteks juurte, logaritmide ja trigonomeetria jaoks. Tavapäraste skaalaehituste tõttu ei sobi slaidireegel otse liitmiseks või lahutamiseks, kuid keerukamate protseduuridega saab neid operatsioone samuti teostada mõnevõrra ebatavalisemate meetoditega.
Kuidas slaidireegel töötab
Slaidireegel kasutab logaritmide omadust, et korrutamine vastab logaritmiliste pikkuste liitmisele: kahe arvu logaritmid liites saadakse korrutise logaritm. Seade koosneb tavaliselt kolmest osast: fikseeritud kere ehk raam (stock), liikuv lüli (slide) ja indikaator (cursor või hairline) – peenikese joonega aknaga liikuva klaasist või metallist osa, mis näitab täpseid skaala-asendeid.
Skaalad ja tähised
Arvutuslükati pinnal on mitu standardset skaalat (nt C, D, A, B, CI, K, L, S, T), mis on paigutatud vastavalt funktsioonile. Näiteks:
- C ja D – põhiskaalad korrutamiseks ja jagamiseks;
- A ja B – ruutude ja ruutjuurte jaoks;
- K – kuupjuurte ja kuubiga seotud arvutuste lihtsustamiseks;
- S ja T – siinus- ja tangentskaalad trigonomeetriliste arvutuste jaoks;
- L – logaritmiline skaal, mis näitab dekadilisi logaritme.
Lihtne näide – korrutamine ja jagamine
Korrutamiseks (näide 2,5 × 3,2):
- Seadista C-skaalal 1 (või märgitud ühik) vastavusse D-skaalal 2,5.
- Liiguta cursor või loe C-skaalalt 3,2 vastav koht; D-skaalal on nüüd vastav tulemus ≈ 8,00.
Praktiline märkus: slaidireegilt saad tavaliselt 2–4 tähte täpsust, sõltuvalt skaala pikkusest ja kasutaja oskusest. Kui on vaja rohkem täpsust, on levinud meetod tulemuse ümardamine või korrutamine/ülejäänud lugemine täiendavate abimeetoditega.
Tüübid ja eriversioonid
On palju erinevaid slaidireeglite stiile: lineaarsed (sirged) ja ringikujulised (circular). Lineaarsed on levinumad ja neid on tootnud palju firmasid. Ringikujulised ja silindrikujulised slaidireeglid annavad lühema mahutusega pikki skaalasid, mistõttu pakuvad suuremat täpsust ja vähem skaala lõputuse probleeme.
Mõned arvutuslükatid on valmistatud spetsiaalseks kasutamiseks, näiteks lennunduse (aviation) või rahanduse jaoks. Nendel mudelitel on lisaks tavalistele skaaladele ka spetsiaalsed skaalad ja tabelid just nende rakenduste jaoks (kütusekulu, õhukiirused, muundamised, finantstoonused jms).
Ajalugu lühidalt
William Oughtred ja teised teadlased arendasid 1600. aastatel välja kaasaegse slaidireegli idee. Lükandreegel põhineb John Napieri logaritmide alastel töödel ja Ameerika ning Euroopa leiutajate edasistel täiustustel. Enne elektrooniliste kalkulaatorite laialdast levikut olid arvutuslükatid teaduse ja tehnika valdkonnas igapäevased tööriistad. Slaidireeglite kasutamine jätkus 1950ndatel ja 1960ndatel aastatel isegi siis, kui järk-järgult võeti kasutusele digitaalarvutid; kuid 1974. aasta paiku muutis taskukalkulaator slaidireegli suurte mastaapide tõttu suuresti iganenuks ning enamik tootjaid lahkus sellest valdkonnast.
Täpsus, piirangud ja tugevused
Arvutuslükati tugevus on kiirus ja töökindlus ilma elektrita. Selle piirang on peamiselt täpsus (tavaliselt 3–4 olulist numbrit ühe skaala ulatuses) ning keerukamate operatsioonide (nt väga täpsed statistilised arvutused või suured numbrivahemikud) puhul on elektroonilised seadmed mugavamad. Slaidireeglite puhul tuleb tähele panna hüpoteetilisi vigu nagu skaala lugemise eksimus, temperatuuri ja niiskuse mõju (eriti puidust mudelitel) ning skaala suletuse (scale wrap) efekt ringikujulistel mudelitel.
Kasutamine ja hooldus
Slaidireeglit tuleks hoida tasasel pinnal ja kaitsta otsese päikese, niiskuse ning väga kõrgete või madalate temperatuuride eest — puidust ja liimitud mudelid võivad niiskusega deformeeruda. Indikaatoritäppe ei tohiks kummagi küljega liiga tugevalt pingutada. Puhastamiseks kasutatakse pehmet kuiva lappi; vajadusel väga vähest alkoholi plekieemalduseks. Õli ei ole tavaliselt soovitatav, kuna see võib koguda tolmu ja takistada libisemist — sobib kergelt kuiva silikoonipõhist pulbrit või spetsiaalne grafiitpulber, kui libisemine on probleemiks.
Kogumine ja hariduslik väärtus
Tänapäeval on slaidireeglid populaarsed kollektsionääride, ajaloohuviliste ja õpetajate seas. Paljud muuseumid eksponeerivad ajaloolisi näiteid, mis näitavad instrumentide arengut tehnoloogia ajaloos. Slaidireegli omandamisel on huvitav õppida selle kasutamist – see annab parema arusaamise logaritmide ja skaalaoperatsioonide olemusest ning arendab numbrimeelt.
Kui soovite, võin lisada samm-sammulise juhendi pildi- või diagrammiga (kui teil on konkreetne mudel või pilt olemas), või koostada lühikese õppematerjali algajale, kuidas slaidireeglit kasutada korduvate harjutuste kaudu.

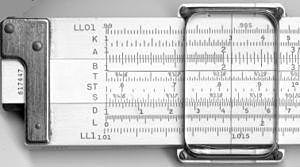
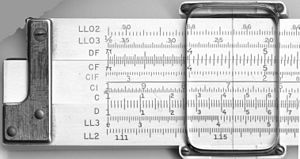
Tüüpiline kümnetolline õpilasarvuti (Pickett N902-T simplex trigonomeetriline arvutus)

Lükandjoonlaud, mis on paigutatud nii, et korrutatakse 2ga. Iga number D (alumine) skaala on kahekordne number C (keskmine) skaalal.
Põhimõisted
Kõige põhilisemal kujul kasutab arvutuslaud kaks logaritmilist skaalat, et võimaldada arvude kiiret korrutamist ja jagamist. Need tavalised operatsioonid võivad paberil tehes olla aeganõudvad ja veaohtlikud. Keerulisemad arvutuslaud võimaldavad muid arvutusi, näiteks ruutjuure, eksponentide, logaritmide ja trigonomeetriliste funktsioonide arvutamist.
Matemaatilised arvutused tehakse, viies libiseval keskribal oleva märgi vastavusse ühe fikseeritud ribaga. Seejärel saab jälgida teiste märkide suhtelist asendit. Märkidega joondatud numbrid annavad ligikaudse tulemuse, korrutise või muu arvutatud tulemuse väärtuse.
Kasutaja määrab kümnendmärgi asukoha tulemuses, tuginedes mentaalsele hinnangule. Ametlikumates arvutustes kasutatakse kümnendkohtade jälgimiseks teaduslikku märkimist. Liitmis- ja lahutamisetapid arvutustes tehakse tavaliselt mentaalselt või paberil, mitte arvutuslaual.
Enamikul joonlaudadel on kolm ühesuguse pikkusega lineaarset riba. Ribad on paralleelselt joondatud ja omavahel ühendatud, nii et keskmist riba saab pikisuunas kahe teise riba suhtes liigutada. Kaks välimist riba on fikseeritud, nii et nende suhteline asend ei muutu.
Mõnel liugreeglil ("dupleksmudelitel") on skaalad nii reegel kui ka liugriba mõlemal küljel, mõnel teisel on skaalad ühel pool välisriba ja mõlemal pool liugriba, mõnel teisel ainult ühel küljel ("simplex-reeglid"). Vertikaalse joondusjoonega libisevat kursorit kasutatakse vastavate punktide leidmiseks skaaladel, mis ei asu üksteise kõrval või dupleksmudelite puhul on joonlaua teisel poolel. Kursoriga saab salvestada ka vahepealse tulemuse mis tahes skaalal.

Kursor slaidireeglil
Arvutuste tegemiseks joonlaua kasutamine
Korrutamine
Logaritm teisendab korrutamise ja jagamise operatsioonid liitmiseks ja lahutamiseks vastavalt reeglitele log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} 











Operatsioonid võivad minna "skaalast välja"; näiteks ülaltoodud joonisel on näha, et arvutuslaud ei ole paigutanud ülemisel skaalal olevat 7-i ühegi arvu kohal alumisel skaalal, seega ei anna see vastust 2×7-le. Sellisel juhul võib kasutaja ülemist skaalat vasakule lükata, kuni selle paremal olev indeks on 2ga ühel joonel, mis tähendab, et ta korrutab 0,2ga, mitte 2ga, nagu alltoodud joonisel:
![]()
Siinkohal peab arvutuslaua kasutaja meeles pidama, et lõpliku vastuse korrigeerimiseks tuleb komakohta vastavalt korrigeerida. Me tahtsime leida 2×7, kuid selle asemel arvutasime 0,2×7=1,4. Seega ei ole tegelik vastus mitte 1,4, vaid 14. Slaidi ümberarvutamine ei ole ainus viis, kuidas käsitleda korrutamisi, mille tulemuseks oleks mitteskaalaline tulemus, näiteks 2×7; on ka teisi meetodeid:
- (1) Kasutage kahe kümnendi skaalasid A ja B.
- (2) Kasutage kokkuvolditud kaalusid. Selles näites seadke C vasakpoolne 1 vastas D 2. Viige kursor CF-i 7-le ja lugege tulemus DF-ist.
- (3) Kasutage CI ümberpööratud skaalat. Asetage 7 CI skaalal D skaala 2 kohale ja lugege tulemus D skaalalt alla 1 CI skaalal. Kuna 1 esineb CI-skaalal kahes kohas, on üks neist alati skaalal.
- (4) Kasutage nii CI invertskaalat kui ka C-skaalat. Joondage CI 2 ja D 1 kõrvuti ja lugege tulemus D-st C-skaala 7-st allapoole.
Meetodit 1 on lihtne mõista, kuid sellega kaasneb täpsuse vähenemine. Meetodi 3 eeliseks on see, et see hõlmab ainult kahte skaalat.
Osakond
Allpool olev joonis näitab arvutust 5,5/2. Ülemise skaala 2 on paigutatud alumise skaala 5,5 kohale. Ülemise skaala 1 asub kvooti 2,75 kohal. Jagamise tegemiseks on rohkem kui üks meetod, kuid siin esitatud meetodil on see eelis, et lõpptulemus ei saa olla skaalast väljas, sest on võimalik valida, kas kasutada 1 kummaski otsas.

Muud toimingud
Lisaks logaritmilistele skaaladele on mõnel arvutuslaual ka muid matemaatilisi funktsioone, mis on kodeeritud muudele abiskaaladele. Kõige populaarsemad olid trigonomeetrilised, tavaliselt siinus ja puutuja, tavaline logaritm (log10) (väärtuse logi võtmiseks korrutusskaalal), loomulik logaritm (ln) ja eksponentsiaalne (ex ) skaala. Mõned reeglid hõlmavad Pythagorase skaalat, et arvutada kolmnurkade külgi, ja skaalat, et arvutada ringe. Teistes on skaalad hüperboolsete funktsioonide arvutamiseks. Lineaarsetel reeglitel on skaalad ja nende tähistamine väga standardiseeritud, erinevused esinevad tavaliselt ainult selles, milliseid skaalasid ja millises järjekorras kasutatakse:
| A, B | kahe dekaadi logaritmiline skaala, mida kasutatakse arvude ruutjuurte ja ruutude leidmiseks |
| C, D | ühe kümnendi logaritmilised skaalad |
| K | kolmekümnendiklogaritmiline skaala, mida kasutatakse arvude kuubujuurte ja kuubikute leidmiseks |
| CF, DF | C- ja D-skaalade "volditud" versioonid, mis algavad π-st, mitte üksusest; need on mugavad kahel juhul. Esiteks, kui kasutaja arvab, et toode on 10 lähedal, kuid ei ole kindel, kas see on veidi väiksem või veidi suurem kui 10, välditakse volditud skaalade abil võimalust, et skaalast kõrvale kalduda. Teiseks, kuna algväärtus on π, mitte ruutjuur 10-st, siis lihtsustub paljundamine või jagamine π-ga (nagu on tavaline teaduse ja tehnika valemites). |
| CI, DI, DIF | "ümberpööratud" skaalad, mis kulgevad paremalt vasakule, mida kasutatakse 1/x sammude lihtsustamiseks. |
| S | mida kasutatakse D-skaala siinuste ja koosinuste leidmiseks. |
| T | mida kasutatakse puutuja ja kootangendi leidmiseks D- ja DI-skaalal. |
| ST, SRT | kasutatakse väikeste nurkade siinuste ja tangentside ning kraad-radiaanide teisendamiseks |
| L | lineaarne skaala, mida kasutatakse koos C- ja D-skaalaga 10 baasi logaritmide ja 10 punkte sisaldavate võimsuste leidmiseks. |
| LLn | log-log skaala, mida kasutatakse arvude logaritmide ja eksponentide leidmiseks |
| Ln | lineaarne skaala, mida kasutatakse koos C- ja D-skaaladega naturaal- (baas e) logaritmide ja e x {\displaystyle e^{x}} leidmiseks. |
| ||
| K&E 4081-3 arvutuslaua esi- ja tagaküljel olevad skaalad. |
Gilsoni 1931. aastal toodetud Binary Slide Rule (Binary Slide Rule) täitis liitmis- ja lahutamisfunktsiooni, mis piirdus murdudega.
Juured ja volitused
On olemas ühe kümnendi (C ja D), kahe kümnendi (A ja B) ja kolmekümnendi (K) skaalad. x 2 arvutamiseks {\displaystyle x^{2}} 
x y {\displaystyle x^{y}}

Trigonomeetria
S-, T- ja ST-skaalat kasutatakse trigonomeetriliste funktsioonide ja trigonomeetriliste funktsioonide korrutiste, kraadides väljendatud nurkade jaoks. Paljudel liugliteskaaladel S, T ja ST on märgitud kraadid ja minutid. Niinimetatud detsitrig mudelid kasutavad selle asemel kraadide kümnendmurdeid.
Logaritmid ja eksponentsiaalid
Alus-10 logaritmid ja eksponentsiaalid leitakse lineaarse L-skaala abil. Mõnedel liugliteskaaladel on Ln-skaala, mis on baasi e jaoks.
Ln skaala leiutas 11. klassi õpilane Stephen B. Cohen 1958. aastal. Esialgne eesmärk oli võimaldada kasutajal valida Ln skaalal eksponent x (vahemikus 0 kuni 2,3) ja lugeda ex C (või D) skaalal ja e–x CI (või DI) skaalal. Pickett, Inc. sai ainuõigused skaalale. Hiljem lõi leiutaja Ln-skaalal "märgid", et laiendada vahemikku üle 2,3 piiri, kuid Pickett ei lisanud neid märke kunagi ühelegi oma liugureale. []
Liitmine ja lahutamine
Liigutusreegleid ei kasutata tavaliselt liitmise ja lahutamise puhul, kuid seda on siiski võimalik teha kahe erineva tehnikaga.
Esimene meetod C ja D (või mõne võrreldava skaala) liitmise ja lahutamise teostamiseks nõuab probleemi teisendamist jagamise probleemiks. Liitmise puhul võrdub kahe muutuja korrutis pluss üks kord jagaja nende summaga:
x + y = ( x y + 1 ) y {\displaystyle x+y=\left({\frac {x}{y}}+1\right)y}
Lahutamise korral on kahe muutuja korrutis miinus üks kord jagaja võrdne nende vahega:
x - y = ( x y - 1 ) y {\displaystyle x-y=\left({\frac {x}{y}}-1\right)y}
See meetod on sarnane liitmis-/subtraktsioonimeetodiga, mida kasutatakse logaritmilise arvusüsteemiga kiirete elektrooniliste vooluahelate puhul spetsiaalsetes arvutirakendustes, nagu superarvuti Gravity Pipe (GRAPE) ja varjatud Markovi mudelid.
Teise meetodi puhul kasutatakse libisevat lineaarset L-skaalat, mis on saadaval mõnel mudelil. Liitmine ja lahutamine toimub kursori libistamisega vasakule (lahutamise puhul) või paremale (liitmise puhul) ja seejärel tulemuse lugemiseks libisemisega tagasi 0-le.
Füüsiline konstruktsioon
Standardsed lineaarsed reeglid
Liuguri pikkus on märgitud skaala nominaalpikkuses. Kõige tavalisemate "10-tolliste" mudelite skaalad on tegelikult 25 cm pikkused, kuna need on valmistatud meetriliste standardite järgi, kuigi mõned reeglid pakuvad veidi pikemaid skaalasid, et lihtsustada manipuleerimist, kui tulemus on ülevoolav. Taskureeglid on tavaliselt 5-tollised. Mõne meetri pikkuseid mudeleid müüdi selleks, et neid saaks õpetamise eesmärgil klassiruumidesse riputada. [1]
Tavaliselt tähistavad jaotused skaala kahe olulise numbri täpsusega ja kasutaja hindab kolmandat numbrit. Mõnel kõrgekvaliteedilisel arvutuslaual on suurendavad kursorid, mis muudavad märgistuse kergemini nähtavaks. Sellised kursorid võivad näitude täpsust kahekordistada, võimaldades 10-tollise joonlaua kasutamist sama hästi kui 20-tollise joonlaua puhul.
Välja on töötatud mitmesuguseid muid mugavusi. Trigonomeetrilised skaalad on mõnikord topeltmärgistatud, musta ja punase värviga, täiendavate nurkadega, nn Darmstadti stiilis. Kahepoolsetel liugreeglitel on sageli mõned skaalad tagaküljel dubleeritud. Suurema täpsuse saavutamiseks on skaalad sageli "jagatud".
Spetsiaalsed arvutuslükatid leiutati mitmesuguste inseneri-, äri- ja pangandusalade jaoks. Nendel olid sageli tavalised arvutused otseselt väljendatud spetsiaalsete skaalade kujul, näiteks laenude arvutused, optimaalsed ostukogused või konkreetsed insenerivõrrandid. Näiteks ettevõte Fisher Controls levitas kohandatud slaidireeglit, mis oli kohandatud tööstuslike vooluhulgaklappide sobiva suuruse valimiseks kasutatavate võrrandite lahendamiseks. []
Ringikujulised slaidireeglid
Ümmargusi liugureid on kahte põhitüüpi, üks kahe kursoriga (vasakul) ja teine liikuva ketta ja ühe kursoriga (paremal). Kahe kursoriga versioonid täidavad korrutamist ja jagamist, säilitades kursorite vahel kindla nurga, kui neid pööratakse ümber valimisnurga. Ühe kursoriga versioon töötab rohkem nagu tavaline arvutuslaud, kasutades skaalade asjakohast joondamist.
Ringikujulise joonlaua põhiline eelis seisneb selles, et tööriista pikim mõõde on vähendatud umbes 3 korda (st π võrra). Näiteks oleks 10 cm ringikujulise mõõtkava välisskaala maksimaalne täpsus võrdne 30 cm tavalise liuguri täpsusega. Ümmargused arvutuslükatid välistavad ka "skaalavälised" arvutused, sest skaalad on konstrueeritud nii, et need on "ümbritsetud"; neid ei pea kunagi ümber orienteerima, kui tulemused on 1,0 lähedal - arvutuslükatid on alati skaalal. Mittetsükliliste mittespiraalsete skaalade, nagu S, T ja LL, puhul on skaala pikkus siiski lühendatud, et teha ruumi lõppmarginaalide jaoks.
Ringikujulised liuglükandurid on mehaaniliselt vastupidavamad ja sujuvamalt liikuvad, kuid nende skaala joondamise täpsus sõltub keskse pöördepunkti tsentreerimisest; 0,1 mm kõrvalekaldumine pöördepunktist võib halvimal juhul põhjustada 0,2 mm joondamisvea. Pöördepunkt takistab siiski näo ja kursorite kriimustamist. Suurima täpsusega skaalad on paigutatud välisrõngastele. "Jagatud" skaalade asemel kasutatakse keerukamate operatsioonide, näiteks logaritmiliste skaalade puhul kõrgekvaliteediliste ringreeglite puhul spiraalseid skaalasid. Ühel kaheksa-tollisel kõrgklassi ringreeglil oli 50-tolline spiraalne log-log skaala.
Peamised puudused on ringikujulise joonlaua puhul raskused arvude leidmisel piki pöörlevat ketast ja piiratud arvu skaalasid. Veel üks ringikujulise arvutuslükati puudus on see, et vähem tähtsad skaalad on keskusele lähemal ja nende täpsus on väiksem. Enamik õpilasi õppis joonlaudade kasutamist lineaarsetel joonlaudadel ja ei leidnud põhjust nende vahetamiseks.
Üheks igapäevaselt kasutuses olevaks arvutuslükkainstrumendiks on E6B. See on ümmargune joonlaud, mis loodi esmakordselt 1930ndatel aastatel lennukipilootide jaoks, et aidata neil arvestust teha. Raamile trükitud skaalade abil aitab see ka mitmesuguste ülesannete täitmisel, näiteks aja, vahemaa, kiiruse ja temperatuuri väärtuste ümberarvestamisel, kompassivigade ja kütusekulu arvutamisel. Niinimetatud "palveratas" on endiselt saadaval lennupoodides ja seda kasutatakse endiselt laialdaselt. Ehkki GPS on vähendanud surnud punktlugemise kasutamist aeronavigatsioonis ja pihuarvutid on paljud selle funktsioonid üle võtnud, kasutatakse E6B-d endiselt laialdaselt esmase või varaseadmena ning enamik lennukoole nõuab, et nende õpilased valdaksid seda mingil määral.
1952. aastal tõi Šveitsi kellafirma Breitling välja piloodi käekella, millel oli integreeritud ringikujuline, lennukiarvutuste jaoks spetsialiseerunud joonlaud: Breitling Navitimer. Navitimer ringmõõdul, mida Breitling nimetas "navigatsioonikompuutriks", oli funktsioonid lennukiirus, tõusu/laskumise kiirus, lennuaeg, vahemaa ja kütusekulu, samuti funktsioonid kilomeetri-meremiili ja galloneliitri kütusekoguse ümberarvestamiseks.
Materjalid
Traditsiooniliselt valmistati joonlaudasid kõvast puidust, näiteks mahagonist või pukspuust, ning nende kursorid olid klaasist ja metallist. Vähemalt üks kõrge täpsusega instrument oli valmistatud terasest.
1895. aastal hakkas Jaapani firma Hemmi valmistama bambusest liuglustajaid, mille eeliseks oli mõõtmete stabiilsus, tugevus ja loomulik isevoolavus. Need bambusist liuglükandireeglid võeti Rootsis kasutusele 1933. aasta septembris [2] ja Saksamaal tõenäoliselt veidi varem. Kaalud olid valmistatud tselluloidist või plastist. Hilisemad joonlaudad olid valmistatud plastist või plastiga värvitud alumiiniumist. Hilisemad kursorid olid akrüül- või polükarbonaatidest, mis libisesid teflonlaagritel.
Kõikidele kõrgema klassi slaidireeglitele graveeriti numbrid ja skaalad ning seejärel täideti need värvi või muu vaiguga. Värvitud või trükitud joonlaudu peeti halvemaks, sest märgistus võis ära kuluda. Sellest hoolimata valmistas Pickett, tõenäoliselt Ameerika edukaim arvutuslükkainstrumendi ettevõte, kõik trükitud skaalad. Esmaklassilistel arvutusjuhenditel olid nutikad sulgurid, et arvutusjuhend ei kukuks kogemata laiali, ning kaitsed, mis kaitsevad skaalat ja kursorit lauaplaadil hõõrdumise eest. Graveeritud märkmete soovituslik puhastusmeetod on kergelt terasvillaga hõõruda. Värvitud joonlaudade puhul ja nõrganärviliste puhul kasutage lahjendatud kaubanduslikku aknapuhastusvedelikku ja pehmet lappi.

Pickett'i ringikujuline joonlaud kahe kursoriga. (4,25 tolli / 10,9 cm läbimõõduga) Tagaküljel on täiendav skaala ja üks kursor.

Lihtne ringikujuline arvutuslaud, mille on valmistanud Concise Co., Ltd., Tokyo, Jaapan, ja millel on ainult pöörd-, ruut- ja kuubiskaala. Tagaküljel on mugav loetelu 38 meetrilisest/keiserlikust ümberarvestustegurist.

Breitling Navitimer käekell koos ringikujulise liugregulaatoriga
Ajalugu
Lükandarv leiutati umbes 1620-1630, vahetult pärast seda, kui John Napier avaldas logaritmi mõiste. Edmund Gunter Oxfordist töötas välja ühe logaritmilise skaalaga arvutusvahendi, mida koos täiendavate mõõtmisvahenditega sai kasutada korrutamiseks ja jagamiseks. Selle skaala esimese kirjelduse avaldas 1624. aastal Pariisis inglise matemaatik Edmund Wingate (umbes 1593 - 1656) raamatus "L'usage de la reigle de proportion en l'arithmetique & geometrie". Raamat sisaldab kahekordset skaalat, mille ühel poolel on logaritmiline skaala ja teisel pool tabeli skaala. 1630. aastal leiutas William Oughtred Cambridge'ist ringikujulise arvutuslaua ja 1632. aastal kombineeris ta kaks Gunteri arvutuslauda, mida hoiti koos kätega, et luua seade, mis on äratuntavalt tänapäevane arvutuslaud. Nagu tema Cambridge'i kaasaegne Isaac Newton, õpetas ka Oughtred oma ideid eraviisiliselt oma õpilastele, kuid viivitas nende avaldamisega, ja nagu Newton, sattus ka ta oma kunagise õpilase Richard Delamaini ja Wingate'i varasemate väidete tõttu ägedasse vaidlusse prioriteedi üle. Oughtredi ideed avalikustati alles tema õpilase William Forsteri väljaannetes 1632. ja 1653. aastal.
1677. aastal lõi Henry Coggeshall puidu mõõtmiseks kahe jala pikkuse kokkuklapitava mõõdupuu, mida nimetati Coggeshalli mõõdupuuks. Tema konstruktsioon ja selle tööriista kasutusviisid andsid joonlaua otstarbekuse ka väljaspool matemaatilisi uuringuid.
1722. aastal võttis Warner kasutusele kahe- ja kolmekümnendskaala ning 1755. aastal lisas Everard ka ümberpööratud skaala; kõiki neid skaalasid sisaldavat joonlauda nimetatakse tavaliselt "mitmefaasiliseks" joonlauaks.
1815. aastal leiutas Peter Roget logaritmilogaritmiga libisemisarvu, mis sisaldas logaritmi logaritmi näitavat skaalat. See võimaldas kasutajal otseselt teha juurte ja eksponentidega seotud arvutusi. See oli eriti kasulik murdepowerite puhul.
Kaasaegne vorm
Kaasaegsema vormi lõi 1859. aastal Prantsuse suurtükiväe leitnant Amédée Mannheim, "kellel oli õnne, et tema reeglit valmistas riiklikult tuntud firma ja et Prantsuse suurtükivägi võttis selle kasutusele". Umbes sel ajal, kui inseneriteadusest sai tunnustatud kutsetegevus, hakkasid liugmehhanismid Euroopas laialdaselt kasutama. Ameerika Ühendriikides hakkasid need levima alles 1881. aastal, kui Edwin Thacher võttis seal kasutusele silindrilise joonlaua. Kahepoolse joonlaua leiutas William Cox 1891. aastal ja seda tootis New Yorgi Keuffel and Esser Co.
Astronoomiline töö nõudis ka peeneid arvutusi ja 19. sajandi Saksamaal kasutati ühes observatooriumis umbes 2 meetri pikkust terasest arvutuslükkainet. Selle külge oli kinnitatud mikroskoop, mis andis sellele täpsuse kuue kümnendikuni.
Teise maailmasõja ajal kasutasid pommimehed ja navigaatorid, kes vajasid kiireid arvutusi, sageli spetsiaalseid arvutuslauseid. Üks USA mereväe büroo konstrueeris tegelikult alumiiniumist korpuse ja plastikust kursoriga "šassii", millesse sai spetsiaalsete arvutuste tegemiseks asetada tselluloidkaarte (mõlemalt poolt trükitud). See protsess leiutati lennukite vahemaa, kütusekulu ja lennukõrguse arvutamiseks ning seejärel kohandati seda paljudeks muudeks eesmärkideks.
Kogu 1950ndate ja 1960ndate aastate jooksul oli joonlaud inseneri elukutse sümboliks (samamoodi nagu stetoskoop sümboliseerib arstide elukutset).[] Saksa raketiteadlane Wernher von Braun tõi kaks 1930. aastate Nestleri joonlauda kaasa, kui ta pärast Teist maailmasõda USAsse kolis, et töötada Ameerika kosmoseprogrammi kallal. Kogu oma elu jooksul ei kasutanud ta kunagi muid taskuarvutusseadmeid; slaidireeglid sobisid talle suurepäraselt raketi konstruktsiooni parameetrite ja muude arvude kiireks hindamiseks. Alumiiniumist Pickett'i marki slaidireeglid olid kaasas viiel Apollo kosmoselennul, sealhulgas Kuule, vastavalt Pickett'i N600 slaidireeglite kastide reklaamile [3].
Mõned inseneriteaduskonna üliõpilased ja insenerid kandsid vöökohvrites kümnetolliseid tõukeregulaatoreid ja isegi 1970. aastate keskpaigas oli see ülikoolilinnakutes tavaline nähtus. Samuti võisid üliõpilased hoida kodus või kontoris täpsustöödeks kümne- või kahekümnetollist joonlauda, kandes samal ajal kaasas viietollist taskuliblikat.
2004. aastal mõtlesid haridusteadlased David B. Sher ja Dean C. Nataro välja uut tüüpi arvutuslaua, mis põhineb prostaferoosil, mis on logaritmide eelne algoritm toodete kiireks arvutamiseks. Selle ehitamise vastu on aga pärast esialgset prototüüpi olnud vähe praktilist huvi. [4]
Langus
Arvutuslaua tähtsus hakkas vähenema, kui elektroonilised arvutid, mis olid 1950. aastatel uus, kuid väga napp ressurss, muutusid 1960. aastatel tehnikatöötajatele laialdaselt kättesaadavaks. Fortrani kasutuselevõtt 1957. aastal muutis arvutid praktiliseks tagasihoidlike matemaatiliste probleemide lahendamiseks. IBM tõi turule seeria taskukohasemaid arvuteid, IBM 650 (1954), IBM 1620 (1959), IBM 1130 (1965), mis olid suunatud teadus- ja inseneriturule. John Kemeny programmeerimiskeel BASIC (1964) tegi arvutite kasutamise õpilastele lihtsaks. DEC PDP-8 miniarvuti võeti kasutusele 1965. aastal.
Arvutid muutsid ka arvutamise olemust. Lükandreeglite puhul pöörati suurt tähelepanu algebra tööle, et saada väljendid võimalikult arvutatavale kujule. Arvutuste lihtsustamiseks lähendasid või jätsid väikeseid termineid lihtsalt välja, et arvutusi lihtsustada. Fortran võimaldas keerulisi valemeid õpikutest sisestada, ilma et oleks vaja neid ümber sõnastada. Numbriline integreerimine oli sageli lihtsam kui keerulistele probleemidele suletud kujul lahenduste leidmine. Noor insener, kes küsib arvutiaega, et lahendada probleem, mida oleks võinud lahendada mõne tõmbega joonlaual, muutus humoorikaks klišeeks. Paljudes arvutuskeskustes rippus seinale raamitud arvutuslükati joonlaud märkusega "Hädaolukorras purusta klaas".
Teine samm slaidireeglite asendamise suunas elektroonikaga oli elektrooniliste kalkulaatorite väljatöötamine teaduslikuks ja tehniliseks kasutamiseks. Esimesteks olid 1965. aastal kasutusele võetud Wang Laboratories LOCI-2, mis kasutas korrutamiseks ja jagamiseks logaritme, ja 1968. aastal kasutusele võetud Hewlett-Packard HP-9100. HP-9100-l olid lisaks eksponentidele ja logaritmidele ka trigonomeetrilised funktsioonid (sin, cos, tan). See kasutas CORDIC (coordinate rotation digital computer) algoritmi, mis võimaldab trigonomeetriliste funktsioonide arvutamiseks kasutada ainult nihke- ja liitmisoperatsioone. See meetod hõlbustas üha väiksemate teaduslike kalkulaatorite väljatöötamist.
Viimane nael arvutuslaua kirstus oli taskuformaadis teaduslike kalkulaatorite turuletoomine, millest esimene oli 1972. aastal Hewlett-Packardi HP-35. Selliseid kalkulaatoreid hakati nimetama "arvutuslaua" kalkulaatoriteks, kuna need võisid täita enamikku või kõiki arvutuslaua funktsioone. Mitmesaja dollari eest peeti isegi seda enamiku üliõpilaste jaoks kalliks. Kuigi ka professionaalsed arvutuslauaarvutid võisid olla üsna kallid, müüsid apteegipoed sageli lihtsaid plastmudeleid alla 20 USA dollari eest. Kuid 1975. aastaks võis põhilisi nelja funktsiooniga elektroonilisi kalkulaatoreid osta alla 50 dollari. Aastaks 1976 pakuti TI-30 teaduslikku kalkulaatorit alla 25 dollari. Pärast seda aega kuivas slaidireeglite turg kiiresti kokku, sest väikesed teaduslikud kalkulaatorid muutusid taskukohaseks.

William Oughtred (1575-1660), ringikujulise joonlaua leiutaja.

Insener, kes kasutab tõkkepuude abil. Taustal on mehaaniline kalkulaator.

TI-30
Eelised
- Lükandjoonlaud kipub "vale täpsuse" ja olulisuse eksitust leevendama. Tüüpiline täpsus, mis on liuglustaja kasutajale kättesaadav, on umbes kolme koha täpsus. See vastab hästi enamikule andmetele, mida saab sisestada tehnilistesse valemitesse. Kui kasutatakse kaasaegset taskuarvutit, võib täpsus olla näidatud seitsme või enama kümnendkohani, samas kui tegelikkuses ei saa tulemused kunagi olla täpsemad kui olemasolevad sisendandmed.
- Liuguri puhul on vaja pidevalt hinnata tulemuste suurusjärku. Liuguri 1,5 × 30 (mis võrdub 45) näitab sama tulemust kui 1 500 000 × 0,03 (mis võrdub 45 000). Insener peab pidevalt kindlaks tegema tulemuste mõistlikkuse, mis võib kaduma minna, kui numbrid sisestatakse hooletult arvutiprogrammi või kalkulaatorisse.
- Korrutamisel sama arvuga korrutamise või jagamise jada, saab vastuse sageli kindlaks teha pelgalt pilguga, ilma et sellega manipuleeritaks. See võib olla eriti kasulik protsentide arvutamisel, nt testitulemuste puhul, või hindade võrdlemisel, nt dollarites kilogrammi kohta. Mitmeid kiiruse-aja-kauguse arvutusi saab liuguri abil teha käed-vabalt ühe pilguga.
- Lükandarvuti ei sõltu elektrist.
- Liuguri on hõlpsasti reprodutseeritav tehnoloogia. Pädev käsitööline võib antud joonlaua näitel konstrueerida mittetööstuslikke protsesse kasutades algelistest materjalidest rohkem.
- Slaidireeglid on väga standardiseeritud, seega ei ole vaja midagi ümber õppida, kui vahetate mõne teise reegli vastu.
- Liuglahendused on mitmekülgsed ja neid saab kasutada olukordades ja keskkondades, kus inimese osavus võib olla piiratud (näiteks kaitsekindade kasutamise tõttu). Seevastu kalkulaatorit võib sellistes olukordades olla raske kasutada - liuguri puhul on ebatõenäoline, et tekib samasugune viga nagu kalkulaatori vale nupu valesti vajutamisel.
- Liugureeglid võivad olla valmistatud papist või paberist. Paljud kartongist valmistatud tasuta graafikud või spetsiaalsed arvutusseadmed on tegelikult spetsiaalsed lineaarsed või ringikujulised liugureeglid.
Üks eelis, mis on arvutuslaua ja elektroonilise kalkulaatori kasutamisel, on see, et olulist arvutust saab kontrollida, tehes seda mõlemaga; kuna need kaks instrumenti on nii erinevad, on vähe võimalusi teha sama viga kaks korda.
Puudused
- Vead võivad tuleneda mehaanilisest ebatäpsusest.
- Arvutused, mille puhul kasutatakse arvutuslükkainet, on piiratud täpsusega, sest nende analoogsisendid ja -väljundid on piiratud. Seevastu diskreetsete numbriliste sisendite ja elektrooniliste ujukomaoperatsioonide tõttu on isegi tagasihoidlike kaasaegsete kalkulaatorite väljundresolutsioon vähemalt kuus olulist numbrit.
Seotud leheküljed
Küsimused ja vastused
K: Mis on liugur?
V: Lükandarvuti on mehaaniline analoogarvuti, mida kasutatakse peamiselt korrutamiseks ja jagamiseks, samuti teaduslikeks funktsioonideks, näiteks juurte, logaritmide ja trigonomeetria jaoks.
K: Millised on eri tüüpi arvutuslükke?
V: Lükandreeglid võivad olla lineaarsed või ümmargused ja neil on standardiseeritud tähised või skaalad, mida kasutatakse matemaatiliste arvutuste tegemiseks. Mõned erikasutuseks mõeldud arvutuslaudad on valmistatud lennunduse või rahanduse jaoks, millel on nende rakenduste jaoks spetsiaalsed skaalad.
K: Kes leiutas arvutuslükkainstrumendi?
V: Tõkkejoonlaua leiutas William Oughtred John Napieri logaritmidega seotud tööde põhjal.
K: Millal töötati välja elektroonilised kalkulaatorid?
V: Elektroonilised kalkulaatorid töötati välja enne 1970. aastaid, kuid umbes 1974. aasta paiku muutis taskukalkulaator arvutuslaua suures osas iganenuks.
K: Mida kasutasid inimesed enne elektrooniliste kalkulaatorite väljatöötamist kõige sagedamini teaduses ja tehnikas?
V: Enne elektrooniliste kalkulaatorite väljatöötamist kasutasid inimesed teaduse ja tehnika valdkonnas kõige sagedamini arvutuslauda.
K: Kui kaua inimesed jätkasid arvutuslaua kasutamist pärast digitaalarvutite kasutuselevõttu?
V: Inimesed jätkasid joonlaua kasutamist 1950. ja 1960. aastatel, isegi kui järk-järgult võeti kasutusele digitaalarvutid.
Otsige