Korrutamine: definitsioon, omadused ja näited
Korrutamine: selge definitsioon, omadused (kommutatiivsus, skaleerimine), visuaalsed näited ja praktilised selgitused algajatele ja edasijõudnutele.
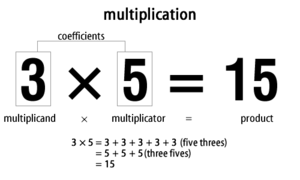
Korrutamine on aritmeetiline operatsioon kahe arvu korrutise leidmiseks. Lihtsaimas tähenduses saab korrutamist vaadata kui korduvat liitmist: a × b tähendab arvu a liitmist enda endaga b korda (kui b on loomulik arv). Korrutamist tähistatakse erinevalt: tavaliselt märgiga ×, vahel ka punktiga (·) või tärniga (*).
Määratlus ja tähendus
Loogilisemalt kui ainult korduv liitmine, mõistetakse korrutamist ka suuruste skaleerimisena. Näiteks kui üks külg ristkülikul on pikkusega 3 ja teine 5, siis nende korrutis annab ristküliku pindala (3 × 5 = 15). Loomulike arvude korral vastab see ruutude arvu kahemõõtmelises võrgus.
Näide: 3 × 5 = 15 (loetakse "kolm korda viis võrdub viieteistkümnega").
Põhiomadused
- Kommutatiivsus: korrutamise järjekord ei mõjuta tulemust: a × b = b × a. See kehtib näiteks täisarvude, ratsionaalarvude, kõigi reaalarvude ja kompleksarvude puhul.
- Assotsiatiivsus: (a × b) × c = a × (b × c) — järjestuse grupeerimine ei muuda tulemust.
- Distributiivsus: a × (b + c) = a × b + a × c — korrutamine jaguneb liitmise üle.
- Neutraalarv: 1 on korrutamise neutraalne element, sest a × 1 = a.
- Nulli omadus: iga arvu korrutis nulliga on null: a × 0 = 0.
Matemaatikud kutsuvad korrutatavaid tavaliselt tegureks või korrutisanditeks (või eesti keeles ka korrutajad); tulemust nimetatakse korrutiseks või produktiks.
Erijuhud ja märgiga arvud
- Kui üks teguritest on negatiivne ja teine positiivne, on korrutis negatiivne: (-3) × 5 = -15.
- Kui mõlemad tegurid on negatiivsed, on korrutis positiivne: (-3) × (-5) = 15.
- Nulliga korrutamisel saadakse alati 0: 0 × a = 0.
Korrutamine erinevate arvitüüpide vahel
- Murud: (a/b) × (c/d) = (a × c) / (b × d).
- Detsembid: korrutamisel korrutada mõlemad väärtused ja vajadusel nihutada koma. Korrutamine kümnendkohtadega on mugavam teisendada alguses murdudeks või kasutada standardset arvutustehnikat.
- Kompleksarvud: korrutamine on ka siin defineeritud ja kommutatiivne; (a + bi)(c + di) = (ac − bd) + (ad + bc)i.
- Vektorite ja maatriksite korrutamine ei ole üldjuhul kommutatiivne: A·B ei pruugi võrduda B·A ja mõnikord on korrutis teostamatu, kui mõõtmed ei sobi.
- Kvaternionid on näide algebraabstraktsetest elementidest, mille korrutamine ei ole kommutatiivne.
Distributiivsuse ja hulgateoreetiline tõlgendus
Korrutamise määratlus korduva liitmisena annab võimaluse laiendada mõistet ka kardinaalsete arvude puhul ja hulgateoreetiliselt mõelda produktist kui kaardistusest või paari koostamisest. Distributiivsus aitab ühendada korrutamist ja liitmist algebra tasandil.
Tõlgendused ja rakendused
- Pindala ja geomeetria: ristküliku pindala on külgede pikkuste korrutis.
- Skaleerimine: korrutamine skaleerib suurusi (x kordamine y-ga tähendab x skaleerimist faktoriga y).
- Arvutusalgoritmid: tavapärane kaua-korrutamise ehk "long multiplication" algoritm, kiirendatud meetodid (nt Karatsuba), ning tänapäevased FFT-põhised algoritmid suurtel täisarvudel.
- Igapäevased näited: hindade arvutamine, pindalade leidmine, mõõtmised, tangendi skaleerimine graafikus jpm.
Praktilised näited
- 3 × 5 = 15 — kolm korda viis on viisteist.
- 4 × (2 + 3) = 4 × 2 + 4 × 3 = 8 + 12 = 20 (distributiivsus).
- (1/2) × (3/4) = 3/8 (murdude korrutamine).
- (-2) × (-7) = 14 (kaks negatiivset tegurit annavad positiivse tulemuse).
Õpivinkid
- Õpi korrutustabelid 1–10 kiiresti — need on praktilised ja kiirendavad aritmeetikat.
- Kasuta visuaalseid kujutisi (nt ruudustik, ristkülik) mõistmaks üldist õiget tähendust korrutamisel.
- Praktiseeri nii positiivsete, negatiivsete kui murdarvude korrutamist, et mõista mudeleid ja mustreid.
Kui soovite, võin lisada selgeid samm-sammulisi juhendeid pikaajalise korrutamise kohta, interaktiivseid näiteid või ülesandeid harjutamiseks.
Korrutamise vastand on jagamine.
Korrutustabel
Korrutamise õpetamisel nõuavad õpetajad tavaliselt, et õpilased õpiksid meelde 9 esimese numbri tabeli.
| Tabel 6-st | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Korrutustabel | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Seotud leheküljed
- Lisandumine
- Ruutnumber
- Subtraktsioon
Küsimused ja vastused
K: Mis on korrutamine?
V: Korrutamine on matemaatikas kahe arvu korrutise leidmise aritmeetiline operatsioon. Seda kujutatakse sageli selliste sümbolitega nagu × ja ⋅.
K: Kuidas nimetatakse kahte arvu, mida korrutatakse?
V: Kahte korrutatavat arvu nimetatakse "koefitsientideks" või "korrutisandiks" ja "korrutisandiks" eraldi.
K: Kas korrutamine on kommutatiivne?
V: Jah, arvude korrutamist nimetatakse kommutatiivseks - kui arvude järjestus ei mõjuta korrutise väärtust. See kehtib täisarvude, ratsionaalarvude, reaalarvude ja kompleksarvude puhul. See ei kehti aga kvaternioonide, vektorite või maatriksite kohta.
Küsimus: Kuidas saab tõlgendada kardinaalsete arvude korrutamist?
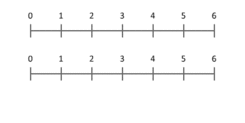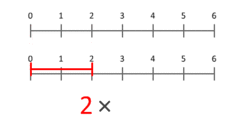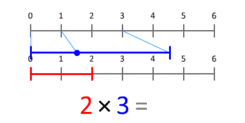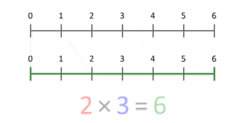
V: Kardinaalarvude korrutamist saame tõlgendada kui suuruste skaleerimist - kui üks arv (korrutisandja) skaleeritakse nii, et 1. positsioonile paigutatud punkt satub teatud punkti (korrutisandja).
Küsimus: Kuidas kujutatakse kolm korda viiega korrutatuna?
V: Kolm korrutatud viiega võib kirjutada kui 3 × 5 = 15 või rääkida kui "kolm korda viis võrdub viieteistkümnega".
K: Mis on korrutamise vastand?
V: Korrutamise vastand on jagamine.
Otsige