Shape of the universe
Universumi kuju ei saa arutada igapäevaste terminitega, sest kõik terminid peavad olema Einsteini relatiivsusteooria terminid. Universumi geomeetria ei ole seega meie igapäevaelu tavaline eukleidiline geomeetria.
Vastavalt relatiivsusteooria eriteooriale on võimatu öelda, kas kaks erinevat sündmust toimuvad samal ajal, kui need sündmused on ruumiliselt eraldatud. Rääkida "universumi kujust (mingis ajahetkel)" on erirelatiivsusteooria seisukohalt naiivne. Samaaegsuse relatiivsuse tõttu ei saa me rääkida erinevatest punktidest ruumis, mis asuvad "ühes ja samas ajahetkes", ega seega ka "universumi kujust ühes ajahetkes".
Astrofüüsikud küsivad, kas konkreetne universumi mudel on kooskõlas sellega, mida teame universumi vaatluste ja mõõtmiste põhjal. Kui vaadeldav universum on väiksem kui kogu universum (mõnes mudelis on see mitu suurusjärku väiksem või isegi lõpmatult väike), siis piirdub vaatlus vaid ühe osaga tervikust.
Universumi kuju käsitlemise võib jagada kaheks:
- lokaalne geomeetria, mis on seotud eelkõige universumi kumerusega, eriti vaadeldavas universumis, ja
- globaalne geomeetria, mis on seotud universumi kui terviku topoloogiaga, mille mõõtmine ei pruugi olla võimalik.
Vaateldav universum on alus mis tahes universumi mudeli testimiseks. See on sfääriline ruumala (pall), mille keskmes on vaatleja, sõltumata universumi kui terviku kujust. Igas kohas universumis on oma vaadeldav universum, mis võib kattuda või mitte kattuda Maale keskendunud universumiga.
Hiljutised mõõtmised on pannud NASAd väitma: "Me teame nüüd, et universum on lame, ainult 0,4% veamarginaaliga". Ühe mudeli, FLRW-mudeli raames on praegu kõige populaarsem universumi kuju, mis sobib vaatlusandmetega, lõpmatult lame mudel. On ka teisi mudeleid, mis sobivad andmetega.
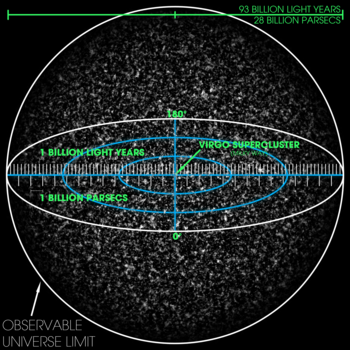
93 miljardi valgusaasta ehk 28 miljardi parseki pikkuse kolmemõõtmelise vaadeldava universumi visualiseerimine. Skaala on selline, et peened terad kujutavad suure hulga superklastrite kogumeid. Virgo superhulga - Linnutee koda - on tähistatud keskel, kuid see on liiga väike, et seda pildil näha.
Küsimused ja vastused
K: Milline on universumi kuju praeguste vaatluste kohaselt?
V: Hiljutiste mõõtmiste kohaselt on NASA teatanud, et universum on lame, kusjuures veamäär on vaid 0,4%.
K: Kuidas mõjutab eriline relatiivsusteooria meie arusaamist universumi kujust?
V: Samaaegsuse relatiivsusteooria tõttu on võimatu öelda, kas kaks erinevat sündmust toimuvad samal ajal, kui need sündmused on ruumis lahutatud. See tähendab, et me ei saa rääkida erinevatest punktidest ruumis, mis asuvad "samal ajahetkel", ega seega ka "universumi kujust mingil ajahetkel".
Küsimus: Millist geomeetriat kasutavad astrofüüsikud, kui nad räägivad universumi kujust?
V: Astrofüüsikud kasutavad Einsteini relatiivsusteooriat, kui nad arutavad ja katsetavad mudeleid, millega kirjeldatakse ja ennustatakse universumi aspekte. Nad kaaluvad ka kohalikku geomeetriat, mis on seotud eelkõige kumerusega, ja globaalset geomeetriat, mis on seotud topoloogiaga.
K: Kas iga koht Universumis on osa vaadeldavast universumist?
V: Jah, igal paigal Universumis on oma vaadeldav universum, mis võib kattuda või mitte kattuda Maale keskendunud universumiga.
K: Mida tähendab "lame", kui viidatakse Universumi aspekte kirjeldavale/ennustavale mudelile?
V: Ühes mudelis, mida nimetatakse FLRW (Friedmann-Lemaître-Robertson-Walker), viitab "lame" lõpmatult lamedale mudelile, mis sobib kõige paremini vaatlusandmetega. See tähendab, et ruum näib olevat ühtlane, ükskõik kuhu te vaatate, ja selles konkreetses mudelis ei ole mingeid kõverusi ega kõverusi.
Küsimus: Kas lisaks FLRW lõpmatult lamedale mudelile on olemas ka teisi mudeleid, mis sobivad vaatlusandmetega?
V: Jah, lisaks FLRW lõpmatult lamedale mudelile on ka teisi mudeleid, mis sobivad vaatlusandmetega.
