Mõõtmed (dimensioonid) — definitsioon, 3D, 4D, matemaatika ja füüsika
Mis on mõõtmed?
Mõõtmed kirjeldavad, kuidas me näeme, mõõdame ja kogeme maailma ning kuidas me määratleme objektide asukohti ja omadusi. Mõiste hõlmab nii ruumilisi suundi (näiteks üles–alla, paremalt–vasakule, ette–taha) kui ka teisi mõõdetavaid tunnuseid (näiteks aeg, temperatuur, mass). Mõõtme mõiste täpne tähendus sõltub kontekstist — igapäevaelus, matemaatikas või füüsikas — ning üheainsa, kõikide kasutusjuhtude peal kehtiva definitsiooni leidmine ei pruugi olla võimalik.
Mõõtmete tüübid ja kasutus
- Positsioonimõõtmed: kirjeldavad objekti või sündmuse asukohta. Näiteks kolmemõõtmelises ruumis annavad pikkus, laius ja kõrgus iga punkti positsiooni.
- Ajamõõde: aeg kasutatakse sageli neljanda mõõtmena, et määrata sündmuse aega ruumis toimunu suhtes.
- Kvantitatiivsed mõõtmed: sellised suurused nagu temperatuur või mass ei ole ruumilised suunad, kuid neid samuti nimetatakse mõõtmeteks, sest need kirjeldavad objekti omadusi ja on mõõdetavad.
- Abstraktsed mõõtmed: matemaatikas ja insenerteaduses võidakse käsitleda suvalist hulka mõõtmeid (n‑mõõtmeline ruum), kus iga dimensioon on üks sõltumatu koordinaat.
Vektorruum ja dimensioon
Vektorruumis mõistetakse dimensiooni kui sõltumatute suunavektorite (baasi) arvu, mille abil saab esitada kõiki ruumi vektoreid. Lihtsamalt öeldes on dimensioon võrdne vajalike koordinaatide arvuga punkti täpseks määratlemiseks selles ruumis. Näiteks tavalises elus tajutavas ruumis on kolm sõltumatut suunda — pikkus, laius ja sügavus — seega dimensioon on kolm.
2D, 3D ja n‑mõõtmeline ruum
Kahe- ja kolmemõõtmelised ruumid on kõige sagedasemad igapäevakeskkonnas:
- 2D (kahemõõtmeline) — pind, millel on kaks koordinaati (näiteks x ja y). Näiteks joonis, kaart või ekraanipilt on peaaegu kahemõõtmeline.
- 3D (kolmemõõtmeline) — ruum, kus on kolm sõltumatut koordinaati (x, y, z); seda tajume meie igapäevases füüsilises maailmas.
- n‑mõõtmeline ruum — matemaatikas ja andmeteaduses kasutatakse ruume, kus mõõtmete arv võib olla suvaliselt suur. Näiteks andmekogumite iga tunnus võib olla üks mõõde.
Neljas mõõde ja aeg (4D)
Mõnikord lisatakse kolmele ruumilisele mõõtmele ka aeg, et kirjeldada sündmuse positsiooni nii ruumis kui ka ajas. See lähenemine on eriti tähtis füüsikas ja relativistlikus kirjelduses, kus ruum ja aeg moodustavad ühtse neljamõõtmelise "ruumi‑aja" struktuuri. Aja kaasamine võimaldab täpselt kirjeldada, millal ja kus mingi sündmus aset leidis.
Mõõtmete roll matemaatikas ja füüsikas
Matemaatikas on dimensioon abstraktne omadus, mida hinnatakse erinevate kategooriate kaudu: vektorruumi dimensioon, topoloogiline dimensioon ja fraktaalne (murruline) dimensioon. Näiteks matemaatikas uuritakse, kuidas dimensioon mõjutab geomeetria ja analüüsi omadusi. Füüsikas mõõtmed määravad, kuidas objektid liiguvad, kuidas jõud toimivad ja kuidas ruum‑aeg on struktureeritud.
Mõned täiendavad mõisted
- Vabadusastmed: sageli kasutatakse mõõtmeid vabadusastmete kirjeldamiseks — kui palju sõltumatuid suundu on objektil liikumiseks.
- Topoloogiline dimensioon: kirjeldab objekti "pinnalist" omadust (näiteks joonel on topoloogiline dimensioon 1, pinnal 2).
- Fraktaalne dimensioon: mõnel kujul (näiteks looduse fraktalsetel struktuuridel) ei ole mõõtme väärtus täisarvuline; seda kasutatakse keerukuse ja korduvuse kirjeldamiseks.
Kokkuvõte
Mõõtmed annavad raamistikku, mille abil kirjeldame maailmas olevaid paiku, liikumisi ja omadusi. Sõltuvalt kontekstist võivad need olla ruumilised koordinaadid, aeg, füüsikalised suurused või abstraktsed matemaatilised dimensioonid. Mõistmine, kuidas dimensioonid töötavad, aitab nii igapäevastes tegevustes (nt mõõtmised, modelleerimine) kui ka sügavamates teaduslikes selgitustes (nt relativistlik füüsika, matemaatika) paremini orienteeruda keerukates süsteemides.
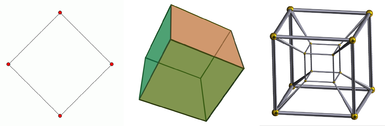
Vasakult paremale: ruut, kuup ja tesserakt. Ruut on 2-mõõtmeline objekt, kuup on 3-mõõtmeline objekt ja tesserakt on 4-mõõtmeline objekt. 1-mõõtmeline objekt on lihtsalt joon. Kuubiku projektsioon on antud, kuna seda vaadeldakse kahemõõtmelisel ekraanil. Sama kehtib ka tesserakti kohta, mida lisaks saab näidata ainult projektsioonina ka kolmemõõtmelises ruumis.
Nelja esimese ruumilise mõõtme diagramm.
Muud mõõtmed
Kaasaegses teaduses kasutavad inimesed teisi mõõtmeid. Mõõtmeid nagu temperatuur ja kaal saab kasutada selleks, et näidata millegi asukohta vähem lihtsates ruumides. Teadlane uurib neid dimensioone mõõtmeanalüüsiga.
Ka matemaatikud kasutavad mõõtmeid. Matemaatikas on mõõtmed üldisemad. Matemaatika dimensioonid ei pruugi mõõta maailma asju. Matemaatika mõõtmetega aritmeetika tegemise reeglid võivad erineda tavalistest aritmeetika reeglitest.
Mõõtmed ja vektorid
Vektoreid kasutatakse vahemaade ja suundade näitamiseks. Vektoreid kasutatakse sageli inseneriteadustes ja loodusteadustes ning mõnikord ka matemaatikas.
Vektor on numbrite loend. Iga mõõtme kohta on üks number. Vektorite jaoks on olemas aritmeetilised reeglid.
Näiteks kui Jane tahab teada Sally asukohta, võib Sally anda Jane'ile vektori, mis näitab tema asukohta. Kui Jane ja Sally on maailmas, siis on kolm mõõdet. Seetõttu annab Sally Jane'ile tema asukoha näitamiseks kolme arvu loendi. Kolm numbrit vektoris, mille Sally annab Jane'ile, võivad olla järgmised:
- Sally kaugus Jane'ist põhja pool
- Sally kaugus Jane'ist ida pool
- Sally kõrgus Jane'i kohal
Küsimused ja vastused
K: Mis on dimensioon?
A: Mõõde on viis, kuidas mõõta, näha ja kogeda maailma, kasutades selliseid mõisteid nagu üles ja alla, paremalt vasakule, tagant ette, kuum ja külm, kui raske ja kui pikk. Seda võib määratleda ka kui vabadusastmeid või seda, kuidas objekt saab konkreetses ruumis liikuda.
K: Kuidas defineerivad matemaatikud eukleidilist ruumi?
V: Matemaatikud määratlevad eukleidilist ruumi kolme mõõtmega, mida tavaliselt nimetatakse pikkuseks, laiuseks ja sügavuseks.
K: Kui palju on vektoreid vektorruumis?
V: Vektorite arv vektorruumis on võrdne selle alusgrupi kardinaalsusega (ehk vektorite arvuga).
K: Mitu dimensiooni kasutatakse positsiooni mõõtmiseks?
V: Asukoha mõõtmiseks kasutatakse kolme mõõdet (pikkus, laius ja kõrgus). Mõnel juhul võib kasutada ka neljandat (4D) mõõdet - aega -, et näidata sündmuse asukohta ajas ja ruumis.
K: Mida tähendab dim(V)?
V: Dim(V) viitab V dimensioonile, mis on võrdne tema alusgrupi kardinaalsusega (ehk vektorite arvuga) või võrdne tema sirgete suundade arvuga.
K: Kas on olemas üks definitsioon, mis rahuldab kõiki mõõtmetega seotud mõisteid?
V: Ei, ei ole olemas ühte definitsiooni, mis rahuldaks kõiki mõõtmetega seotud mõisteid.
