Histogramm
Histogramm on statistika mõiste. See on graafiline kujutis, mis annab meile teavet asjaomaste valimite jaotuse kohta. Need on tavaliselt paljude kategooriatega tabelist tehtud joonis. Tabelis on kirjas, mitu valimit on igas kategoorias.
Sõna histogramm tuleneb kreeka keeles histos ja gramma sõnadest. Histos tähendab võrku või masti. Gramma tähendab joonistust, salvestust või kirjutamist. Seega on histogramm millegi kohta etümoloogiliselt võttes selle millegi veebi joonistus.
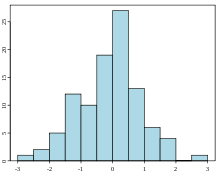
Näide 100 normaalselt jaotunud juhusliku väärtuse histogrammi kohta
Sarnased ideed
Histogramm on üks seitsmest kvaliteedikontrolli põhivahenditest, mille hulka kuuluvad ka Paretodiagramm, kontroll-leht, kontrollkaart, põhjus-tagajärg diagramm, vooskeem ja hajuvusdiagramm.
Histogrammi üldistus on kerneli silumise tehnika. See konstrueerib esitatud andmete põhjal sileda tõenäosustiheduse funktsiooni.
Küsimused ja vastused
K: Mis on histogramm?
V: Histogramm on graafiline kujutis, mis annab meile teavet asjaomaste valimite jaotuse kohta.
K: Mis on histogrammi eesmärk?
V: Histogrammi eesmärk on näidata asjaomaste valimite jaotust.
K: Mida tähendab sõna histogramm?
V: Sõna histogramm tuleneb kreeka keeles sõnadest histos ja gramma. Histos tähendab võrku või masti. Gramma tähendab joonistust, kirja või kirja.
K: Mida tähendab mõiste "histos" kreeka keeles?
V: Mõiste "histos" tähendab kreeka keeles võrku või masti.
K: Mida tähendab kreeka keeles mõiste "gramma"?
V: Mõiste "gramma" tähendab kreeka keeles joonistust, kirja või kirja.
K: Mis on histogrammi ühine tunnus?
V: Histogrammi ühiseks tunnuseks on paljude kategooriatega tabelist tehtud pilt.
K: Millist teavet annab histogrammi tabel?
V: Histogrammi tabel annab teavet selle kohta, mitu proovi on igas kategoorias.
