Tihedusfunktsioon

Tõenäosustustihedusfunktsioon on funktsioon, mida saab defineerida mis tahes pideva tõenäosusjaotuse jaoks. Tõenäosuse tihedusfunktsiooni integraal intervallis [ a , b ] {\displaystyle [a,b]} $[a,b]$ annab tõenäosuse, et antud juhuslik muutuja antud tihedusega sisaldub antud intervallis.

Tõenäosustustiheduse funktsioon on vajalik selleks, et töötada pidevate jaotustega. Nopaga viskamine annab arvud 1 kuni 6, tõenäosusega 1 6 {\displaystyle {\tfrac {1}{6}}} ${\tfrac {1}{6}}$ , kuid see ei ole pidev funktsioon, sest võimalikud on ainult numbrid 1 kuni 6. Seevastu kahel inimesel ei ole sama pikkust ega kaalu. Kasutades tõenäosustihedusfunktsiooni, on võimalik määrata tõenäosus, et inimesed on 180 sentimeetri ja 181 sentimeetri või 80 kilogrammi ja 81 kilogrammi vahel, kuigi nende kahe piiri vahel on lõpmatult palju väärtusi.

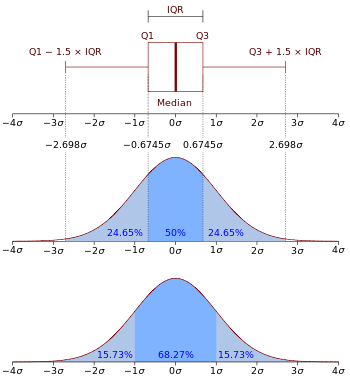
N (0, σ2) normaaljaotuse boksdiagramm ja tõenäosustiheduse funktsioon.

Küsimused ja vastused

K: Mis on tõenäosustiheduse funktsioon?

V: Tõenäosustustiheduse funktsioon on funktsioon, mis iseloomustab mis tahes pidevat tõenäosusjaotust.

K: Kuidas kirjutatakse juhusliku muutuja X tõenäosustihedusfunktsioon?

V: X-i tõenäosustihedusfunktsiooni kirjutatakse mõnikord kui f_X(x).

K: Mida kujutab endast tõenäosustihedusfunktsiooni integraal?

V: Tõenäosuse tihedusfunktsiooni integraal kujutab tõenäosust, et antud juhuslik muutuja antud tihedusega sisaldub etteantud intervallis.

K: Kas tõenäosustihedusfunktsioon on kogu oma alal alati mittenegatiivne?

V: Jah, määratluse kohaselt on tõenäosustihedusfunktsioon kogu oma alal mittenegatiivne.

K: Kas integreerimine üle intervalli annab summa 1?

V: Jah, integreerimine üle intervalli on summaarne 1.

K: Millist tüüpi jaotust iseloomustab tõenäosustihedusfunktsioon?

V: Tõenäosustustiheduse funktsioon iseloomustab mis tahes pidevat tõenäosusjaotust.