Tõenäosus
Tõenäosus on osa rakendusmatemaatikast. See on seotud tõenäosusega, mille puhul uuritakse asju, mis võivad juhtuda või mitte juhtuda.
Näiteks saab tõenäosuse abil näidata, et kui viskate mündi õhku ja lasete tal maanduda, siis pooltel juhtudel maandub see ühe küljega ülespoole ja pooltel juhtudel teise küljega ülespoole. Paljudel müntidel on ühel küljel mõne kuulsa inimese näo kujutis ja teisel küljel midagi muud. Tihtipeale kutsuvad inimesed näoga külge "pähe" ja teist külge "sabaks".
Sündmuse tõenäosus (p) jääb alati nulli (võimatu) ja ühe (kindel) vahele.
Kui me viskame täringut (mitmuses: dice), siis tõenäosus, et see langeb 1 peale, on 1/6 (see on tingitud sellest, et täringul on 6 numbrit). Samuti on tõenäosus, et see langeb 2-le, 1/6. See tuleneb sellest, et see võib langeda 1, 2, 3, 4, 5 või 6 peale. Tõenäosus, et mis tahes number vahemikus 1-6 langeb, on 1. Iga kord, kui me täringut veeretame, langeb see alati numbrile vahemikus 1-6.
Tõenäosust saab välja arvutada matemaatika abil. Näiteks kui visata kuus täringut, ei ole tõenäosus, et sa saad numbri, mis on suurem kui kümme, ilmselge, kuid seda saab välja arvutada matemaatika ja teaduse abil.
Üks huvitavamaid asju juhuse kohta on see, et selleks, et välja arvutada tõenäosus, et kaks asja mõlemad juhtuvad, korrutad nende kaks tõenäosust kokku. Oletame näiteks, et tahate teada tõenäosust, et kahe täringuga visates saate teatud kombinatsiooni (see võib olla kaks 6 või 3 ja seejärel 5, lihtsalt kaks mis tahes kombinatsiooni). Võimalus saada 3 on üks kuuest (⅙) ja võimalus saada 5 on samuti üks kuuest, seega tõenäosus saada 3 ja seejärel 5 on ⅙×⅙=⅟36. Kui seda arvu väljendada kusagil 0 ja 1 vahel, siis on see 0,027...7, mis on üsna väike. Võimalus saada 3, siis 5 ja siis 2 oleks ⅙×⅙×⅙×⅙=⅟216 ehk 0,00463, mis on palju väiksem tõenäosus.
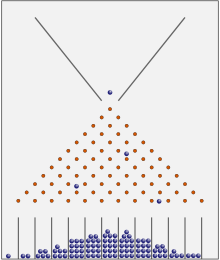
Oamasinas või Galtoni kastis jõuab enamik palle keskuse lähedale. Pikemas perspektiivis näitavad nad normaaljaotust.
Tõenäosuse ideed
Sellised inimesed nagu Jacob Bernoulli, Pierre-Simon Laplace või Christiaan Huygens kasutasid sõna tõenäosus, nagu eespool kirjeldatud. Teised inimesed mõtlesid sageduste kohta; nende tõenäosuse mõistet nimetatakse tavaliselt sagedustõenäosuseks.
Seotud leheküljed
- Matemaatika teemade loetelu
- Tõenäosusteooria
Küsimused ja vastused
K: Mis on tõenäosus?
V: Tõenäosus on rakendusmatemaatika osa, mis tegeleb selliste asjade uurimisega, mis võivad juhtuda või mitte juhtuda.
K: Kuidas saab tõenäosust väljendada?
V: Tõenäosust saab väljendada arvuna nulli (võimatu) ja ühe (kindel) vahel.
K: Mis on näide tõenäosuse kasutamise kohta?
V: Näide tõenäosuse kasutamise kohta on näidata, et kui visata münt õhku ja lasta sellel maanduda, siis pooltel juhtudel maandub see ühe küljega ülespoole ja pooltel juhtudel teise küljega ülespoole.
K: Kuidas arvutada tõenäosus, et kahe täringu viskamisel saadakse teatud kombinatsioon?
V: Selleks, et arvutada kahe täringu viskamise ja teatava kombinatsiooni saamise tõenäosus, korrutatakse nende kaks tõenäosust omavahel. Näiteks kui tahaksite teada, kui suur on tõenäosus saada 3 ja seejärel 5, siis oleks see 1/6 x 1/6 = 1/36.
K: Mida tähendab "saba", kui räägitakse müntidest?
V: Müntidest rääkides viitab "tagumine" külg, millel ei ole nägu või pilti.
K: Kui tõenäoline on, et kuue täringuga visates saadakse arv, mis on suurem kui kümme? V: Tõenäosust, et kuue täringuga veeretades saadakse number, mis on suurem kui kümme, saab välja arvutada matemaatika ja teaduse abil, kuid see ei ole ilmselge.
K: Mis juhtub, kui korrutada kaks tõenäosust kokku?
V: Kui te korrutate kaks tõenäosust kokku, siis arvutate tõenäosust, et mõlemad asjad juhtuvad korraga.
