Minkowski aegruum — neljamõõtmeline ruum-aeg erirelatiivsusteoorias
Minkowski aegruum: neljamõõtmeline ruum-aeg erirelatiivsusteoorias — mõõtmed, meetrika (-+++), lameda ruumiaja mõiste ja tähtsaimad põhimõtted selges keeles.
Minkowski aegruum on erirelatiivsusteooria järgi Hermann Minkowski loodud neljamõõtmeline ruumiline aeg. Sellel on neli mõõdet: kolm ruumi mõõdet (x, y, z) ja üks aja mõõde. Minkowski ruumiajal on meetrika (-+++) ja see kirjeldab lamedat pinda, kui mass puudub. Käesolevas artiklis on tavaks nimetada Minkowski ruumi aega lihtsalt ruumiajaks.
Põhimõisted
Minkowski aegruumis kombineeritakse ruum ja aeg üheks neljamõõtmeliseks manifoldiks, kus sündmuse koordinaadid on tavaliselt kirjutatud kujul (ct, x, y, z) või (t, x, y, z), sõltuvalt ühikute valikust. Siin on c valguse kiirus (vaba ruumis) ja selle kaasamine tagab, et aja mõõde on samaaegselt ühikutega võrreldav ruumimõõtmetega, kui kasutatakse ct. Tihti kasutatakse ka loogikat, kus c = 1 (loomulikud ühikud), et lihtsustada avaldisi.
Intervall ja signatuur
Minkowski ruumile omane suurus on aegruumiline intervall s^2, mis kahe lähedalasuva sündmuse vahel arvutatakse tavaliselt valemiga
s^2 = -c^2 (Δt)^2 + (Δx)^2 + (Δy)^2 + (Δz)^2.
Sellel intervallil on kolm võimalikku tähendust:
- Ajaliselt määrav (timelike): s^2 < 0 — sündmused võivad olla kausaalselt seotud ja nende vahel võib liikuda aeglasemki kehaga; eksisteerib inertsialvaatleja, kus need kaks sündmust toimuvad samas ruumipunktis, kuid eri ajal.
- Ruumi määrav (spacelike): s^2 > 0 — sündmused ei ole kausaalselt seotud; pole võimalik, et üks mõjutaks teist, sest see nõuaks odavamalt kiiremat kui valguse kiirusega liikumist.
- Valguslik (lightlike või null): s^2 = 0 — kahe sündmuse vahel liigub informatsioon ainult valguse või muu massitu osakese abil; need punktid paiknevad üksteise valguskoones.
Valguskoonus ja kausaalsus
Valguskoonus on kujutis, mis kuvab, millised sündmused on antud sündmuse suhtes kausaalselt kättesaadavad. Minevikukoone (past light cone) kuuluvad sündmused, mis võisid mõjutada antud sündmust; tulevikukoon sisaldab sündmusi, mida antud sündmus võib mõjutada. See jaotus kaitseb relativistlikku kausaalsust — põhiseadus, et mõju ei saa eellast ette jõuda kiiremini kui valgus.
Lorentzi teisendused ja invariantsus
Erirelatiivsusteooria põhialus on, et aegruumiline intervall s^2 on invariantsed kõikide inertsi süsteemide vahel. Lorentzi teisendused (sisaldavad nihkeid ja pööramisekvivalentseid teisendusi neljamõõtmelises ruumis) säilitavad intervalli väärtuse ning seeläbi valguse kiiruse ja põhisuhted. See selgitab, miks sama sündmuse kohta võivad eri vaatlejad mõõta erinevaid aja- ja pikkusmõõtmeid, kuid s^2 jääb samaks.
Meetri ja maatriksivorm
Minkowski meetrikat väljendatakse sageli maatriksina η (eta):
η_{μν} = diag(-1, +1, +1, +1).
Selle abil saab kirjutada intervalli lühidalt kujul s^2 = η_{μν} Δx^μ Δx^ν, kus indekseerimine jookseb μ = 0,1,2,3 ja Δx^0 = cΔt.
Maailmaliinid, neljavektorid ja proper-aeg
Liikuva kehale trajektoori aegruumis nimetatakse maailmaliiniks. Selle kahe lähedalasuva punkti vahel mõõdetud proper-aeg τ on inertsvaatleja jaoks keha enda jaoks mõõdetud aeg ning see on seotud intervalliga timelike juhtudel läbi seosega dτ^2 = -ds^2 / c^2. Samuti kasutatakse neljavektoreid (näiteks neljakiirus, neljajõud) relatiivsete suuruste koherentseks kujutamiseks neljamõõtmelises ruumis.
Minkowski aegruum kui erirelatiivsuse raamistik
Minkowski aegruum on erirelatiivsusteooria loogiline matemaatiline raamistik: ta on lamedapinnaline (nullligika kumulatiivne kurvatuur) ja sobib olukordade kirjeldamiseks, kus gravitatsioon on ebaoluline või puudub. Kui gravitatsiooni mõju muutub oluliseks, üldistatakse mõiste ka kõverateks aegruumideks, nagu seda teeb Üldine relatiivsusteooria, mis kirjeldab gravitatsiooni kui ruumiaja kõverust.
Ajalooline tähendus
Hermann Minkowski 1907–1908 tööd aitasid ühendada Albert Einsteini erirelatiivsusteooria geomeetrilise vaatenurgaga, näidates, et ruum ja aeg ei ole eraldiseisvad entiteedid, vaid moodustavad ühe neljamõõtmelise struktuuri. See geomeetriline lähenemine tegi hilisema üldrelatiivsusteooria arendamise loogilisemaks.
Kokkuvõte
Minkowski aegruum pakub lihtsat, kuid võimsat mudelit, kus ruum ja aeg on osa samast neljamõõtmelisest struktuurist, intervall on invariantsus, Lorentzi teisendused säilitavad selle ja valguse kiirus on absoluutne piir informatsiooni levikul. See kehtib lamedal aegruumi korral (ilma gravitatsioonita) ning on erirelatiivsusteooria keskne kontseptsioon.
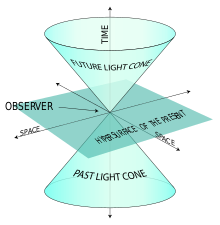
Näide valguskoonuse kohta.
Määratlus(ed)
Matemaatiline
Ruumiaega võib vaadelda kui neljamõõtmelist koordinaatsüsteemi, mille teljed on antud järgmiselt
( c t , x , y , z ) {\displaystyle (ct,x,y,z)} 
Neid võib tähistada ka järgmiselt
( x 1 , x 2 , x 3 , x 4 ) {\displaystyle (x_{1},x_{2},x_{3},x_{4})} 
Kus x 1 {\displaystyle x_{1}}
esindab c t {\displaystyle ct}
. Aega mõõdetakse valguse kiiruse ja ajakoordinaadi korrutisena, et aja mõõtühikud oleksid samad kui ruumi mõõtühikud. Ruumiaeg on kaare pikkuse diferentsiaal, mis on antud järgmiselt
d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}} 
See tähendab, et ruumiajal on meetriline tensor, mis on antud järgmiselt
g u v = [ - 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 ] {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&0&1&0\0&0&1\end{bmatrix}}} 
Nagu eespool öeldud, on ruumiaeg kõikjal lame; teatud määral võib seda pidada tasapinnaliseks.
Lihtne
Ruumiaega võib pidada "areeniks", kus toimuvad kõik sündmused universumis. Ruumiaja punkti määramiseks on vaja vaid teatud aega ja tüüpilist ruumilist orientatsiooni. Nelja dimensiooni on raske (praktiliselt võimatu) visualiseerida, kuid mõningaid analoogiaid saab teha, kasutades alljärgnevat meetodit.
Ruumiaja diagrammid
Hermann Minkowski võttis kasutusele teatava meetodi koordinaatsüsteemide graafiliseks kujutamiseks Minkowski aegruumis. Nagu paremal näha, on erinevad koordinaatsüsteemid objekti ruumilise orientatsiooni ja/või ajalise asukoha osas eriarvamusel. Nagu diagrammilt näha, on ainult üks ruumiline telg (x-telg) ja üks ajatelg (ct-telg). Vajaduse korral võib lisada veel ühe ruumilise mõõtme (y-telg); kahjuks on see mõõtmete arvu piir: nelja mõõtmega graafikute koostamine on võimatu. Minkowski aegruumi graafikute koostamise reegel on järgmine:
1) x-telje ja x'-telje vaheline nurk on antud t a n ( α ) = v c {\displaystyle tan(\alpha )={\frac {v}{c}}}
kus v on objekti kiirus.
2) Valguse kiirus läbi aegruumi teeb alati 45-kraadise nurga kummagi teljega.
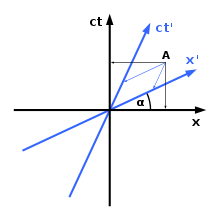
Relatiivsusteoorias omistavad mõlemad vaatlejad sündmuse A erinevatele aegadele.
Ruumiaeg üldrelatiivsusteoorias
Einstein kasutas üldises relatiivsusteoorias võrrandit
R u v - 1 2 g u v R = 8 π T u v {\displaystyle R_{uv}-{\frac {1}{2}}g_{uv}R=8\pi T_{uv}} 
Et ruumi aeg tegelikult kõveraks jääks; sellest tulenevad gravitatsiooniefektid.
Seotud leheküljed
- Ruumiaeg
- Eriline relatiivsusteooria
- Üldine relatiivsusteooria
| Ametiasutuste kontroll |
|
Küsimused ja vastused
K: Mis on Minkowski aegruum?
V: Minkowski aegruum on Hermann Minkowski loodud neljamõõtmeline ruumiline ruumiline aeg. Sellel on kolm ruumimõõdet (x, y, z) ja üks ajamõõde.
K: Milline on Minkowski aegruumi meetrika?
V: Minkowski ruumiaja meetriline signatuur on (-+++).
K: Kuidas kirjeldab Minkowski aegruumi aeg lamedat pinda?
V: Kui mass puudub, kirjeldab Minkowski ruumi aeg lamedat pinda.
K: Kas Minkowski aegruumi aegruum kehtib üldrelatiivsusteooria puhul?
V: Ei, Minkowski aegruumi kohaldatakse ainult erirelatiivsusteooria puhul. Üldine relatiivsusteooria kasutab gravitatsiooni ja kiirendatud liikumise mõju kirjeldamiseks kõverdatud ruumi aja mõistet.
K: Mitu mõõdet on Minkowski aegruumil?
V: Minkowsi aegruumil on neli mõõdet - kolm ruumi mõõdet (x, y, z) ja üks aja mõõde.
K: Kes lõi Minkowsi aegruumi mõiste?
V: Hermann Minkowksi lõi MInkowski ruumi aja mõiste.
Otsige