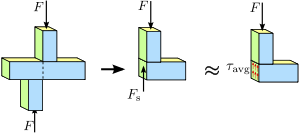Pinge (mehaanika) – definitsioon, valem ja ühikud (Pa, N/m²)

Pinge (mehaanika): definitsioon, valem ja ühikud — selgelt selgitatud σ=F/A, SI-ühik Pa (N/m²) ja psi võrdlus. Õpi, kuidas pinged põhjustavad deformatsiooni ja mõõdetakse praktikas.

Stress ehk pinge on kehale mõjuv jõud pindalaühiku kohta, mis põhjustab selle kuju muutumist või sisepingete tekkimist. Pinge kirjeldab sisemisi jõude, mis tekivad keha eri osakeste vahel, kui kehale rakendatakse väliseid jõude — need sisemised jõud on keha vastus välisele koormusele ja võivad põhjustada eraldumist, kokkusurumist või libisemist kehasisestel pindadel. Üldiselt mõistetakse pinget kui keskmist jõudu pindalaühiku kohta, mida üks osake avaldab naaberosakesele üle neid eraldava kujuteldava pinna.

Tüübid ja väljendid

Pinged jagunevad peamiselt kaheks:

Normaalpinged (tensioon ja kompressioon) — jõud on risti vaadeldava pindalaga. Ühekomponendilise (ühesuunalise, aksiaalse) normaalpinge valem on:

σ = F A {\displaystyle {\sigma }={\frac {F}{A}}} ${\sigma }={\frac {F}{A}}$

kus σ on pinge, F on jõud ja A on pindala.

Lõike- ehk nihkepinged — jõud on tangentsiaalsed (paralleelsed) vaadeldava pinnaga; neid tähistatakse tavaliselt τ ning valemiks lihtsa koguse korral τ = F_shear / A.

Ühik ja mõõtühikud

SI-süsteemis mõõdetakse jõudu njuutonites ja pindala ruutmeetrites, seega on pinge ühikuks njuuton/m² ehk N/m². Sellel on oma nimetatud ühik — paskal (sümbol Pa): 1 Pa = 1 N/m². Imperiaalsüsteemis kasutatakse sageli naela ruuttolli kohta (psi). Pinge mõõtmed on samad mis rõhul; seetõttu kasutatakse ka rõhule kehtivaid mõõtmis- ja analüüsivõtteid pingete kontekstis.

Pingete kirjeldamine 3D kohal

Kontinuumiga mehaanikas käsitletakse koormatud keha kui pidevat ainet (kontinuum), kus sisemised jõud jagunevad kogu kehamahtudes. Pingete jaotus on seega pidev funktsioon ruumis ja ajas (vt ka tükeldatud ja pideva funktsiooni mõisteid).

Kolmemõõtmelises teisendamises kirjeldatakse pingeid Cauchy pinge tensoriga σ_ij, mis on 3×3 sümmeetriline maatriks, mille komponendid annavad normaal- ja lõikepingete väärtused erinevates koordinatsioonides. Tensor võimaldab leida ka peamised pinged (σ1, σ2, σ3) — need on tensori eikoguväärtused (eigenväärtused) ja määravad suunad, kus lõikepinged on null.

Signatuur ja kasutuspraktika

Pingete märgistamisel kasutatakse erinevaid konventsioone: tihti tähistatakse tõmblevaid pingeid (tensioon) positiivsete väärtustega ja kokkusurutavaid pingeid negatiivsetena, kuid mõnes valdkonnas on vastupidine tava. Oluline on alati märkida kasutatud märgivõtted, et vältida segadust arvutustes ja spetsifikatsioonides.

Elastsus ja seos deformatsiooniga

Lineaarse elastse materjali puhul annab Hooke'i seadus lihtsa seose pingete ja deformatsioonide vahel. Ühesuunalises koormuses kehtib:

σ = E · ε, kus E on Youngi moodul ja ε on normaalne venitus (deformatsioon).
Nihe- ja lõikepinge puhul kasutatakse poorsuse (Poissoni suhtarvu ν) ja shew-mooduli G seoseid kogu maaramaks materjali reaktsiooni eri koormustel.

Üldisemalt väljendatakse lineaarset elastsust tensori kujul: σ = C : ε, kus C on elastsusmoduulide neljanda astme tensor, mis sisaldab E, G ja ν väärtusi isotroopse materjali korral.

Piirid, tugevus ja ohutuse tegurid

Materjalide hinnangul kasutatakse erinevaid tugevuse näitajaid:

Elastne piir — kus materiaal käitub elastselt ja pöördub esialgsele kujule.
Võllimispinge (yield strength) — pinge, mille juures tekib püsiv plastiline deformatsioon.
Lõhkemis- või murdeväärtus (ultimate strength) — maksimaalne pinge enne materjali lagunemist.

Disainis rakendatakse tavaliselt ohutustegurit (safety factor), et tagada konstruktsiooni vastupidavus ootamatute koormuste või defektide korral. Pingekontsentratsioonid (näiteks notsud, augud, teravad servad) võivad kohalikult oluliselt tõsta pingeid ja põhjustada ketta purunemise või väsimuse.

Analüüsimeetodid ja mõõtmine

Pingete analüüsis kasutatakse mitmeid meetodeid:

Formaalsed analüütilised valemid lihtsatele geomeetriatele (nt aksiaalne tõmbekuormus, paindumine, torsioon).
Numbrilised meetodid — eriti lõplike elementide meetod (FEM), mis võimaldab leida pingevälju keerukate kujudega ja mitme koormustingimuse korral.
Mõõtmisvõtted praktikas: venitusandurid (strain gauges), fotoelastsusmeetodid, röntgen- või neutrontomograafia ja muud nondestructive testid.

Rakendused ja näited

Pingete mõistmine on kriitiline ehituses, masinaehituses, aeronautikas, biomehaanikas jt valdkondades. Näide lihtsast arvutist: kui tõmbejõud F = 10 000 N toimib ühtlase ristlõikega A = 0,01 m² detailil, siis σ = F / A = 10 000 / 0,01 = 1 000 000 N/m² = 1 MPa.

Edasised mõisted

Täiendavad teemad, mida spetsialistid tavaliselt käsitlevad, on:

Mohr'i ring — graafiline meetod kahe- või kolmekomponendilise pingeseisundi uurimiseks ja peamiste ning maksimaalsete lõikepingete leidmiseks.
Pingete singularsused — näiteks terava murdekohaga või praguga seotud lõpmalt suured pinged teoreetilises mudelis.
Väsimine — korduvkoormuse poolt põhjustatud püsiv kahjustus, mis sõltub pingete amplituudist ja tsüklite arvust.

Kokkuvõte

Pinge on põhikogus mehaanikas, mis seob välised jõud keha sisemiste reaktsioonidega ja määrab deformatsioonide ning võimalike kahjustuste tekke. Mõistmine nõuab nii teoreetilist tausta (tensorid, elastsusmudelid) kui ka praktilisi meetodeid (mõõtmine, FEM), et tagada konstruktsioonide ohutus ja töökindlus. Kui materjal või geomeetria ei vasta koormustele, võib deformatsioon muutuda püsivaks või viia konstruktsiooni purunemiseni, mistõttu on pingete täpne hindamine disaini- ja hooldustöödes hädavajalik.

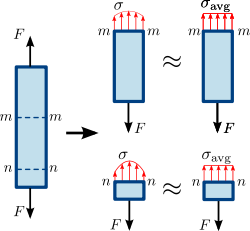
Joonis 1.4 Nihkepinge prismaatilises vardas. Pinge või jõu jaotumine varda ristlõikes ei ole tingimata ühtlane. Sellegipoolest on keskmine nihkepinge τ a v g {\displaystyle \tau _\mathrm {avg} }\,\! } $\tau _{\mathrm {avg} }\,\!$ on mõistlik lähendus.

Joonis 1.3 Normaalpinge prismaatilises (ühtlase ristlõike pindalaga sirge) vardas. Pinge või jõu jaotumine varda ristlõikes ei pruugi olla ühtlane. Kuid keskmine normaalpinge σ a v g {\displaystyle \sigma _\mathrm {avg} }\,\! } $\sigma _{\mathrm {avg} }\,\!$ võib kasutada.

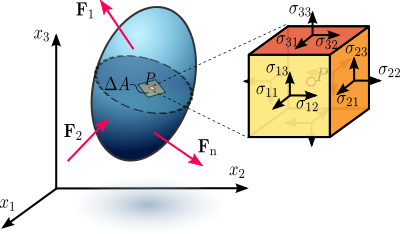
Joonis 1.1 Pinged koormatud deformeeruvas materjalikehas, mida eeldatakse kontinuumina.

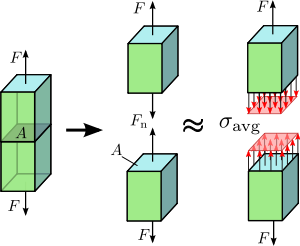
Joonis 1.2 Aksiaalpinge aksiaalselt koormatud prismaatilises vardas.

Nihkepinge

Täiendav teave: Nihkepinge

Lihtsad pinged

Mõnes olukorras saab objekti sisemist pinget kirjeldada ühe arvu või ühe vektoriga (arv ja suund). Kolm sellist lihtsat pingeolukorda on üheteljeline normaalpinge, lihtne nihkepinge ja isotroopne normaalpinge.

Üheksiaalne normaalpinge

Tõmbepinged (või pinged) on pingeseisund, mis viib pikenemiseni, st materjali pikkus kipub suurenema tõmbesuunas. Materjali maht jääb samaks. Kui kehale rakendatakse võrdseid ja vastandlikke jõude, siis nimetatakse sellest jõust tulenevat pinget tõmbepingeks.

Seetõttu suureneb ühe teljevahega materjalis pikkus tõmbepinge suunas ja teised kaks suunda vähenevad. Üheksiaalsel viisil tõmbepinget tekitavad tõmbepinged tõmbejõud. Tõmbepinged on survetugevuse vastandiks.

Otsepinge all olevad konstruktsioonielemendid on trossid, mullaankrud ja naelad, poldid jne. Paindemomendile allutatud talad võivad sisaldada nii tõmbe- kui ka survetugevust ja/või nihkepinget.

Tõmbepinget võib suurendada kuni tõmbetugevuse saavutamiseni, s.o pingete piirseisundini.

Pinged ühemõõtmelistes kehades

Kõik reaalsed objektid asuvad kolmemõõtmelises ruumis. Kui aga kaks mõõdet on teistega võrreldes väga suured või väga väikesed, võib objekti modelleerida ühemõõtmelisena. See lihtsustab objekti matemaatilist modelleerimist. Ühemõõtmeliste objektide hulka kuuluvad näiteks otsadest koormatud ja küljelt vaadeldav traaditükk ning küljelt koormatud ja lähedalt ja ristlõike kaudu vaadeldav metallplaat.

Seotud leheküljed

Tension
Painutamine

Küsimused ja vastused

K: Mis on stress?

V: Stress on kehale mõjuv jõud pindalaühiku kohta, mis põhjustab selle kuju muutumist. See on keha osakeste vaheliste sisemiste jõudude mõõt ja on keskmine jõud pindalaühiku kohta, mida üks keha osakese osake avaldab naaberosakesele üle neid eraldava kujuteldava pinna.

K: Kuidas välised jõud mõjutavad pinget?

V: Välised jõud on kas pindmised jõud või keha jõud ja need põhjustavad keha kuju deformatsiooni, mis võib viia püsiva kuju muutumiseni või konstruktsiooni purunemiseni, kui materjal ei ole piisavalt tugev.

K: Milline on ühe telje normaalse pinge valem?

V: Üheksiaalse normaalpinge valem on σ = F/A, kus σ on pinge, F on jõud ja A on pindala. SI-ühikutes mõõdetakse jõudu njuutonites ja pindala ruutmeetrites, mis tähendab, et pinge on njuutonid ruutmeetri kohta (N/m2). Siiski on olemas oma SI-ühik pinge jaoks, mida nimetatakse paskaliks (Pa), mis on võrdne 1 N/m2 . Imperiali mõõtühikutes mõõdetakse seda naelsterlingis ruuttolli kohta (psi).

K: Mida eeldab kontinuumimehaanika jõu kohta?

V: Klassikalised kontinuumimehaanika mudelid eeldavad keskmist jõudu ja ei arvesta nõuetekohaselt geomeetrilisi tegureid - see tähendab, et nad ei võta arvesse, kuidas geomeetria mõjutab seda, kuidas energia välise jõu rakendamise ajal kuhjub.

K: Kuidas võivad erinevad mudelid anda erinevaid tulemusi aine ja tahkete kehade deformatsiooni käsitlemisel?

V: Erinevad mudelid vaatlevad aine ja tahkete kehade deformatsiooni erinevalt, sest aine ja tahkete kehade omadused on kolmemõõtmelised - seega võtab iga lähenemisviis arvesse erinevaid aspekte, mis võib viia erinevate tulemusteni.

K: Kuidas käsitletakse kontinuummehaanikas koormatud deformeeruvaid kehi?

V: Kontinuummehaanika käsitleb koormatud deformeeruvaid kehi kui kontinuaale - see tähendab, et sisemised jõud jaotuvad pidevalt materiaalse keha mahus, mitte ei ole koondunud teatud punktidesse, nagu klassikaliste mudelite puhul.