Fourier' jada
Joseph Fourier ütles, et on võimalik kasutada siinuslaineid teise funktsiooni lähendamiseks. See on rida matemaatilises mõttes. Seda teooriat saab üldistada Fourier' transformatsioonile. Nende funktsioonide matemaatilist analüüsi nimetatakse Fourier' analüüsiks.
Juba 18. sajandil kasutasid matemaatikud, nagu Euler, Lagrange ja Bernoulli, sinusoidid teiste funktsioonide lähendamiseks ja modelleerimiseks. Kui Fourier avaldas 1822. aastal töö soojuse kohta, ütles ta, et sellised lähendused eksisteerivad iga sellise funktsiooni jaoks (mis on intervallile pidev). Esialgu ei usutud teda ja kulus peaaegu kümme aastat, enne kui (osa probleemi) tõestus ilmus.
Tänapäeval kasutatakse digitaalses signaalitöötluses palju Fourier' seeriaid.
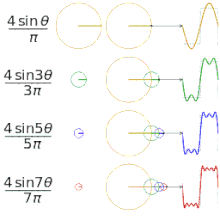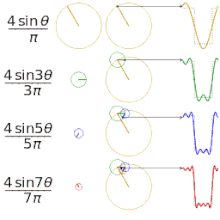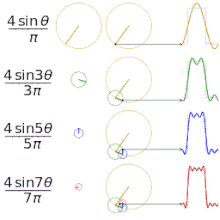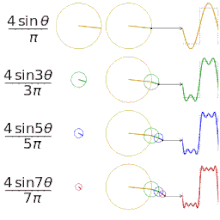
Erinevate "ruuduliste" funktsioonide lähendamine Fourier' jadade abil
Küsimused ja vastused
K: Kes oli Joseph Fourier?
V: Joseph Fourier oli prantsuse matemaatik, kes pakkus välja, et siinuslaineid saab kasutada teise funktsiooni lähendamiseks.
K: Mis on Fourier' jada?
V: Fourier' jada on jada, mis kasutab siinuslaineid teise funktsiooni lähendamiseks.
K: Mis on Fourier' teisendus?
V: Fourier' teisendus on teooria üldistus, mis kasutab siinuslaineid teise funktsiooni lähendamiseks.
K: Mis on Fourier' analüüs?
V: Fourier' analüüs on funktsioonide matemaatiline analüüs, mis kasutab siinuslaineid teise funktsiooni lähendamiseks.
K: Kes kasutas 18. sajandil sinusoidi teiste funktsioonide lähendamiseks ja modelleerimiseks?
V: Sellised matemaatikud nagu Euler, Lagrange ja Bernoulli kasutasid 18. sajandil sinusoidid teiste funktsioonide lähendamiseks ja modelleerimiseks.
K: Mida pakkus Fourier oma töös soojuse kohta 1822. aastal välja?
V: Fourier pakkus oma töös soojuse kohta 1822. aastal välja, et sellised siinuslaineid kasutavad lähendused eksisteerivad iga pideva funktsiooni jaoks antud intervalli piires.
K: Milleks kasutatakse Fourier' jada digitaalses signaalitöötluses?
V: Fourier' jadasid kasutatakse digitaalses signaalitöötluses palju signaalide lähendamiseks ja analüüsimiseks.
