Fourier' teisendus

Fourier' teisendus on matemaatiline funktsioon, mida saab kasutada signaali või laine aluseks olevate sageduste leidmiseks. Näiteks kui mängitakse akordi, saab akordi helilaine sisestada Fourier' teisendisse, et leida noodid, millest akord koosneb. Fourier' teisenduse väljundit nimetatakse mõnikord sagedusspektriks või -jaotuseks, sest see näitab sisendi sageduste spektrit. Seda funktsiooni kasutatakse palju krüptograafias, okeanograafias, masinõppes, radioloogias, kvantfüüsikas, aga ka helidisainis ja visualiseerimises.

Funktsiooni f ( x ) {\displaystyle f(x)} Fourier' teisendus f(x) järgmiselt.

F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\displaystyle F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx}} $F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx$

α {\displaystyle \alpha } $\alpha$ on sagedus

F ( α ) {\displaystyle F(\alpha )} $F(\alpha )$ on Fourier'i teisendusfunktsioon ja annab väärtuse, mis näitab, kui suur on sagedus α {\displaystyle \alpha } $\alpha$ originaalsignaalis.

e - 2 π i α x {\displaystyle e^{-2\pi i\alpha x}} $e^{-2\pi i\alpha x}$ Tähistab sisendfunktsiooni f ( x ) {\displaystyle f(x)} f(x) mähkimist ümber alguspunkti kompleksitasandis mingi sagedusega α {\displaystyle \alpha } $\alpha$

Inversne Fourier' teisendus on antud järgmiselt

f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\displaystyle f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha } $f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha$

Fourier' teisendus näitab, millised sagedused on signaalis. Võtame näiteks helilaine, mis sisaldab kolme erinevat muusikalist nooti: Kui teha selle helilaine Fourier' teisenduse graafik (kus sagedus on x-teljel ja intensiivsus y-teljel), siis on igal sagedusel tipp, mis vastab ühele muusikalisele noodile.

Erinevate amplituudide ja sagedustega kosinuste ja siinuste liitmisel saab luua palju signaale. Fourier' teisendus kujutab nende kosinuste ja siinuste amplituudid ja faasid vastavate sageduste suhtes.

Fourier-transformatsioonid on olulised, sest paljud signaalid on mõistlikumad, kui nende sagedused on eraldatud. Ülaltoodud helinäites ei ole signaali vaatlemisel aja suhtes ilmne, et signaalis on noodid A, B ja C. Paljud süsteemid teevad erinevate sagedustega erinevaid asju, nii et selliseid süsteeme saab kirjeldada selle järgi, mida nad teevad iga sagedusega. Näide on näiteks filter, mis blokeerib kõrgsagedusi.

Fourier' teisenduse arvutamine nõuab integratsiooni ja imaginaararvude mõistmist. Tavaliselt kasutatakse arvutit, et arvutada Fourier' teisendusi kõigele muule kui kõige lihtsamatele signaalidele. Kiire Fourier' teisendus on meetod, mida arvutid kasutavad Fourier' teisenduse kiireks arvutamiseks.

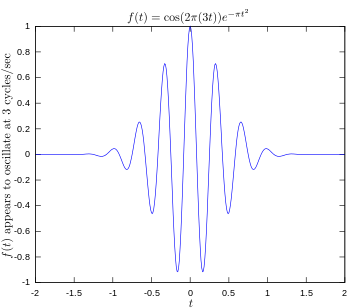
Originaalfunktsioon, mis näitab 3 hertsiga võnkuvat signaali.

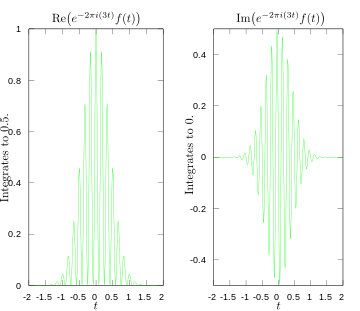
Fourier'i teisenduse integraali reaal- ja imaginaarosa 3 hertsi juures

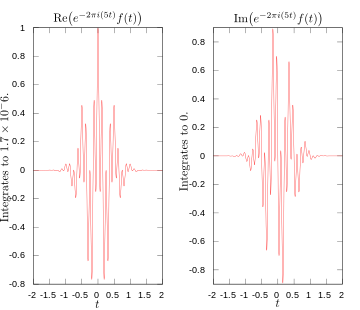
Fourier'i teisenduse integraali reaal- ja kujuteldav osa 5 hertsi juures

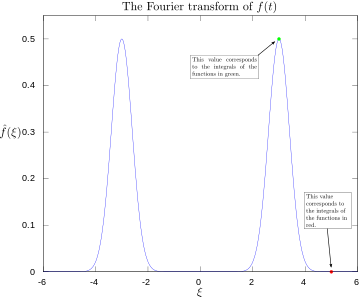
Fourier'i teisendus 3 ja 5 hertsiga märgistatud.

Küsimused ja vastused

K: Mis on Fourier' teisendus?

V: Fourier' teisendus on matemaatiline funktsioon, mida saab kasutada lainete baassageduste leidmiseks. See võtab komplekslaine ja leiab sagedused, millest see koosneb, võimaldades tuvastada noote, mis moodustavad akordi.

K: Millised on Fourier' teisenduse kasutusalad?

V: Fourier' teisendusel on palju kasutusvõimalusi krüptograafias, okeanograafias, masinõppes, radioloogias, kvantfüüsikas, aga ka helidisainis ja visualiseerimises.

K: Kuidas arvutatakse Fourier' teisendust?

V: Funktsiooni f(x) Fourier' teisendus on antud järgmiselt: F(ב) = ∫-∞+∞f(x)e-2נiבxdx, kus ב on sagedus. See tagastab väärtuse, mis näitab, kui levinud on sagedus ב algsignaalis. Inversne Fourier' teisendus on antud järgmiselt: f(x) = ∫-∞+∞F(ב)e+2נixבdב.

K: Kuidas näeb välja Fourier' teisenduse väljund?

V: Fourier' teisenduse väljundit võib nimetada kas sagedusspektriks või jaotuseks, sest see näitab sisendi võimalike sageduste jaotust.

K: Kuidas arvutid arvutavad kiiret Fourier' teisendust?

V: Arvutid kasutavad algoritmi nimega Fast Fourier Transform (FFT), et kiiresti arvutada mis tahes, kuid mitte kõige lihtsamate signaalide teisendusi.

K: Mida ei näita meile signaalide vaatlemine aja suhtes?

V: Signaalide vaatamine aja suhtes ei tee selgeks, millised noodid neis esinevad; paljud signaalid on mõistlikumad, kui nende sagedusi hoopis eraldada ja analüüsida eraldi.