Silinder – geomeetria: definitsioon, omadused, pindala ja ruumala

Silinder — definitsioon, omadused, pindala ja ruumala selgelt: valemid, näited ja illustratsioonid, et kiiresti mõista silindri geomeetriat ja arvutusi.

Autor: Leandro Alegsa

11-11-2025 13:32

Silinder on üks põhilisemaid kumeratest geomeetrilistest kujunditest, mille pinna moodustavad punktid, mis asuvad kindlal kaugusel teatavast sirgjoonest, mida nimetatakse silindri teljeks. Seda kuju võib vaadelda kui ringikujulist prisma. Nii pinda kui ka selle sees tekkivat tahket kuju võib nimetada silindriks. Silindri pindala ja ruumala on teada juba ammustest aegadest.

Diferentsiaalgeomeetrias määratletakse silindrit laiemalt kui mis tahes joonpinda, mida läbib üheparameetriline paralleelsete joonte perekond. Silindrit, mille ristlõige on ellips, parabool või hüperbool, nimetatakse vastavalt elliptiliseks silindriks, paraboolseks silindriks või hüperboolseks silindriks.

Põhiterminid ja tüübid

Teljeline (õige) silinder: generaatjooned (silindri külgpinna moodustavad sirgjooned) on risti aluse tasandiga; alused on omavahel paralleelsed ja kongruentsed ringid.
Kaldsilinder (oblique): generaatjooned on paralleelsed, kuid ei ole aluse tasandile risti — alused on siiski kongruentsed kujundid.
Ringikujuline silinder: alus on ring (sagedaseim juhtum igapäevaelus, nt konservipurgid).
Elliptiline, paraboolne, hüperboolne silinder: üldisemad kujutised, kus ristlõige telje suhtes annetatakse vastava kõvera kujuga (vt ülal).
Avatud ja suletud silinder: suletud silindril on kaks alust; avatud võib ühel või teisel juhul aluseta olla.

Olulised mõõtmed ja terminid

Raadius r: ringaluse puhul aluse ringi raadius.
Kõrgus h: telje pikkus ehk kaugus aluste vahel mõõdetuna pärisuunaliselt (perpendikulaarne aluse tasandile õige silindri puhul).
Generaatjoon (sirgjoon): silindri külgpinna moodustav sirgjoon.
Telg: sirgjoon, mille suhtes punktide kaugus on konstantne (vt esialgne määratlus).

Pindala ja ruumala (ringikujuline õige silinder)

Kui alus on ringi raadiusega r ja silindri kõrgus on h, kehtivad lihtsad valemid:

Ühe aluse pindala: A_base = π · r²
Külgpindala (ainult kõver pind, ilma alusteta): A_side = 2 · π · r · h — seda saab näha, kui külgpinna „laotada“ välja ristkülikuks mõõtmetega kõrgus h ja pikkus 2πr.
Kogu pindala (kaks alust + külgpind): A_total = 2 · π · r² + 2 · π · r · h = 2 · π · r · (r + h)
Ruumala (mahutavus): V = π · r² · h — ruumala on aluse pindala korda kõrgus.

Üksikühikud: pindala ruutühikutes (nt cm², m²), ruumala kuupühikutes (nt cm³, m³).

Üldisemad valemid ja tähelepanekud

Oblique-silindri ruumala on samuti aluse pindala korrutis kõrgusega (V = A_base · h), kus h on pärisuuline ehk aluste vaheline lühim kaugus.
Külgpindala üldisemal alusel (nt ellips) on A_side = P_base · h, kus P_base on aluse ümbermõõt (ringi puhul 2πr). Ellipsi ümbermõõdu täpne valem ei ole elementaarne ja vajab ligikaudset arvutust.
Silinder on arenenud/developable pind: õige või kaldsilindri külgpind on isomeetriline tasandiga (seda saab laotada välja kujule, mis ei veniks), seega sellel on null Gaussi kõverus (diferentsiaalgeomeetria kontekstis).

Geomeetrilised omadused ja sümmeetria

Ringikujulisel silindril on pöörd- ja peegelsümmeetria ümber telje.
Teljeline silinder on nurkade ja pindade suhtes lihtne objekt inseneritöödes: kergesti modelleeritav, mõõdetav ja tootmises kasutatav (torud, purgid, silindrilised vaaterattad jne).
Diferentsiaalgeomeetrias olulisem: silindri külgpind on ruloneeritav (developable) pind, mille geomeetrilised omadused (nt üks null-kõverus suunas generaatjoontes) eristavad seda teistest kaarjapindadest.

Näited ja rakendused

Põhiline igapäevane näide: konservipurgid, joogipudelid, torustikud — kõik kasutavad ringikujulist silindrit.
Inseneritöös kasutatakse silindrit surveanumates, mootori silindrites ja hammasrataste telgede ümbruses.
Matemaatikas ja füüsikas kasutatakse silindrit integratsiooniülesannetes, mahu- ja pindalade arvutustes ning ruumanalüüsis.

Lühike kokkuvõte

Silinder on lihtne, aga praktiline geomeetriline keha, mida võib vaadelda nii elementaarselt (ringikujuline prisma) kui ka diferentsiaalgeomeetriliselt (pind, mida läbib paralleelsete joonte perekond). Valemid pindala ja ruumala jaoks on intuitiivsed: ruumala = aluse pindala × kõrgus, ning külgpind on aluse ümbermõõdu ja kõrguse korrutis (ringi puhul 2πr·h).

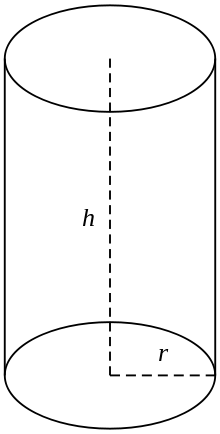
Parempoolne ümmargune silinder

Üldine kasutamine

Üldkasutuses peetakse silindri all silmas täisnurksete ümmarguste silindrite lõplikke lõikeid, st silindrit, mille tekitavad jooned on risti alustega ja mille otsad on suletud, moodustades kaks ringikujulist pinda, nagu on näidatud joonisel (paremal). Kui silindri raadius $on r$ ja pikkus (kõrgus) h, siis on selle ruumala antud järgmiselt:

$V$ $= πrh 2$

ja selle pindala on:

ülemise osa pindala $(πr 2) +$
põhja pindala $(πr 2) +$
külgpindala ( $2πrh$ ) $.$

Seetõttu on pindala ilma ülemise või alumise (külgmise) pindalata:

$A$ $= 2πrh$ .

Ülemine ja alumine pindala on:

$A$ $= 2πr 2 + 2πrh = 2πr(r + h)$ .

Antud ruumala puhul on väikseima pindalaga silindri pindala $h = 2r$ . Antud pindala korral on suurima ruumalaga silindril $h = 2r$ , st silinder mahub kuubikusse (kõrgus = läbimõõt).

Köide

Võttes täisnurkse ümmarguse silindri kõrgusega $h$ ühikut ja aluse raadiusega $r$ ühikut, mille koordinaatteljed on valitud nii, et alguspunkt on ühe aluse keskpunktis ja kõrgus mõõdetakse piki positiivset x-telge. Tasandilise lõigu pindala alguspunktist $x$ ühiku kaugusel on $A (x)$ ruutühikut, kus

A ( x ) = π r {\displaystyle2 A(x)=\pi r^{2}} $A(x)=\pi r^{2}$

või

A ( y ) = π r {\displaystyle2 A(y)=\pi r^{2}} $A(y)=\pi r^{2}$

Mahu element on täisnurkne silinder, mille aluspindala on $Aw i$ ruutühikut ja paksus $Δx i$ ühikut. Seega, kui V kuupmeetriühikut on Riemanni summade järgi õige ümmarguse silindri ruumala,

V o l u m e o f c y l i n d e r = lim | | | Δ → | 0| ∑ i = n 1A ( w i ) Δ i x {\displaystyle \mathrm {Volume\;of\;cylinder} =\lim _{||\Delta \to 0|||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x} $\mathrm {Volume\;of\;cylinder} =\lim _{||\Delta \to 0||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x$

= ∫ h0 A ( y ) d2 y {\displaystyle =\int _{0}^{h}A(y)^{2}\,dy} $=\int _{0}^{h}A(y)^{2}\,dy$

= ∫ h0 π r d2 y {\displaystyle =\int _{0}^{h}\pi r^{2}\,dy} $=\int _{0}^{h}\pi r^{2}\,dy$

= π r h 2{\displaystyle =\pi \,r^{2}\,h\,} $=\pi \,r^{2}\,h\,$

Kasutades silindrilisi koordinaate, saab ruumala arvutada integreerimise teel üle

= ∫ h0 ∫ π02 ∫ r0 s d s d ϕ d z {\displaystyle =\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz} $=\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz$

= π r h 2{\displaystyle =\pi \,r^{2}\,h\,} $=\pi \,r^{2}\,h\,$

Silindriline ristlõige

Silindrilõiked on silindrite ja tasapindade ristumiskohad. Parempoolse ümmarguse silindri puhul on neli võimalust. Silindrit puudutav tasapind, mis ristub silindriga ühel sirgjoonel. Liigutatuna, olles paralleelne iseendaga, tasand kas ei ristu silindriga või lõikab seda kahes paralleelses sirgjoontes. Kõik muud tasapinnad lõikavad silindrit ellipsina või, kui nad on risti silindri teljega, ringina.

Muud silindritüübid

Elliptiline silinder ehk cylindroid on kvadriline pind, mille võrrand kartesiaanlikes koordinaatides on järgmine:

( x a ) +2 ( y b ) =21 . {\displaystyle \left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.} $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.$

See võrrand kehtib elliptilise silindri kohta, mis on tavalise ümmarguse silindri ( $a = b$ ) üldistus. Veelgi üldisem on üldistatud silinder: ristlõige võib olla mis tahes kõver.

Silinder on degeneratiivne kvadriks, sest vähemalt üks koordinaat (antud juhul $z)$ ei esine võrrandis.

Viltuse silindri ülemine ja alumine pind on teineteisest nihkes.

On ka muid ebatavalisi silindritüüpe. Need on kujuteldavad elliptilised silindrid:

( x a ) +2 ( y b ) = 2- 1{\displaystyle \left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1}} $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1$

hüperboolne silinder:

( x a ) 2- ( y b ) = 2{\displaystyle1 \left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1} $\left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1$

ja paraboolne silinder:

x +2 a2 y =0 . \displaystyle x^{2}+2ay=0.\,} $x^{2}+2ay=0.\,$

Elliptiline silinder

Projektiivses geomeetrias on silinder lihtsalt koonus, mille tipp asub lõpmatuses, mis vastab visuaalselt perspektiivsele silindrile, mis näib olevat koonus taeva suunas.

Projektiivne geomeetria

Projektiivses geomeetrias on silinder lihtsalt koonus, mille tipp asub lõpmatuses.

See on kasulik degeneratiivsete koonuste määratlemisel, mis nõuavad silindriliste koonuste käsitlemist.

Küsimused ja vastused

K: Mis on silinder?

V: Silinder on kolmemõõtmeline geomeetriline kuju, mille pinna moodustavad punktid, mis asuvad kindlal kaugusel teatavast sirgjoonest, mida nimetatakse silindri teljeks. Seda võib mõelda kui ringprisma ja nii pinda kui ka sisemuses tekkivat tahket kuju võib nimetada silindriks.

Küsimus: Kui kaua on inimesed teadnud silindrite pindala ja ruumala?

V: Silindrite pindala ja ruumala on teada juba ammustest aegadest.

K: Mis on elliptiline, paraboolne ja hüperboolne silinder?

V: Elliptilised, paraboolsed ja hüperboolsed silindrid on silindrid, mille ristlõige on vastavalt ellips, parabool või hüperbool.

K: Kuidas on silinder defineeritud diferentsiaalgeomeetrias?

V: Diferentsiaalgeomeetrias on silinder laiemalt defineeritud kui joonpind, mida läbib üheparameetriline paralleelsete sirgete perekond.

K: Mida tähendab see, et midagi on "joonestatud"?

V: "Joonestatud" tähendab, et sellele on ühel või teisel viisil joonistatud sirgjooned.

K: Kas on olemas ainult ühte tüüpi silinder?

V: Ei, on olemas palju erinevaid silindritüüpe, näiteks elliptilised, paraboolsed ja hüperboolsed silindrid, mis kõik on erineva ristlõikega.

Otsige