Algoritm

Algoritmide võrdlemine

Probleemi lahendamiseks on tavaliselt rohkem kui üks viis. Teatud roa valmistamiseks võib olla palju erinevaid retsepte, mis näevad küll erinevad välja, kuid lõppkokkuvõttes maitsevad samamoodi. Sama kehtib ka algoritmide kohta. Mõned neist viisidest on siiski paremad kui teised. Kui retsept vajab palju keerulisi koostisosi, mida teil ei ole, ei ole see nii hea kui lihtne retsept. Kui me vaatleme algoritme kui probleemide lahendamise viise, tahame sageli teada, kui kaua kuluks arvutil aega, et lahendada probleem konkreetse algoritmi abil. Kui me kirjutame algoritme, tahame, et meie algoritm võtaks võimalikult vähe aega, et saaksime oma probleemi võimalikult kiiresti lahendada.

Mõned retseptid on toiduvalmistamisel keerulisemad kui teised, sest nende valmistamine võtab rohkem aega või on rohkem asju, mida tuleb jälgida. Sama kehtib ka algoritmide kohta ja algoritmid on paremad, kui neid on arvutil lihtsam teha. Seda, mis mõõdab algoritmi raskust, nimetatakse keerukuseks. Kui me küsime, kui keeruline on mingi algoritm, tahame sageli teada, kui kaua võtab arvutil aega lahendada probleem, mida me tahame, et ta lahendaks.

Sorteerimine

See on näide algoritmist, mis sorteerib värvidega kaardid samavärvilistesse kuhjadesse:

1. Korja kõik kaardid üles.
2. Valige oma käest kaart ja vaadake, mis värvi kaart on.
3. Kui selle värvi kaartide hunnik on juba olemas, pane see kaart sellele hunnikule.
4. Kui selle värvi kaartide hunnikut ei ole, tee uus hunnik ainult selle värvi kaartidest.
5. Kui teie käes on veel kaart, minge tagasi teise sammu juurde.
6. Kui teie käes ei ole veel ühtegi kaarti, siis kaardid sorteeritakse. Te olete valmis.

Sorteerimine numbrite järgi

Need on näited algoritmide kohta, mis sorteerivad paljude erinevate numbritega kaartide virna nii, et numbrid oleksid järjekorras.

Mängijad alustavad kaardipakiga, mida ei ole sorteeritud.

Esimene algoritm

See algoritm läbib kaardipaki ühe kaardi korraga. Seda kaarti võrreldakse virna järgmise kaardiga. Pange tähele, et see positsioon muutub alles sammus 6. Seda algoritmi nimetatakse mulli sorteerimiseks. See on aeglane.

1. Kui kaardipinu on tühi või sisaldab ainult ühte kaarti, on see sorteeritud; olete valmis.
2. Võtke kaardipakk. Vaadake virna esimest (ülemist) kaarti.
3. Kaart, mida te vaatate, on kaart A. Kaardi A praegune asukoht on virnas P.
4. Kui pärast kaarti A ei ole virnas enam ühtegi kaarti, minge sammu 8 juurde.
5. Järgmine kaart virnas on kaart B.
6. Kui kaardil B on väiksem number kui kaardil A, vahetage kaartide A ja B positsioonid. Kui vahetate kaarte, ärge muutke positsiooni P.
7. Kui pärast positsiooni P on virnas veel üks kaart, vaadake seda; minge tagasi sammu 3 juurde.
8. Kui te ei vahetanud ühegi kaardi positsiooni viimases mängus, siis olete lõpetanud; kaardipinu on sorteeritud.
9. Vastasel juhul minge tagasi sammu 2 juurde.

Näide samm-sammult

Võtame kaardipaki numbritega "5 1 4 2 8" ja sorteerime selle väikseimast numbrist suurimani, kasutades seda algoritmi. Igal sammul võrdleb algoritm paksus kirjas olevaid elemente. Kaartide virna ülemine osa on vasakul pool.

Esimene läbimine:
( 5 1 4 2 8 ) → \displaystyle \to } ( 1 5 4 2 8 ) Siin võrdleb algoritm kahte esimest elementi ja vahetab need.
( 1 5 4 2 8 ) → {\displaystyle \to } ( 1 4 5 2 8 )
( 1 4 5 2 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 ) Need elemendid on juba järjekorras, seega algoritm ei vaheta neid.
Teine läbimine:
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } {\displaystyle \to } ( 1 2 4 5 8 )
Nüüd on kaartide virn juba sorteeritud, kuid meie algoritm ei tea seda. Algoritmil on vaja ühte tervet käiku ilma vahetuseta, et teada saada, et see on sorteeritud.
Kolmas läbimine:
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } {\displaystyle \to } ( 1 2 4 5 8 )
Lõpuks on massiiv sorteeritud ja algoritm võib lõpetada.

Ajalugu

See on kergesti arusaadav sorteerimise algoritm. Arvutiteadlased nimetasid seda mulli sorteerimiseks, sest väiksemad elemendid tõusevad üles, muutes oma positsiooni iga kord. Kahjuks ei ole see algoritm väga hea, sest sorteerimiseks kulub palju aega (palju läbikäike läbi kaardihunniku).

Teine algoritm

See algoritm kasutab teist ideed. Mõnikord on probleemi lahendamine keeruline, kuid probleemi saab muuta nii, et see koosneb lihtsamatest probleemidest, mida on lihtsam lahendada. Seda nimetatakse rekursiooniks. Seda on raskem mõista kui esimest näidet, kuid see annab parema algoritmi.

Põhiidee

1. Kui virnas ei ole ühtegi kaarti või on seal ainult üks kaart, on see sorteeritud ja te olete valmis.
2. Jagage kaardipakett kaheks umbes ühesuuruseks pooleks. Kui kaartide arv on paaritu, on ühes kahest virnast üks kaart rohkem kui teises.
3. Sorteerige mõlemad virnad selle algoritmi abil (alustage mõlema virna puhul selle nimekirja punktist 1).
4. Ühendage kaks sorteeritud virna kokku, nagu allpool kirjeldatud.
5. Tulemuseks on sorteeritud kaardipakk. Te olete valmis.

Kahe virna ühendamine

See töötab kahe kaardipakiga. Üks neist kannab nime A, teine B. On olemas kolmas, alguses tühi virn, mille nimi on C. Lõpuks sisaldab see tulemust.

1. Kui kas virn A või virn B on tühi, asetage kõik selle virna kaardid, mis ei ole tühi, virna C peale; olete valmis, virn C on ühendamise tulemus. (Märkus: võtke kogu virn ja pange see virnale C; kui teete seda kaartide kaupa, muutub järjekord ja see ei toimi nii, nagu peaks).
2. Vaadake virna A ja virna B ülemisi kaarte. Pange see, mille number on väiksem, virna C peale. Kui virnas C ei olnud ühtegi kaarti, siis nüüd on seal üks kaart.
3. Kui kas virnas A või virnas B on veel kaarte, minge nende sorteerimiseks tagasi sammu 1 juurde.

Ajalugu

John von Neumann töötas selle algoritmi välja 1945. aastal. Ta ei nimetanud seda numbrite järgi sorteerimiseks, vaid Mergesortiks. See on väga hea sorteerimisalgoritm, võrreldes teistega.

Kolmas algoritm

Esimese algoritmi puhul võtab kaartide sorteerimine palju kauem aega kui teise puhul, kuid seda on võimalik parandada (paremaks teha). Vaadates mullisorteerimist, võib märgata, et suurte numbritega kaardid liiguvad virna ülaosast üsna kiiresti, kuid madala numbriga kaartidel, mis on virna allosas, võtab tõusmine (ülespoole liikumine) kaua aega. Esimese algoritmi parandamiseks on siin idee:

Selle asemel, et võrrelda kahte kõrvuti olevat kaarti, valitakse alguses üks "eriline" kaart. Seejärel võrreldakse kõiki teisi kaarte selle kaardiga.

1. Alustame virna A. On veel kaks virna B ja C, mis luuakse hiljem.
2. Kui virnas A ei ole ühtegi kaarti või on ainult üks kaart, on sorteerimine lõpetatud.
3. Kaart valitakse virnast A, võimaluse korral juhuslikult. Seda nimetatakse pivotiks.
4. Kõik ülejäänud kaardid virnast A võrreldakse selle pöördepunktiga. Väiksema numbriga kaardid lähevad virna B, sama või suurema numbriga kaardid lähevad virna C.
5. Kui virnades B või C on kaarte, tuleb need virnad sorteerida sama algoritmi abil (alustage nii virna B kui ka virna C puhul selle nimekirja positsioonist 1).
6. Tehtud. Sorteeritud kaardipinu on kõigepealt sorteeritud virn B, seejärel pivot ja seejärel sorteeritud virn C.

Ajalugu

Selle algoritmi töötas 1960. aastal välja C. A. R. Hoare. See on tänapäeval üks kõige laialdasemalt kasutatavaid sorteerimisalgoritme. Seda nimetatakse Quicksortiks.

Animatsioon, mis näitab, kuidas mulli sorteerimine toimib


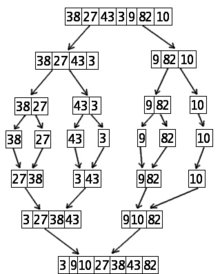
7 numbri sorteerimine teise numbrite järgi sorteerimise algoritmi (Mergesort) abil


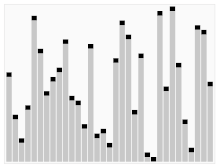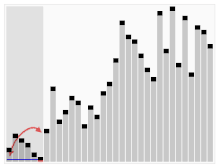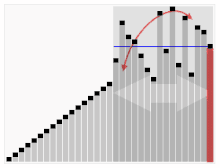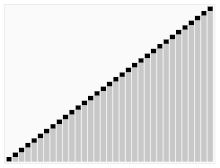
Kolmas algoritm kaartide sorteerimiseks. Pöördepunktiks valitakse punase ribaga element. Alguses on see element kõige paremal. Seda algoritmi nimetatakse Quicksort'iks.

Algoritmide koostamine

Kui mängijatel on värvide ja numbritega kaardid, saavad nad neid sorteerida värvide ja numbrite järgi, kui nad teevad algoritmi "sorteerimine värvide järgi", seejärel teevad algoritmi "sorteerimine numbrite järgi" igale värvilisele virnale, seejärel panevad virnad kokku.

Numbrite järgi sorteerimise algoritme on keerulisem teha kui värvide järgi sorteerimise algoritmi, sest neid samme võib olla vaja teha mitu korda uuesti. Võib öelda, et numbrite järgi sorteerimine on keerulisem.

Seotud leheküljed

• Eukleidese algoritm leiti üle 2000 aasta tagasi. Sellega on võimalik leida kahe arvu suurim ühine jagaja.