Fraktal

Fraktaal on mis tahes muster, mis pildina vaadatuna annab pildi, mida suurendades tekib ikka veel sama pilt. Seda saab lõigata osadeks, mis näevad välja nagu väiksemad versioonid pildist, millest alustati. Sõna fraktaal moodustas Benoît Mandelbrot 1975. aastal ladinakeelsest sõnast fractus, mis tähendab "purunenud" või "murdunud". Lihtne näide on puu, mis hargneb väiksemateks harudeks ja need harud omakorda väiksemateks harudeks jne. Fraktaalid ei ole mitte ainult ilusad, vaid neil on ka palju praktilisi rakendusi.

Sierpinski kolmnurk, pärast 7 iteratsiooni.

Mandelbrot'i hulk on kuulus näide fraktalist.

Näited

Fraktaleid on palju erinevaid, mis on tehtud väga erineval viisil. Üks näide on Sierpinski kolmnurk, kus suure kolmnurga sees on lõpmatult palju väikseid kolmnurki. Teine näide on Mandelbrot' hulk, mis on nime saanud Benoît Mandelbrot' järgi. Sierpinksi kolmnurk on konstrueeritud mustrite abil, kuid Mandelbrot' hulk põhineb võrrandil.

Looduses on ka palju looduslikke näiteid fraktaalidest, sealhulgas puud, lumehelbed, mõned köögiviljad ja rannikualad.

Kochi kõver

Kochi kõver on lihtne näide fraktalist. Alustame kõigepealt sirgjoone osast, mida nimetatakse sirgjoonesegmendiks. Lõigake sirge kolmeks ühesuuruseks tükiks. Vabanege nende tükkide keskelt ja pange sisse kolmnurga ülemine osa, mille küljed on sama pikad kui välja lõigatav osa. Nüüd on meil 4 sirgussegmenti, mis puutuvad otsadest kokku. Nüüd saame teha seda, mida tegime äsja esimese segmendi puhul iga 4 tükiga. Nüüd saame teha sama asja uuesti ja uuesti kõigi lõikudega, mis meil lõpuks on. Teeme seda nüüd igavesti ja vaatame, mis meil lõpuks välja tuleb.

Kochi kõvera pikkus on lõpmatus ja Kochi kõvera pindala on null. See on üsna kummaline. Joone lõik (mõõtmega 1) võib olla pikkusega 1, kuid tema pindala on 0. Ruut pikkusega 1 ja laiusega 1 (mõõtmega 2) on pindalaga 1 ja pikkusega lõpmatus.

Sarnasuse mõõde

Niisiis, Kochi kõver näib olevat suurem kui midagi mõõtmega 1 ja väiksem kui midagi mõõtmega 2. Sarnasuse dimensiooni mõte on anda mõõde, mis annab parema ettekujutuse fraktaalide pikkusest või pindalast. Niisiis, Kochi kõvera puhul tahame mõõdet vahemikus 1 ja 2.

Kochi kõverat saab lõigata neljaks tükiks, millest igaüks on 1 3 {\displaystyle {\frac {\frac {1}{3}}} ${\frac {1}{3}}$ originaali suurusest. Nimetame fraktaali tükeldatavate osade arvu N {\displaystyle N} $N$ ja suuruse erinevust B {\displaystyle B} $B$ . Paneme need võrrandisse:

log N - log B {\displaystyle {\frac {\log N}{-\log B}}} ${\frac {\log N}{-\log B}}$

Kus log {\displaystyle \log } $\log$ on arvu logaritm. See arv on fraktaali Hausdorffi dimensioon. Kochi kõveras on see log 4 - log 1 3 = 1,2619... {\displaystyle {\frac {\log 4}{-\log {\frac {1}{3}}}}=1.2619... } ${\frac {\log 4}{-\log {\frac {1}{3}}}}=1.2619...$ nagu me tahtsime.

Kochi kõver on üks lihtsamaid fraktaalseid kujundeid ja seega on selle mõõtmeid lihtne välja arvutada. Selle sarnasuse mõõde ja Hausdorffi mõõde on mõlemad samad. See ei kehti keerukamate fraktaalide kohta.

Koch lumehelbeke

Kochi lumehelves (või Kochi täht) on sama, mis Kochi kõver, ainult et see algab võrdkülgse kolmnurgaga, mitte sirgjoonega.

Kuidas teha Kochi kõverat

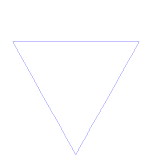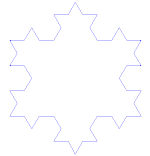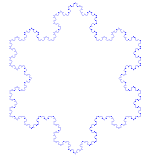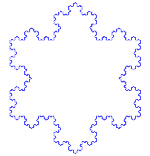
Kasutab

Fraktaalidel on palju rakendusi näiteks bioloogias (kopsud, neerud, südame löögisageduse muutlikkus jne...), maavärinates, rahanduses, kus see on seotud nn raskete sabajagudega, ja füüsikas. See näitab, et fraktaale tuleks uurida, et mõista, miks fraktaalid on looduses nii sagedased.

Mõned fraktaalid on olemas ainult kunstilistel põhjustel, kuid teised on väga kasulikud. Fraktalid on väga tõhusad raadioantennide kujundid ja neid kasutatakse arvutikiipides, et ühendada tõhusalt kõik komponendid. Ka rannajoone võib pidada fraktaalideks.

Küsimused ja vastused

K: Mis on fraktaal?

V: Fraktal on mis tahes muster, mis pildina vaadatuna annab pildi, mis suumimisel jääb samaks.

K: Kellele on omistatud mõiste "fraktal" leiutamine?

V: Benoît Mandelbrot'ile omistatakse mõiste "fraktal" kasutuselevõtt 1975. aastal.

K: Milline on sõna "fraktal" etümoloogia?

V: Sõna "fraktaal" on tuletatud ladinakeelsest sõnast "fractus", mis tähendab "purunenud" või "murdunud".

K: Kas fraktaale saab lõigata osadeks?

V: Jah, fraktaale saab lõigata osadeks, mis näevad välja nagu väiksemad versioonid pildist, millest nad alguse said.

K: Kas te oskate tuua näite fraktali kohta?

V: Lihtne näide fraktali kohta on puu, mis hargneb väiksemateks harudeks ja need harud omakorda väiksemateks harudeks jne.

K: Millised praktilised rakendused on fraktaalidel?

V: Fraktaalidel on palju praktilisi rakendusi, näiteks arvutigraafikas, meditsiinis, füüsikas ja rahanduses.

K: Miks on fraktaalid olulised?

V: Fraktalid on olulised, sest need aitavad meil mõista keerulisi loodusnähtusi ning luua täpsemaid mudeleid ja simulatsioone.