Kuldlõige
Ühe arvu a ja teise väiksema arvu b puhul leitakse nende kahe arvu suhe, jagades need omavahel. Nende suhe on a/b. Teine suhe leitakse kahe arvu liitmisel a+b ja selle jagamisel suurema arvuga a. Uus suhe on (a+b)/a. Kui need kaks suhet on võrdsed ühe ja sama arvuga, siis nimetatakse seda arvu kuldseks suhteks. Kreeka täht φ {\displaystyle \varphi } 
(phi) kasutatakse tavaliselt kuldlõike nimetusena.
Näiteks kui b = 1 ja a/b = φ {\displaystyle \varphi } , siis a = φ {\displaystyle \varphi } . Teine suhe (a+b)/a on siis ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi } 
. Kuna need kaks suhet on võrdsed, siis on see tõsi:
φ = φ + 1 φ {\displaystyle \varphi ={\frac {\varphi +1}{\varphi }}
Üks viis selle numbri kirjutamiseks on
φ = 1 + 5 2 {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}
5 {\displaystyle {\sqrt {5}}
on nagu iga arv, mis iseendaga korrutades annab 5 (või mis arv korrutatakse): 5 × 5 = 5 {\displaystyle {\sqrt {5}}\times {\sqrt {5}}=5}
.
Kuldne suhe on irratsionaalne arv. Kui inimene üritab seda kirjutada, siis see ei peatu kunagi ega tee kunagi mustrit, vaid algab nii: 1,6180339887... Oluline asi selle arvu juures on see, et inimene saab sellest arvust 1 maha arvata või sellega 1 jagada. Mõlemal juhul jätkab see number ikkagi ja ei peatu kunagi.
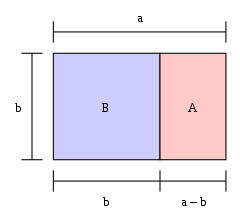
Kuldne ristkülik
Kui ristküliku pikkus jagatud selle laiusega on võrdne kuldlõikega, siis on see ristkülik "kuldne ristkülik". Kui kuldse ristküliku ühest otsast lõigatakse välja ruut, siis on teine ots uus kuldne ristkülik. Pildil on suur ristkülik (sinine ja roosa koos) kuldne ristkülik, sest a / b = φ {\displaystyle a/b=\varphi } 
. Sinine osa (B) on ruut. Roosa osa üksi (A) on teine kuldne ristkülik, sest b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi } 
. Suur ristkülik ja roosa ristkülik on sama kujuga, kuid roosa ristkülik on väiksem ja pööratud.
Suur ristkülik BA on kuldne ristkülik; see tähendab, et suhe b:a on 1: φ \displaystyle \varphi } . Iga sellise ristküliku puhul, ja ainult sellise proportsiooniga ristkülikute puhul, kui me eemaldame ruudu B, jääb alles teine kuldne ristkülik A, st sama proportsiooniga kui algne ristkülik.
Fibonacci numbrid
Fibonacci numbrid on numbrite nimekiri. Inimene saab leida järgmise numbri nimekirjas, kui ta liidab kaks viimast numbrit kokku. Kui inimene jagab loendis oleva arvu sellele eelnenud arvuga, läheneb see suhe üha enam kuldsele lõigule.
| Fibonacci arv | jagatud eelneva arvuga | suhe |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| φ \displaystyle \varphi } | = 1.6180... |
Kuldne suhe looduses
Looduses kasutatakse kuldset lõiku sageli lehtede või lillede paigutamisel. Need kasutavad kuldset nurka, mis on ligikaudu 137,5 kraadi. Sellise nurga all paigutatud lehed või lilled kasutavad kõige paremini päikesevalgust.
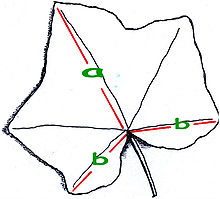
Hariliku muraka leht, millel on kujutatud kuldne suhe
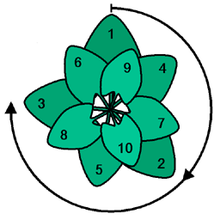
Kuldse nurga kasutamine kasutab optimaalselt päikese valgust. See on vaade ülaltpoolt.
Küsimused ja vastused
K: Mis on kahe arvu suhe?
V: Kahe arvu suhe leitakse nende jagamisel, seega oleks suhe a/b.
K: Kuidas saab leida teise suhtarvu?
V: Teise suhte saab leida, kui liita kaks arvu kokku ja seejärel jagada see summa suurema arvuga a. See uus suhe oleks (a+b)/a.
K: Kuidas nimetatakse seda, kui need kaks suhtarvu on võrdsed?
V: Kui need kaks suhtarvu on võrdsed, nimetatakse seda kuldseks suhtarvuks. Seda kujutatakse tavaliselt kreeka tähega צ või phi.
K: Kui b = 1 ja a/b = צ , mida tähendab see a jaoks?
V: Kui b = 1 ja a/b = צ , siis tähendab see, et ka a = צ.
K: Kuidas saab seda arvu kirjutada?
V: Üks võimalus seda arvu kirjutada on צ = 1 + 5 / 2 = 1,618...
K: Mida tähendab see, kui sellest arvust lahutada 1 või jagada sellega 1?
V: Kui sellest lahutad 1 või jagad sellega 1, saad tagasi sama arvu - teisisõnu, mõlemad võrduvad kuldlõikega.
K: Kas kuldlõige on irratsionaalne arv?
V: Jah, kuldne suhe on irratsionaalne arv, mis tähendab, et kui keegi üritab seda välja kirjutada, siis ei tule kunagi lõppu ega mingit mustrit - ainult algab midagi sellist nagu "1,6180339887...".