Valguskell — relatiivsusteooria näide ja aeglaienemise selgitus

Valguskell selgitab relatiivsusteooriat ja aeglaienemist lihtsa näite kaudu — visuaalne juhend, selged võrrandid ja igapäevased võrdlused, mis teevad Einsteini ideed arusaadavaks.

Valguskell on lihtne ja selge mõttekatse, mis näitab erilise relatiivsusteooria põhijooni. Kell on üles ehitatud nii, et ühelt poolt posti alt lähtuv valgusevihu peegeldub posti otsas olevast peeglist tagasi ning see tagasipöördumine vallandab jälle uue välgu. Kell loendab, mitu välku selle protsessi ajal tekib. Maalt vaadates, kui väga kiire kosmoselaev lendab ja selle pardal on samasugune valguskell, näib kosmoselaeva kell tiksumisest aeglasem — seda nähtust nimetatakse ajalaiuseks (ajalaienemine).

Enne valguskella vaatlust mõelgem lühemalt teisest suhtelisuse näitest. Kujutage ette korvpallurit, kes trambib palli suure kaubalennuki kabiinis ja liigub lennukiga samas suunas. Lennuki pardal paistab ühe trambitõmbe ajal palli liikumine olevat ainult mõned meetrid. Aga Maa pealt vaadates on samal ajavahemikul pall liikunud ka lennuki liikumise võrra — seega palju suurema maa-pinna suhtes mõõdetud vahemaa. See illustreerib, et samale sündmusele (palli põrkumine) vastavad erinevad koordinaadid ja ajad erinevates referentsraamistikus.

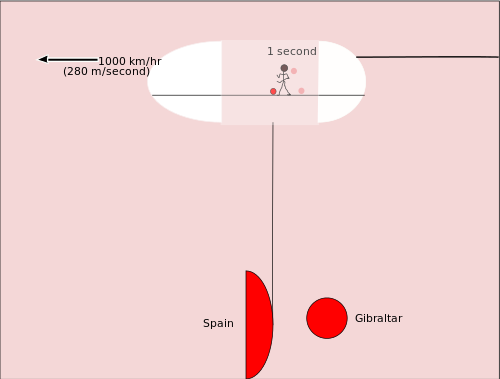
Kuidas valguskell töötab (mitte-relativistlik vaatlus)

Valguse kiirus c on looduses konstantne; teadlased tähistavad seda tähega c. Kui valguskell on paika pandud nii, et posti pikkus (alusest peani) on a, läbib valgustilk üles ja tagasi kokku vahemaa d = 2a. Kui vaatleja on kellaga koos (st kell on vaatleja jaoks liikumatu), siis tavaline üks "tik" võtab aja t = d / c = 2a / c. Näiteks lihtsustuseks oletame posti pikkuseks pool kilomeetrit (a = 0,5 km), siis läbitud vahemaa ühe tikuga on 1 km ja aeg t = 1 km / (300 000 km/s) ≈ 0,00000333 s (3,33·10^-6 s). Selline kell "tiksub" väga tihti, sest valgus liigub väga kiiresti.

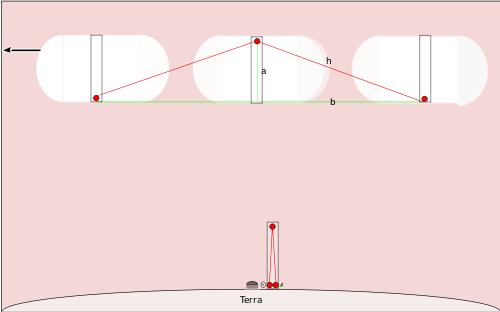
Valguskell ja liikuva kosmoselaeva näide — relatiivne aeglaienemine

Vaadeldes sama kella, mis asub nüüd kiiresti liikuvatel kosmoselaeval, märkame olulist muutust. Maa pealt vaatlejad näevad, et kella peegli ja valgusallika liikumise tõttu ei liigu valgus otse vertikaalselt üles-alla, vaid diagonaalselt (joonisel tähistatud hüpotenuusiga). Kui kosmoselaev liigub horisontaalsuunas kiirusega r, peab valgus kulgema pikema trajektoori, et jõuda peeglist tagasi alusse, seega kulub selleks rohkem aega kui kella pardal mõõdetud t.

Oluline on siin kaks fakti:

• Valguse kiirus c on kõigi vaatlejate jaoks sama.
• Kella põhja ja tipu vaheline (pardi sees olev) kaugus a on sama (see on kella enda "omamõõt" ehk proper length kella jaoks, mis liigub koos kosmoselaevaga).

Maa pealt vaadeldes liigub astmelik valgus ülespoole diagonaalset rada. Kui ühe tikuga kulunud aeg Maa vaatleja jaoks on t', siis kosmoselaev on selle ajal liikunud horisontaalselt kauguse r t' (kogu üles-alla protsessi jaoks); aga üles- või allasuuna poole liikudes vastab sellest pooleline nihe r t'/2. Pythagorase teoreemi abil saab õhukese kolonni jaoks, kus diagonaali pikkus on h:

h = √(a² + (r t'/2)²)

Valguse kogu teekond ühe tikiga (üles ja tagasi) on d = 2h = 2 √(a² + (r t'/2)²). Samas kehtib valguse puhul d = c t' (sest valgus läbib selle teekonna aja t' jooksul kiirusega c). Seega võrdleme kahe avaldisega:

c t' = 2 √(a² + (r t'/2)²)

Nüüd lihtsustame seda võrrandit samm-sammult (kirjeldus lühemalt):

1. Jagame mõlemad pooled 2-ga: 1/2 c t' = √(a² + (r t'/2)²)
2. Ruutime mõlemad pooled: (1/4) c² t'² = a² + (r t'/2)²
3. Kirjutame (r t'/2)² = (r² t'²)/4 ning toome t'² ühisele poole: (1/4) c² t'² - (1/4) r² t'² = a²
4. Võtame ühise teguri (1/4) t'²: (1/4) t'² (c² - r²) = a²
5. Seejärel lahendame t' jaoks: t'² = 4 a² / (c² - r²) = (4 a² / c²) · 1/(1 - r²/c²)
6. Võtame ruutjuure ja rõhutame, et t (kella enda mõõdetud aeg ühe tikuga) on t = 2a / c. Seega saab t' väljendada kujul:

t' = t / √(1 - r²/c²)

See on täpselt see, mida relatiivsusteooria ennustab: Maa pealt vaadeldes näib kiirel liikuval kosmoselaeval asuv kell tiksuvat aeglasemalt — ühe tikuga kuluv aeg t' on suurem kui suhtes kella endale kuuluva ajalõigu t. Tegemist on aja dilatatsiooniga, mida iseloomustatakse sageli Lorentzi-faktoriga

γ = 1 / √(1 - r²/c²),

nii et t' = γ t.

Näide

Kui kosmoselaev liigub kiirusega r = 0,5 c, siis r²/c² = 0,25 ja γ = 1 / √(1 - 0,25) = 1 / √0,75 ≈ 1,1547. Kui kella pardal on ühe tikiga mõõdetud aeg t = 1 s (see on ikkagi kella enda järgi mõõdetud aeg), siis Maa pealt vaadeldes kestab see tik 1,1547 s — sellest tuleneb, et liikuv kell tundub aeglasem.

See valguskella mõttekatse demonstreerib selgelt, kuidas invariantsus (valguse kiirus on kõigile sama) ja lihtne geomeetria viivad relatiivse aja dilatatsioonini. Ajalaius ei ole pelgalt mõõtmisviga — see on fundamentaalne omadus aja ja ruumi struktuurist vastavalt erilise relatiivsusteooria seadustele.

Lisalugemiseks ja interaktiivsete simulatsioonide jaoks võite proovida eksperimenteerida erinevate kiirustega: http://www.1728.org/reltivty.htm

Küsimused ja vastused

K: Mis on valguskell?

K: Mis on aja laienemine?

K: Kuidas saame arvutada, kui palju aeglustub aeg kosmoselaeva peal?

Küsimus: Kuidas töötab valguskell?

K: Millist võrrandit vajame selle arvutuse jaoks?

K: Kuidas on Pythagorase teoreem selle arvutusega seotud?

Otsing