Algebra

Algebra (araabia keelest: الجبر, translitereeritud "al-jabr", mis tähendab "purunenud osade taasühinemine") on matemaatika osa (Ameerika Ühendriikides nimetatakse seda sageli matemaatikaks ja Ühendkuningriigis maths või numeracy ). See kasutab muutujaid, et kujutada väärtust, mis ei ole veel teada. Kui kasutatakse võrdusmärki (=), nimetatakse seda võrrandiks. Väga lihtne muutujaid kasutav võrrand on: 2 + 3 = x. Selles näites on x = 5 või võib ka öelda, et "x on võrdne viiega". Seda nimetatakse x-i lahendamiseks.

Lisaks võrranditele on olemas ka ebavõrdsused (väiksem ja suurem kui). Erilist tüüpi võrrandit nimetatakse funktsiooniks. Seda kasutatakse sageli graafikute koostamisel, sest see muudab alati ühe sisendi üheks väljundiks.

Algebrat saab kasutada reaalsete probleemide lahendamiseks, sest algebra reeglid toimivad reaalses elus ja numbreid saab kasutada reaalsete asjade väärtuste kujutamiseks. Füüsika, inseneriteadus ja arvutiprogrammeerimine on valdkonnad, kus algebrat kasutatakse pidevalt. Seda on kasulik teada ka maamõõtmises, ehituses ja äritegevuses, eriti raamatupidamises.

Inimesed, kes tegelevad algebraga, kasutavad arvude ja arvudega tehtavate matemaatiliste operatsioonide reegleid. Kõige lihtsamad on liitmine, lahutamine, korrutamine ja jagamine. Edasijõudnumad operatsioonid hõlmavad eksponente, alustades ruutudest ja ruutjuurtest.

Algebrat kasutati kõigepealt võrrandite ja ebavõrdsuste lahendamiseks. Kaks näidet on lineaarsed võrrandid (sirge võrrand, y=mx+b) ja kvadraatilised võrrandid, mille muutujad on ruudustatud (korrutatud iseendaga, näiteks: 2*2, 3*3 või x*x).

Ajalugu

Algebra varased vormid töötasid välja babüloonlased ja kreeka geomeetrid, nagu Aleksandria Hero. Sõna "algebra" on aga araabia keele sõna Al-Jabr ("valamine") ladinakeelne vorm ja pärineb matemaatikaraamatust Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah ("Essee valamise ja võrrandi arvutamise kohta"), mille kirjutas 9. sajandil pärsia matemaatik Muhammad ibn Mūsā al-Khwārizmī, kes oli Usbekistanis Khwarizmis sündinud moslem. Ta õitses Al-Ma'mouni alluvuses Bagdadis, Iraagis aastatel 813-833 pKr. ja suri umbes 840 pKr. Raamat toodi Euroopasse ja tõlgiti ladina keelde 12. sajandil. Siis anti raamatule nimi "Algebra". (Matemaatiku nime lõpp, al-Khwarizmi, muudeti ladina keeles kergemini hääldatavaks sõnaks ja sellest sai ingliskeelne sõna algorithm).

Näited

Siin on lihtne näide algebraülesande kohta:

Sue'l on 12 kommi ja Annil 24 kommi. Nad otsustavad jagada, nii et neil on sama palju komme. Mitu kommi jääb kummalegi?

Need on sammud, mida saate probleemi lahendamiseks kasutada:

Et saada sama palju komme, peab Ann andma mõned kommid Sue'ile. Olgu x komme, kui palju komme Ann Sue'le annab.
Sue kommid pluss x peavad olema sama suured kui Ann kommid miinus x. See kirjutatakse järgmiselt: 12 + x = 24 - x
Vähendage võrrandi mõlemast küljest 12. See annab: x = 12 - x. (See, mis juhtub ühel pool võrdusmärki, peab juhtuma ka teisel pool, et võrrand oleks endiselt tõene. Nii et antud juhul, kui 12 lahutati mõlemalt poolelt maha, tekkis vahepealne samm 12 + x - 12 = 24 - x - 12. Pärast seda, kui inimene on sellega hakkama saanud, ei kirjutata keskmist sammu üles).
Lisage võrrandi mõlemale poolele x. See annab: 2x = 12
Jagage võrrandi mõlemad pooled 2-ga. See annab x = 6. Vastus on kuus. Kui Ann annab Sue'le 6 kommi, siis on neil sama palju komme.
Selle kontrollimiseks pane 6 tagasi algsesse võrrandisse, kus x oli: 12 + 6 = 24 - 6
See annab 18=18, mis on õige. Neil mõlemal on nüüd 18 kommi.

Harjutusega saab algebrat kasutada, kui seisad silmitsi probleemiga, mida on liiga raske muul viisil lahendada. Sellised probleemid nagu kiirtee ehitamine, mobiiltelefoni konstrueerimine või haiguse ravimise leidmine nõuavad kõik algebrat.

Algebra kirjutamine

Nagu enamikus matemaatika osades, kirjutatakse z lisamine y-le (või y pluss z) kui y + z. z lahutamist y-st (või y miinus z) kirjutatakse kui y - z. y jagamist z-ga (või y üle z: y z {\displaystyle y \over z} ${y \over z}$ ) kirjutatakse kui y ÷ z või y/z. Kõige sagedamini kasutatakse y/z.

Algebras võib y ja z (või y korda z) korrutamist kirjutada neljal viisil: y × z, y * z, y-z või lihtsalt yz. Korrutamise sümbolit "×" tavaliselt ei kasutata, sest see näeb liiga palju välja nagu täht x, mida sageli kasutatakse muutujana. Samuti võib suurema väljendi korrutamisel kasutada sulgusid: y (z+1).

Kui me algebras korrutame arvu ja tähe, kirjutame numbri tähe ette: 5 × y = 5y. Kui arv on 1, siis 1 ei kirjutata, sest 1 korda mis tahes arv on see arv (1 × y = y) ja seega ei ole seda vaja.

Kõrvalmärkusena olgu öeldud, et algebras ei pea kasutama tähti x või y. Muutujad on lihtsalt sümbolid, mis tähendavad mingit tundmatut arvu või väärtust, seega võite kasutada ükskõik millist muutujat. x ja y on siiski kõige levinumad.

Funktsioonid ja graafikud

Algebra oluline osa on funktsioonide uurimine, sest funktsioonid esinevad sageli võrrandites, mida me püüame lahendada. Funktsioon on nagu masin, millesse saab sisestada arvu (või arvud) ja sealt välja saada teatud arvu (või arvud). Funktsioonide kasutamisel võivad graafikud olla võimsad vahendid, mis aitavad meil võrrandite lahendusi uurida.

Graafik on pilt, mis näitab kõiki muutujate väärtusi, mis muudavad võrrandi või ebavõrdsuse tõeseks. Tavaliselt on seda lihtne teha, kui muutujaid on ainult üks või kaks. Graafik on sageli joon ja kui joon ei paindu ega lähe otse üles-alla, saab seda kirjeldada põhivalemiga y = mx + b. Muutuja b on graafiku y-suunaline lõikepunkt (kus joon ristub vertikaalteljega) ja m on joone kalle või järskus. See valem kehtib graafiku koordinaatide kohta, kus iga punkti kohta joonel kirjutatakse (x, y).

Mõnedes matemaatilistes probleemides, nagu näiteks joone võrrand, võib olla rohkem kui üks muutuja (antud juhul x ja y). Punktide leidmiseks sirgel muudetakse ühte muutujat. Muutujat, mida muudetakse, nimetatakse "sõltumatuks" muutujaks. Seejärel tehakse matemaatika, et teha arv. Saadud arvu nimetatakse "sõltuvaks" muutujaks. Enamasti kirjutatakse sõltumatu muutuja x-ks ja sõltuv muutuja y-ks, näiteks y = 3x + 1. See pannakse sageli graafikule, kasutades x-telge (läheb vasakule ja paremale) ja y-telge (läheb üles ja alla). Seda võib kirjutada ka funktsiooni kujul: f(x) = 3x + 1. Nii et selles näites võiksime x-i asemele panna 5 ja saada y = 16. Kui panna x-i jaoks 2, saaks y=7. Ja 0 x-i jaoks saaks y=1. Seega oleks joon, mis läbiks punktid (5,16), (2,7) ja (0,1), nagu on näha paremal oleval graafikul.

Kui x on võimsusega 1, on see sirge. Kui see on ruut või mõni muu potensiaal, siis on see kõver. Kui see kasutab ebavõrdsust (< või > ), siis tavaliselt on osa graafikust varjutatud, kas üleval või allpool joont.

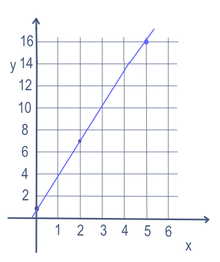
Lineaarne võrrand y=3x+1

Algebra reeglid

Algebras on mõned reeglid, mida saab kasutada võrrandite edasiseks mõistmiseks. Neid nimetatakse algebra reegliteks. Kuigi need reeglid võivad tunduda mõttetud või ilmselged, on mõistlik mõista, et need omadused ei kehti kõigis matemaatika harudes. Seetõttu on kasulik teada, kuidas need aksiomaatilised reeglid on deklareeritud, enne kui neid iseenesestmõistetavaks pidada. Enne reeglite juurde minekut mõelge kahe määratluse üle, mis antakse.

Vastand - {\displaystyle a} vastand on - {\displaystyle -a}.
Reciprocal - pöördväärtus {\displaystyle a} on 1 a {\displaystyle {\frac {1}{a}}} ${\frac {1}{a}}$ .

Reeglid

Liitmise kommutatiivne omadus

"Kommutatiivne" tähendab, et funktsioon annab sama tulemuse, kui arvud vahetada. Teisisõnu, võrrandis olevate terminite järjekord ei ole oluline. Kui kahe termi operaatoriks on liitmine, kehtib "liitmise kommutatiivne omadus". Algebralises mõttes annab see a + b = b + a {\displaystyle a+b=b+a} a+b=b+a .

Pange tähele, et see ei kehti lahutamise puhul! (st a - b ≠ b - a {\displaystyle a-b\neq b-a} $a-b\neq b-a$ )

Korrutamise kommutatiivne omadus

Kui kahe termi operaator on korrutis, kehtib "korrutamise kommutatiivne omadus". Algebralises mõttes annab see a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} $a\cdot b=b\cdot a$ .

Pange tähele, et see ei kehti jagamise puhul! (st a b ≠ b a {\displaystyle {\frac {a}{b}}\neq {\frac {b}{a}}} ${\frac {a}{b}}\neq {\frac {b}{a}}$ , kui a ≠ b {\displaystyle a\neq b} $a\neq b$ ) )

Liitmise assotsiatiivne omadus

"Assotsiatiivne" viitab numbrite rühmitamisele. Liitmise assotsiatiivne omadus tähendab, et kolme või enama termini liitmisel ei ole oluline, kuidas need terminid on grupeeritud. Algebraliselt annab see a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} . Pange tähele, et see ei kehti lahutamise korral, nt 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1=0-(0-1)\neq (0-0)-1=-1} $1=0-(0-1)\neq (0-0)-1=-1$ (vt distributiivne omadus).

Korrutamise assotsiatiivne omadus

Korrutamise assotsiatiivne omadus tähendab, et kolme või enama termi korrutamisel ei ole oluline, kuidas need terminid on grupeeritud. Algebraliselt annab see a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c} $a\cdot (b\cdot c)=(a\cdot b)\cdot c$ . Pange tähele, et see ei kehti jagamise korral, nt 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\displaystyle 2=1/(1/2)\neq (1/1)/2=1/2} $2=1/(1/2)\neq (1/1)/2=1/2$ .

Jaotusväärtuse omadus

Distributiivne omadus väidab, et arvu korrutamist teise terminiga saab jaotada. Näiteks: a ⋅ ( b + c ) = a b + a c {\displaystyle a\cdot (b+c)=ab+ac} $a\cdot (b+c)=ab+ac$ . (Ärge ajage seda segi assotsiatiivsete omadustega! Näiteks a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\displaystyle a\cdot (b+c)\neq (a\cdot b)+c} $a\cdot (b+c)\neq (a\cdot b)+c$ .).

Additiivne identiteedi omadus

Identiteedi all mõistetakse arvu omadust, et see on võrdne iseendaga. Teisisõnu, on olemas kahe arvu operatsioon nii, et see on võrdne summa muutujaga. Additiivne identsuse omadus ütleb, et mis tahes arvu ja 0 summa on see arv: a + 0 = a {\displaystyle a+0=a} a+0=a . See kehtib ka lahutamise puhul: a - 0 = a {\displaystyle a-0=a} a-0=a .

Multiplikatiivne identsuse omadus

Korrutava identiteedi omadus ütleb, et mis tahes arvu ja 1 korrutis on see arv: a ⋅ 1 = a {\displaystyle a\cdot 1=a} $a\cdot 1=a$ . See kehtib ka jagamisel: a 1 = a {\displaystyle {\frac {a}{1}}=a} ${\frac {a}{1}}=a$ .

Additiivne pöördvõrdeline omadus

Additiivne pöördväärtus on mõnevõrra nagu aditiivse identiteedi omaduse vastand. Kui operatsioon on mingi arvu ja selle vastandarvu summa ja see on võrdne 0, siis on see operatsioon kehtiv algebraline operatsioon. Algebraliselt tähendab see järgmist: a - a = 0 {\displaystyle a-a=0} a-a=0 . 1 aditiivne pöördväärtus on (-1).

Multiplikatiivne pöördvõrdeline omadus

Korrutava pöördvõrrandi omadus tähendab, et kui operatsioon on arvu ja selle pöördvõrrandi korrutis ja see on võrdne 1, siis on see operatsioon kehtiv algebraline operatsioon. Algebraliselt tähendab see järgmist: a a = 1 {\displaystyle {\frac {a}{a}}=1} ${\frac {a}{a}}=1$ . Multiplikatiivne pöördväärtus 2 on 1/2.

Täiustatud algebra

Lisaks "elementaaralgebrale" ehk põhialgebrale on olemas kõrgkoolides ja ülikoolides õpetatavad algebra edasijõudnud vormid, nagu abstraktne algebra, lineaaralgebra ja universaalalgebra. See hõlmab ka seda, kuidas kasutada maatriksit paljude lineaarsete võrrandite lahendamiseks korraga. Abstraktne algebra on võrrandites esinevate asjade uurimine, mis ulatub numbritest kaugemale, abstraktsemate arvude rühmadega.

Paljud matemaatikaülesanded on seotud füüsika ja tehnikaga. Paljudes füüsikaülesannetes on muutujaks aeg. Aja puhul kasutatakse tähte t. Algebra põhiideede kasutamine aitab vähendada matemaatilist probleemi kõige lihtsamale vormile, mis teeb raskete probleemide lahendamise lihtsamaks. Energia on e, jõud on f, mass on m, kiirendus on a ja valguse kiirus on mõnikord c. Seda kasutatakse mõnes tuntud võrrandis, nagu f = ma ja e=mc^2 (kuigi selle viimase võrrandi leidmiseks oli vaja keerukamat matemaatikat peale algebra).

Seotud leheküljed

Matemaatika teemade loetelu
Tegevuskord
Parabool
Arvutialgebra süsteem

Küsimused ja vastused

K: Mis on algebra?

V: Algebra on matemaatika osa, mis kasutab muutujaid, et kujutada väärtust, mis ei ole veel teada.

K: Mida tähistab algebras võrdusmärk?

V: Võrdusmärk (=) tähistab algebras võrrandit.

K: Mis on funktsioon algebras?

V: Funktsioon on algebras eriline võrranditüüp, mis muudab alati ühe sisendi üheks väljundiks.

K: Kuidas saab algebrat kasutada reaalsete probleemide lahendamiseks?

V: Algebrat saab kasutada reaalsete probleemide lahendamiseks, sest algebra reeglid toimivad reaalses elus ja numbreid saab kasutada reaalsete asjade väärtuste kujutamiseks. Füüsika, inseneriteadus ja arvutiprogrammeerimine on valdkonnad, kus algebrat kasutatakse pidevalt. Seda on kasulik teada ka maamõõtmises, ehituses ja äritegevuses, eriti raamatupidamises.

K: Milliseid matemaatilisi operatsioone kasutatakse algebras arvudega?

V: Algebras kasutatakse arvude reegleid ja matemaatilisi operatsioone, nagu liitmine, lahutamine, korrutamine ja jagamine arvude peal. Edasijõudnumad operatsioonid hõlmavad eksponente, alustades ruutudest ja ruutjuurtest.

K: Millised on näited algebras kasutatavate võrrandite kohta?

V: Algebras kasutatavate võrrandite näidete hulka kuuluvad lineaarsed võrrandid (sirge võrrand) ja kvadraatilised võrrandid, mille muutujad on ruudustatud (korrutatud iseendaga).