Elementaaralgebra
Algelgebra on kõige elementaarsem algebra vorm, mida õpilastele õpetatakse. See on sageli üks järgmistest matemaatikavaldkondadest, mida õpilastele õpetatakse pärast aritmeetikat. Kui aritmeetikas esinevad ainult arvud ja operaatorid nagu +, -, × ja ÷, siis algebras kasutatakse muutujaid (nagu a, x, y) arvude tähistamiseks. See on kasulik, sest:
- See võimaldab inimestel lahendada probleeme "tundmatute" arvude kohta. See tähendab, et tuleb õppida võrrandeid ja nende lahendamist (näiteks "leia arv x, mille puhul 3 x + 1 = 10 {\displaystyle 3x+1=10}
"). - See võimaldab üldistada reegleid aritmeetikast. Mõned õpilased saavad aru, et 3 + 4 = 4 + 3 {\displaystyle 3+4=4+3}.
, aitab see tõestada, et a + b = b + a {\displaystyle a+b=b+a}
kõigi a ja b jaoks. See teeb algebrast hea sammu abstraktsiooni õppimiseks (üldiste ideede õppimine paljude näidete põhjal). - See aitab inimestel mõista ja luua funktsionaalseid seoseid (mida mõnikord nimetatakse ka põhjuseks ja tagajärjeks). Näide selle kohta on "kui müüakse x piletit, siis on kasum 3 x - 10 {\displaystyle 3x-10}
dollarit".
Need kolm on elementaaralgebra põhisuunad. Elementaaralgebrat kasutatakse sageli paljudes teistes õppeainetes, näiteks loodusteadustes, ärinduses ja ehituses. Abstraktset algebrat, mis on palju edasijõudnum teema, õpetatakse tavaliselt kõrgkoolis hilisemalt.
Lihtsad algebraülesanded
Kui võrrandis on ainult üks tundmatu arv, on seda mõnikord lihtne lahendada. Tundmatut arvu nimetatakse "x":
2 x + 4 = 12. {\displaystyle 2x+4=12.\,} 
Ühe tundmatu summaga lihtsa võrrandi lahendamiseks lisa, lahuta, korruta või jaga võrrandi mõlemad pooled sama arvuga, et panna tundmatu summa x võrrandi ühele poolele. Kui x on ise ühel poolel, kasutage aritmeetikat, et määrata summa võrrandi teisel poolel. Näiteks, lahutades mõlemast küljest 4 ülaltoodud võrrandi mõlemast küljest:
2 x + 4 - 4 = 12 - 4 {\displaystyle 2x+4-4-4=12-4\,} 
saada:
2 x = 8 {\displaystyle 2x=8\,} 
Jagades mõlemad pooled 2ga:
2 x 2 = 8 2 {\displaystyle {\frac {2x}{2}}={\frac {8}{2}}\,} 
saada:
x = 4. {\displaystyle x=4.\,} 
Võib aidata mõelda sellest võrrandist kui kiikrist või tasakaalust, mida teete ühele poole, peate tegema teisele ja teie peamine eesmärk on saada x iseenesest.
Definitsioonid
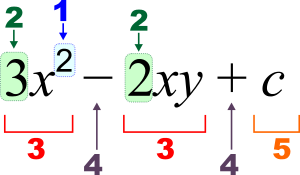
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c}
on järgmised komponendid:
1 : eksponent (võimsus), 2 : koefitsient, 3 : termin, 4 : operaator, 5 : konstant, x , y {\displaystyle x,y} : 
muutujad
Küsimused ja vastused
K: Mis on elementaaralgebra?
V: Elementaaralgebra on kõige elementaarsem algebra vorm, mida õpilastele õpetatakse. Tavaliselt järgneb see aritmeetikale ja hõlmab muutujate (nagu a, x, y) kasutamist arvude tähistamiseks võrrandites.
K: Millised on elementaaralgebra kasutusalad?
V: Elementaaralgebrat saab kasutada tundmatute arvudega seotud probleemide lahendamiseks, aritmeetika reeglite üldistamiseks, funktsionaalsete seoste mõistmiseks ja loomiseks ning seda kasutatakse sageli paljudes teistes õppeainetes, näiteks loodusteadustes, ärinduses ja ehituses.
K: Kuidas aitab elementaaralgebra inimestel mõista abstraktseid ideid?
V: Elementaaralgebra aitab inimestel õppida üldisi ideid paljude näidete põhjal, tõestades, et a+b=b+a kõigi a ja b jaoks. See võimaldab neil paremini mõista abstraktseid mõisteid.
K: Kas abstraktne algebra on edasijõudnum kui elementaaralgebra?
V: Jah, abstraktset algebrat õpetatakse üldiselt kõrgkooli lõpus ja see on palju edasijõudnum kui elementaaralgebra.
K: Milliseid võrrandeid sisaldab elementaaralgebra?
V: Elementaaralgebra hõlmab võrrandeid, mille muutujad (nagu a, x, y) tähistavad numbreid, samuti operaatoreid nagu +,- ,× ja ÷ .
3x+1=10 {\displaystyle 3x+1=10}
K: Kuidas saab elementaaralgebra mõistmine aidata teisi aineid?
V: Elementaaralgebra mõistmine võib aidata teistes õppeainetes, näiteks loodusteadustes, ärinduses või ehituses, sest see võimaldab inimestel lahendada probleeme tundmatute arvude kohta ja luua funktsionaalseid seoseid erinevate muutujate vahel.
