Paralleelipostulaat selgitus ja definitsioon Eukleidese geomeetrias
Geomeetrias on paralleelipostulaat üks eukleidilise geomeetria aksioomidest. Seda nimetatakse sageli ka Eukleidese viiendaks postulaadiks, sest see on Eukleidese elementide viies postulaat. Postulaat on geomeetria alusväide, mida ei tuleta teistest aksioomidest, kuid millel on suuri tagajärgi geomeetriliste konstruktsioonide ja tõestuste jaoks.
Postulaat ütleb, et:
Kui lõikate sirgjoonest kaks joont ja nende kahe sisemise nurga summa on väiksem kui 180°, siis kohtuvad need kaks joont lõpuks, kui neid piisavalt pikaks venitada.
Mis sellest järeldub?
Paralleelipostulaadi olemasolu Eukleidese geomeetrias võimaldab tuletada mitmeid tuntud omadusi ja tunnuseid. Olulisimad järeldused:
- Üksnes üks paralleel: Läbi punkti, mis ei asu antud sirgjoonel, läbib täpselt üks sirgjoon, mis on selle antud sirgjoonega paralleelne. See kuulus ekvivalentne kuju on tuntud ka kui Playfair' aksiom.
- Ristuvad ja vastassuunalised sisemised nurgad: Kui kaks sirget on paralleelsed, siis lõikaja tekitatud vastassuunalised sisemised nurgad on võrdsed; vastupidi, võrdsed sisemised nurgad näitavad paralleelsust.
- Kolmnurga nurkade summa: Eukleidese geomeetrias on kolmnurga sisemiste nurkade summa täpselt 180° (π radianit). Seda saab tuletada paralleelipostulaadist, tõmmates kolmnurga ühe tipu läbi paralleelse rea küljele ja kasutades ristsed ning alternatiivsed nurgad.
Vormid ja ekvivalentsus
Paralleelipostulaadist on mitmeid ekvivalente ja alternatiivseid vormistusi, mis kõik on Eukleidese aksioomide süsteemis omavahel võrdsed. Näited:
- Playfair' aksiom: "Antud joonest väljaspool olevast punktist läbib selle joonega paralleelne joon täpselt üks joon."
- Nurga-summa-vorm: Kui kolmnurga küljele tõmmatud rida tekitab vastavad abinurgad, siis nende omaduste põhjal saab tuletada paralleelsuse ja tagasipöörduda algpostulaadi juurde.
Mitteeukleidilised geomeetriad
Kui paralleelipostulaati ei eeldada või kui seda asendatakse teistsuguse lausega, tekivad muud geomeetria tüübid:
- Hüperboolne (Lobachevski) geomeetria: Läbi antud punkti joone suhtes läheb lõpmata palju jooni, mis ei lõiku antud joonega — st ühtegi "ainult ühte paralleelset" ei ole.
- Elliptiline (sfääriline) geomeetria: Paralleelseid jooni ei eksisteeri — kõik suure ringi suurjooned lõikuvad.
Need mitteeukleidilised geomeetriad näitasid 19. sajandil, et paralleelipostulaadi asendumine erineva postulaadiga viib loogiliselt järjepidevatesse, kuid Eukleidese omadustest erinevatesse geomeetriatesse.
Ajalooline märkus
Eucliduse ajast alates on matemaatikud püüdnud viiendat postulaati teiste aksioomidest tuletada, kuna see tundus vähem ilmne kui teised. Püüdlused (nt Saccheri, Lambert) viisid lõpuks 19. sajandi avastusteni, et selle postulaadi asendamine teisega annab järjepidevad, kuid Eukleidest erinevad geomeetriad. Sellest kujunes oluline samm matemaatilise mõtlemise ja abstraktsuse arengus.
Kasutus ja tähendus
Paralleelipostulaat on praktiliselt kõigi tavapäraste eukleideliku geomeetria tulemuste alus — ehitustöödes, arhitektuuris, karteerimises ja paljudes inseneri- ning füüsikarakendustes, kus ruum ja tavalised tasapinnalised mõõtmised järgivad Eukleidese reegleid. Mõiste mõistmine aitab eristada, millises geomeetrilises mudelis mingi väide kehtib ning millal tuleb arvestada mitteeukleidiliste omadustega.
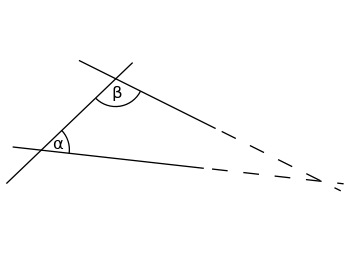
Kui sisemiste nurkade α (alfa) ja β (beeta) summa on väiksem kui 180°, lõikuvad need kaks sirget kuskil, kui mõlemad on pikendatud lõpmatuseni.
Ajalugu
Mõned matemaatikud arvasid, et Eukleidese viies postulaat oli palju pikem ja keerulisem kui ülejäänud neli postulaati. Paljud neist arvasid, et seda saab tõestada teiste lihtsamate aksioomide põhjal. Mõned matemaatikud teatasid, et nad on selle lause tõestanud lihtsamate postulaatide põhjal, kuid kõik nad osutusid ekslikuks.
Playfairi aksioom
Teine uuem lause, mida tuntakse Playfairi aksioomina, on sarnane Eukleidese viienda postulaadiga. See ütleb, et:
Arvestades sirget ja punkti, mis ei asu sellel sirgel, saab läbi selle punkti tõmmata ainult ühe sirge, mis ei kohtuks teise sirgega.
Tegelikult leidsid matemaatikud, et see aksioom ei ole mitte ainult sarnane Eukleidese viienda postulaadiga, vaid sellel on täpselt samad tagajärjed. Matemaatiliselt nimetatakse neid kahte lauset "ekvivalentseteks" lauseteks. Tänapäeval kasutavad matemaatikud Playfairi aksioomi sagedamini kui Eukleidese algset paralleelpostulaati.
Mitte-eukleidiline geomeetria
Lõpuks püüdsid mõned matemaatikud ehitada uusi geomeetriat ilma aksioomi kasutamata. Üks mitte-eukleidilise geomeetria liik on nn elliptiline geomeetria. Elliptilises geomeetrias on paralleelipostulaat asendatud aksioomiga, mis ütleb, et:
Kui on antud sirge ja punkt, mis ei asu sellel sirgel, siis ei saa läbi selle punkti joonistada sirget, mis ei ristu lõpuks teise sirgega.
Matemaatikud leidsid, et kui nad asendasid Eukleidese viienda postulaadi selle aksioomiga, suutsid nad siiski tõestada paljusid teisi Eukleidese teoreeme. Üks võimalus kujutleda elliptilist geomeetriat on mõelda maakera pinnale. Gloobusel näivad geograafilised jooned olevat ekvaatoril paralleelsed, kuid kõik need kohtuvad poolustel. sajandi lõpus näidati, et elliptiline geomeetria on järjepidev. See tõestas, et Eukleidese viies postulaat ei ole sõltumatu teistest postulaatidest. Pärast seda lõpetasid matemaatikud enamasti katsed tõestada viiendat postulaati teiste nelja postulaadi põhjal. Selle asemel hakkasid paljud matemaatikud uurima teisi geomeetriaid, mis ei järgi Eukleidese viiendat postulaati.
Teine aksioom, millega matemaatikud mõnikord asendavad Eukleidese viienda aksioomi, ütleb, et:
Kui on antud sirge ja punkt, mis ei asu sellel sirgel, siis saab läbi selle punkti joonistada vähemalt kaks sirget, mis ei ristu lõpuks teise sirgega.
Seda nimetatakse hüperbooliliseks geomeetriaks.
Teine geomeetria lihtsalt eemaldab Eukleidese viienda postulaadi ja ei asenda seda millegi muuga. Seda nimetatakse neutraalseks geomeetriaks või absoluutseks geomeetriaks.
