Laviiniefekt krüptograafias: definitsioon, tähtsus plokkšifrites ja hashides
Laviiniefekt krüptograafias: kuidas väikesed sisendi muutused tekitavad suuri väljundi muutusi — tähtsus plokkšifrites ja hash-funktsioonides ning turvalisuse alused.
Laviiniefekt ("maalihkeefekt") on plokkšifrite ja krüptograafiliste hash-funktsioonide algoritmide omadus. Seda soovitakse sageli krüptograafias. See efekt tähendab, et väljund peab muutuma oluliselt, isegi kui sisend muutub vaid vähe. Heade plokkšifrite puhul tähendab see tavaliselt järgmist: väike muutus võtmes või lihtkirjas peaks põhjustama tugeva ja näiliselt juhusliku muutuse salakirjas. Laviiniefekti tugevus aitab tagada, et ründajal ei ole võimalik lihtsate statistiliste meetoditega sisendit tuvastada või ennustada.
Mida laviiniefekt täpsemalt tähendab
Praktiliselt mõõdetakse laviiniefekti sageli nii, et ühe sisendbiti muutmine põhjustab ligikaudu 50% bittide muutumise tõenäosust väljundis. See omadus on eriti oluline nii plokkšifrite kui ka hash-funktsioonide jaoks, kuna see tagab suure difusiooni: väikesed muutused sisendis "levivad" kiiresti kogu väljundisse. Kui algoritm kasutab iteratsioone, siis need muutused kumuleeruvad ja iga bit väljundis sõltub lõpuks paljudest või kõigist bittidest sisendist.
Ajalooline ja teoreetiline taust
Terminit laviiniefekt kasutas esmakordselt Horst Feistel (Feistel 1973). Konseptsioon on seotud Claude Shannoni idee‑ga, mida kirjeldatakse sageli kui segaduse (confusion) ja difusiooni (diffusion) omadusi krüptosüsteemides. Matemaatiliselt ja fenomenoloogiliselt on laviiniefekti kirjeldamisel abiks ka liblikaefekti mõiste, mis rõhutab väikesest muutusest algavat suurenevat mõju.
Olulisus plokkšifrites
Plokkšifrite disainimisel on laviiniefekt üks peamisi eesmärke. Selle saavutamiseks kasutatakse tavaliselt mitmeid komponente ja põhimõtteid:
- mitmekordsed iteratsioonid (ringid), et väiksest muutusest saaks aeglaselt globaalne mõju;
- mitte-lineaarsed asendustabelid (S-boxid) ja permuteerimiskihid, mis tagavad segaduse ja difusiooni;
- hästi kavandatud difusioonikihid (näiteks lineaarne transformatsioon), mis "lahjendavad" ühe bitti mõju üle palju väljundbitte.
Seetõttu on enamik plokkšifreid tootesifreid (product ciphers), mis kombineerivad asendusi ja permutatsioone. Tugev laviiniefekt vähendab oluliselt võimalusi kasutada differentsiaalanalüüsi või lineaaranalüüsi efektiivselt.
Olulisus krüptograafilistes hash‑funktsioonides
Hash‑funktsioonide puhul aitab laviiniefekt tagada, et väikseimgi muudatus sisendis (nt üks bitt või üks tähemärk) muudab seluruh digesti fundamentaalselt. See on oluline omadus nii juhuslikkuse sarnase väljundi kui ka põhiliste turvakriteeriumide — nagu tahkestus (preimage resistance), teise astme tahkestus (second‑preimage resistance) ja kokkupõrkekindlus — säilitamiseks. Hashi konstruktsioonides (nt Merkle–Damgård või SPN‑stiilis kompressioonifunktsioonid) kasutatakse suuri andmeplokke ning tugev difusioonikiht aitab saavutada kiiresti laviiniefekti kogu häšis.
Kuidas laviiniefekti mõõdetakse ja testitakse
Levinud lähenemisviisid ja testid hõlmavad:
- aiavälja (avalanche) test: flipping ühe sisendbiti ja mõõtes, kui paljud väljundbitid muutuvad; ideaalne on ~50%;
- Striktne laviinikriteerium (Strict Avalanche Criterion, SAC): iga üksik sisendbitti muutus peaks muutma iga väljundbitti sõltumatult tõenäosusega 1/2;
- Bit Independence Criterion (BIC): väljundbittide muutumised peaksid olema omavahel võimalikult sõltumatud, kui muuta üks sisendbitt;
- statistilised testid (nt NIST testipakett, chi‑ruut, korrelatsioonianalüüs jne) suure hulga juhuslike sisendite ja ühebitiliste muutuste korral.
Järeldused disaini ja rünnaku seisukohalt
Kui plokkšifreering või krüptograafiline hash-funktsioon ei vasta olulineul määral laviiniefektile, siis on selle juhuslikkus halb ja algoritm võib olla haavatav. Sellisel juhul võib kriptoanalüütik teha prognoose sisendi kohta, kui talle antakse ainult väljund. See võib viia algoritmi osalise või täieliku murdmiseni. Seetõttu on disaineritel huvi ehitada sisse mitte ainult kõrge laviiniefekti, vaid ka tugev mitte-lineaarsus, piisav arv ringe ja hea difusioonikiht.
Praktilised näited ja mõtteainet
Mõned kaasaegsed algoritmid (näiteks AES plokkšifiir ja populaarseid hash‑peresid nagu SHA‑2 ja SHA‑3 perekonnad) on kavandatud nii, et saavutada relativselt kiire laviiniefekt juba mõne ringi järel. Vanemad algoritmid, mille laviiniefekt ei olnud piisav või mille komponendid avaldasid statistilisi ebaühtlusi, on viinud edukate krüptoanalüüside ja murdmisteni.
Lõpetuseks: laviiniefekt ei ole ainus turvakriteerium, kuid see on keskne omadus, mida tuleb hinnata nii disainis kui ka hindamises. Hea laviiniefekt koos tugevate matemaatiliste filtrite ja põhjalike statistiliste testidega aitab tagada, et krüptosüsteemid on vastupidavamad reaalsetele rünnakutele.
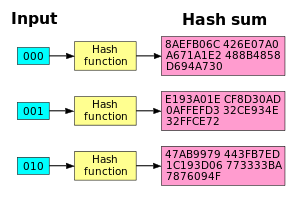
SHA1 hash-funktsioonil on hea laviiniefekt. Kui üks bitt muutub, muutub hash-summa täiesti erinevaks.
Nimi
Nime päritolu on maalihked. Väike kivi võib maha kukkuda, minna koos lumega ja teha hävitava maalihke. Kivi oli väike, kuid võis põhjustada palju hävingut. See on sama, mida see mõju teeb. Väike muutus sisendis (kivi) peaks muutma väljundit (maastik).
Range laviinikriteerium
Strict Avalanche Criterion (SAC; "tugeva maalihke kriteerium") on bool'i funktsioonide omadus. See on oluline krüptograafias. See on täidetud, kui kõik väljundbitid muutuvad 50 % tõenäosusega, kui üks sisendbit muutub.
SAC põhines evolutsiooni täielikkuse ja laviini mõistetel. Selle võtsid kasutusele Webster ja Tavares 1985. aastal. Tänapäeval on see nõue iga kaasaegse krüptograafilise süsteemi jaoks. Seda täitsid näiteks kõik AES-võistluse finalistid.
Biti sõltumatuse kriteerium
Biti sõltumatuse kriteerium (BIC; bitist sõltumatu kriteerium) on kriteerium. See läheb: Kui üks sisendbit muudetakse (inverteeritakse), peaksid kaks väljundbitti muutuma üksteisest sõltumatult. See kehtib kõigi bittide kohta.
See ei oleks näiteks rahuldatud, kui üks väljundbit muutub ainult siis, kui ka teine väljundbit muutub. Nad võivad muutuda ainult seetõttu, et sisendbit muutus. Vastasel juhul sõltuksid väljundbitid üksteisest.
Seotud leheküljed
- Segadus ja levik
Küsimused ja vastused
K: Mis on laviiniefekt?
V: Laviiniefekt (tuntud ka kui "maalihkeefekt") on plokkšifrite ja krüptograafiliste hash-funktsioonide algoritmide omadus, mis väidab, et väike muutus võtmes või lihtkirjas peaks põhjustama tugeva muutuse krüptetekstis.
K: Kes kasutas esimesena mõistet "laviini efekt"?
V: Terminit "laviiniefekt" kasutas esimest korda Horst Feistel 1973. aastal.
K: Kuidas on see seotud Shannoni segaduse omadusega?
V: Laviiniefekti mõiste tuvastati Shannoni segaduse omadusega, mis väidab, et kui plokkšifreering või krüptograafiline hash-funktsioon ei vasta sellele olulisel määral, siis on see halvasti juhuslik ja seda saab osaliselt või täielikult murda (crackida).
K: Millised on mõned projekteerimiseesmärgid tugevate salakirjade loomisel?
V: Tugevaid šifreid luues püütakse neisse sisse ehitada hea laviiniefekt, kasutades matemaatilisi põhimõtteid, näiteks liblikatefekti. Seetõttu on enamik plokkšifreid tootesifreid ja miks hash-funktsioonidel on suured andmeplokid.
K: Mis juhtub, kui algoritm ei vasta laviiniefektile?
V: Kui algoritm ei vasta olulisel määral laviiniefektile, siis on selle juhuslikkus halb ja seda võivad osaliselt või täielikult murda (murda) krüptoanalüütikud, kes suudavad teha prognoose sisendi kohta ainult antud väljundi põhjal.
K: Miks kasutatakse enamikus plokkšifrites tootesifreid?
V: Enamik plokkšifreid kasutab tooteküptomeetreid, sest nende abil saab neisse sisse ehitada hea avanzi efekti, kasutades matemaatilisi põhimõtteid, nagu näiteks liblikaefekt.
K: Miks on hash-funktsioonidel suured andmeplokid?
V: Hash-funktsioonidel on suured andmeplokid, sest see aitab matemaatiliste põhimõtete (nt liblikate efekt) abil saavutada head avalance-efekti.
Otsige