Tõenäosusruum: definitsioon, komponendid ja Kolmogorovi aksioomid
Tõenäosusruum: selge definitsioon, näidisruum, sündmused, σ-algebra ja tõenäosusmõõt – Kolmogorovi aksioomid ja praktilised näited matemaatiliseks mõistmiseks.
Tõenäosusruum on matemaatiline mudel, mida kasutatakse teaduslike katsete ja juhuslike protsesside kirjeldamiseks. Tõenäosusruum annab formaalse raamistikku, mille kaudu määratletakse võimalikud tulemused, huvipakkuvad sündmused ning nende esinemise tõenäosused. Tõenäosusruum koosneb kolmest põhikomponendist:
- Näidisruum (sample space) – tähistatakse sageli sümboliga Ω. Näidisruumis on loetletud kõik võimalikud ühe katse või eksperimendi tulemused (nt mündi viskamisel Ω = {“Kruup” , “Küür”} või täringu viskamisel Ω = {1,2,3,4,5,6}).
- Sündmuste kogum – tavaliselt mitteametlikult nimetatud sündmuseks on mingi näidisruumi alamkogu (nt “saab paarisarvu”). Kõigi huvipakkuvate alamhulkade kogumit, millele võib määrata tõenäosuse, nimetatakse σ-algebraks (sigma-algebra) ja tähistatakse F {\displaystyle \scriptstyle {\mathcal {F}}}.
Sigma-algebra on sulgunud komplemendi ja loendatavate ühinemiste suhtes, mis tagab loogiliselt sidusa sündmuste süsteemi. - Funktsioon – tõenäosusmõõt (tähistatakse tavaliselt tähega P), mis määrab igale sigma-algebra elemendile ehk sündmusele reaalarvu vahemikus [0,1], mida tõlgendatakse selle sündmuse tõenäosusena.
Mis on sündmus ja kuidas see "aset leiab"?
Tulemus (või elementaarne tulemus) on mudeli ühekordse täitmise konkreetne väljund, tähistatuna tavaliselt ω ∈ Ω. Kuna üksikutest elementaarsetest tulemustest on sageli vähe informatiivset, käsitletakse huvipakkuvate olukordade kirjeldamiseks nende rühmi ehk sündmusi (alamahulkasid). Kõikide selliste sündmuste kogum on σ-algebra F {\displaystyle \scriptstyle {\mathcal {F}}}. Kui looduse (või juhuse) poolt valitakse näidisruumist üks tulemus ω, siis kõik sündmused, mis kuuluvad F-s, ja mis sisaldavad seda tulemust, loetakse aset leidnuteks (st sündmus "juhtus").
Tõenäosusmõõt ja Kolmogorovi aksioomid
Tõenäosusruumi täielikuks määratlemiseks vajame funktsiooni P, mis määrab igale sündmusele tõenäosuse. Aksioomaatilise lähenemise autoriks on tuntud matemaatik Andrei Kolmogorov, kes 1930. aastatel sõnastas kolm põhialust (aksioomi), mida iga tõenäosusmõõt peab rahuldama:
- Mittetühisuse ja mitte-negatiivsuse aksioom: iga sündmuse A korral P(A) ≥ 0.
- Ühikule vastavus: P(Ω) = 1 — ehk kogu näidisruumi toimumise tõenäosus on 1.
- Loendatav additiivsus (kõrgemate sündmuste eraldatuse korral): kui A1, A2, A3, ... on paarikaupa disjunktsete sündmuste jada (st Ai ∩ Aj = ∅, kui i ≠ j), siis P(⋃_{i=1}^∞ Ai) = Σ_{i=1}^∞ P(Ai).
Need aksioomid on lihtsad, ent äärmiselt võimsad: neist järgnevad mitmed kasutatavad omadused, näiteks
- P(∅) = 0 (põletava jõuga tühi sündmus ei saa juhtuda),
- monotoonsus: kui A ⊂ B, siis P(A) ≤ P(B),
- lühike additiivsus: kui A ja B on disjunktsed, siis P(A ∪ B) = P(A) + P(B),
- kõige üldisemalt: loendatav additiivsus võimaldab käsitleda nii lõplikke kui ka loendamatuid ühinemisi.
Tõlgendused ja näited
Kolmogorovi axioomid annavad formaalse raamistiku mitmele tõlgendusele:
- Sageduslik tõlgendus: kui eksperimenti korrata väga paljud kordsed ja loogiliselt identsed katsed, siis sündmuse suhteline esinemissagedus läheneb P(A) väärtusele.
- Subjektiivne (bayesia) tõlgendus: P(A) võib väljendada isiklikku veendumust või teadmistebaasil põhinevat hindeid sündmuse toimumise kohta.
Lihtsad näited:
- Ühe mündi viskamine: Ω = {Kruup, Küünar}, tavaliselt P({Kruup}) = P({Küünar}) = 1/2 (kui münt on õiglane).
- Täisarvu täringu viskamine: Ω = {1,2,3,4,5,6}, iga tulemuse tõenäosus 1/6 eeldusel, et täring on ehe.
- Jätkuv juhuslik suurus (nt normaaljaotus): sündmused määratakse mõõtmete kaudu ja tõenäosus määratakse tiheduse integreerimise abil; üksikpunkti tõenäosus võib olla 0, ent intervalli tõenäosus on integraal selle tiheduse üle.
Kokkuvõte
Tõenäosusruum (Ω, F {\displaystyle \scriptstyle {\mathcal {F}}}. , P) annab rangelt defineeritud aluse tõenäosuste arvutamiseks: näidisruum koos sündmuste kogumiga (σ-algebra) ja tõenäosusmõõduga. Kolmogorovi aksioomid tagavad selle, et tõenäosuste käitumine on intuitiivselt mõistetav ja matemaatiliselt järjekindel, võimaldades rakendusi nii statistikas, inseneriteadustes, füüsikas kui ka paljudes teistes valdkondades.
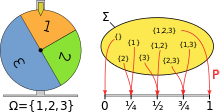
Õnneratta modelleerimine tõenäosusruumi abil
Küsimused ja vastused
K: Mis on tõenäosusruum?
A: Tõenäosusruum on matemaatiline mudel, mida kasutatakse teaduslike katsete kirjeldamiseks. See koosneb kolmest osast: valikuruum, mis loetleb kõik võimalikud tulemused, sündmuste kogum, mis seostab nulli või rohkem tulemusi, ja funktsioon, mis määrab igale sündmusele tõenäosused.
K: Millest koosneb valikuruum?
V: Valimisruum koosneb kõigist võimalikest tulemustest, mis sageli kirjutatakse kujul Ω {\displaystyle \Omega }. ja tulemus kui ω {\displaystyle \omega }. .
K: Mis on tulemus?
V: Tulemus on mudeli ühe täitmise tulemus.
K: Milleks kasutatakse tõenäosusruumides sündmusi?
V: Sündmusi kasutatakse tulemuste rühmade iseloomustamiseks, kuna üksikutest tulemustest võib olla vähe kasu. Kõigi selliste sündmuste kogumit nimetatakse σ-algebraks, mida mõnikord kirjutatakse kui F {\displaystyle {\mathcal {F}}} .
K: Kuidas määratakse igale sündmusele tõenäosused?
V: Tõenäosused määratakse igale sündmusele tõenäosusmõõdufunktsiooni P abil.
K: Kes võttis kasutusele tõenäosusruumi mõiste? V: 1930. aastatel võttis tuntud nõukogude matemaatik Andrei Kolmogorov koos teiste tõenäosuse aksioomidega kasutusele tõenäosusruumide mõiste.
Otsige