Märk matemaatikas — positiivne, negatiivne ja nulli tähendus

Avasta märgi roll matemaatikas: kuidas positiivne, negatiivne ja null mõjutavad arve, operatsioone ja tähendust — selge ülevaade ja praktilised näited.

Autor: Leandro Alegsa

15-10-2025

Matemaatikas viitab sõna "märk" omadusele olla positiivne või negatiivne. Iga reaalarv (mis ei ole null) on kas positiivne või negatiivne ja seega on tal märk. Null ise on ilma märgita ehk märkideta. Lisaks märkide panemisele reaalarvudele kasutatakse sõna märk kogu matemaatikas matemaatiliste objektide positiivsust ja negatiivsust tähendavate osade tähistamiseks. Tavaliselt, kui numbreid nähakse ilma märgita, peetakse neid positiivseks arvuks.

Sõna märk kasutatakse mõnikord ka erinevate matemaatiliste märkide, näiteks pluss- ja miinusmärgi ning korrutustähe tähistamiseks.

Alljärgnevalt on põhjalikum selgitus märgi tähendusest ja olulisematest reeglitest, mis aitavad mõista, kuidas märk mõjutab arvutusi ja omadusi.

Põhilised mõisted

Positiivne arv — arv suurem kui 0; näiteks +3 (tihti kirjutatakse lihtsalt 3).
Negatiivne arv — arv väiksem kui 0; näiteks −5.
Null — arv 0 on erand: tal ei ole positiivset ega negatiivset märki.
Suhteline märgis — märk on omadus, mis eristab positiivset ja negatiivset osa ning mõjutab aritmeetilisi tulemusi.

Reeglid põhitehete kohta

Liitmine ja lahutamine: tulemuse märk sõltub summandite suurustest ja märkidest. Näiteks 5 + (−3) = 2, aga (−5) + 3 = −2. Lahutamine a − b saab käsitleda kui liitmist a + (−b).
Korrutamine: kaks võrdse märgiga arvu annavad positiivse tulemuse, erineva märgiga arvu korrutamisel on tulemus negatiivne. Näited: (−2)·(−3)=6, (−2)·3=−6.
Jagamine: jagamise märgi reeglid järgnevad korrutamisele — jagades kaks sama märki omavat arvu, on tulemus positiivne; erinevate märkidega jagamisel on tulemus negatiivne. Jagamisel nulliga tuleb olla ettevaatlik: jagamine nulliga pole määratletud.
Kordne null: kui mingi tehe sisaldab tegurit 0 (korrutamisel), on tulemuseks 0 — see kehtib sõltumata teiste tegurite märkidest.

Märgi ja absoluutväärtuse seos

Absoluutväärtus |x| näitab arvu kaugust nullist ilma märgita. Näiteks |3| = 3 ja |−3| = 3. Absoluutväärtus annab informatsiooni suuruse kohta, märgi teave ütleb, millises suunas (positiivne või negatiivne) arv paikneb.

Märgi funktsioon

Matemaatikas kasutatakse tihti märgi funktsiooni sgn(x), mis annab kiire ülevaate arvu märgist:

sgn(x) = 1, kui x > 0
sgn(x) = 0, kui x = 0
sgn(x) = −1, kui x < 0

See funktsioon on kasulik numbrite jagamiseks kategooriatesse positiivne/negatiivne/zero ja analüüsimisel, kus huvi on vaid märgil.

Märk muudes kontekstides

Sõna "märk" kasutatakse ka funktsiooni käitumise kirjeldamiseks: öeldakse, et funktsioon on mingil vahemikul positiivne või negatiivne (näiteks f(x) > 0 või f(x) < 0). See on oluline juur- ja nullkohtade analüüsis.
Mõnes valdkonnas on "märk" teine tähendus, näiteks permutatsiooni märk (parity), mis ütleb, kas permutatsiooni saab sõelumult paaritu või paaritu arvu elementide vahetustega — see on teistsugune mõiste kui positiivne/negatiivne
Komplekssed arvud ei ole üldiselt järjestatavad — neil ei ole positiivset või negatiivset märki nagu reaalarvudel; sellepärast räägitakse kompleksarvude puhul pigem reaalsest ja imaginaarsest osast ning modulist (absoluutväärtusest).

Märkide kirjutamise ja tähistamise tavapraktika

Kui arvukirjas ei ole plussmärki, loetakse arv tavaliselt positiivseks (nt 7 tähendab +7).
Pluss- ja miinusmärki kasutatakse ka väljendites ning esitustes selgitamaks termide rolle (näiteks +x, −x).
Märgi käsitlemisel on kasulik mõista, et tehete ümberkujundused (nt lahutamine liitmise kaudu) võimaldavad selgemalt jälgida, kuidas märk lõpptulemust mõjutab.

Kokkuvõtteks: märk on lihtne, ent fundamentaalne omadus, mis eristab reaalarvude positiivseid ja negatiivseid elemente ning mõjutab kõiki aritmeetilisi operatsioone. Null on eriline — tal puudub märk. Lisaks arvudele kasutatakse mõistet "märk" ka laiemalt matemaatikas, kuid tähendus sõltub kontekstist.

Pluss- ja miinussümboleid kasutatakse numbri märgi näitamiseks. Pluss tähendab positiivset ja miinus negatiivset.

Numbri märk

Reaalarv on positiivne, kui see on suurem kui null, ja negatiivne, kui see on väiksem kui null. Seda omadust, kas arv on positiivne või negatiivne, nimetatakse arvu märgiks. Nullile endale ei omistata märki.

Aritmeetikas tähistatakse numbri ees sageli pluss- või miinusmärki. Näiteks +3 tähistab positiivset arvu 3 ja -3 tähistab negatiivset arvu 3. Kui pluss- või miinusmärki ei ole antud, on peamine viis näha, et arv on positiivne.

Mis tahes arvu, mis ei ole null, märgi saab muuta positiivseks, kasutades absoluutväärtuse funktsiooni. Näiteks on absoluutväärtus -3 ja absoluutväärtus 3 mõlemad võrdsed 3. Sümbolites kirjutatakse see |-3| = 3 ja |3| = 3.

Nulli märk

Number null ei ole ei positiivne ega negatiivne ja seetõttu ei ole tal mingit märki. Aritmeetikas tähendavad nii +0 kui ka -0 sama arvu 0.

Tähendused märgid

Kuna null ei ole ei positiivne ega negatiivne, kasutatakse mõnikord tundmatu arvu märgi tähistamiseks järgmisi mõisteid:

Arv on positiivne, kui see on suurem kui null.
Arv on negatiivne, kui see on väiksem kui null.
Arv on mittenegatiivne, kui see on suurem või võrdne nulliga.
Arv on mittepositiivne, kui see on väiksem või võrdne nulliga.

Seega on mittenegatiivne arv kas positiivne või null, samas kui mittenegatiivne arv on kas negatiivne või null. Näiteks reaalarvu absoluutväärtus on alati mittenegatiivne, kuid mitte tingimata positiivne.

Sama määratlust kasutatakse mõnikord funktsioonide puhul, mis võtavad reaal- või täisarvuväärtusi. Näiteks nimetatakse funktsiooni positiivseks, kui kõik selle väärtused on positiivsed, või mittenegatiivseks, kui kõik selle väärtused on mittenegatiivsed.

Nurga märk

Paljudes tekstides on tavaline, et märk on koos nurga, eriti asetseva nurga või pöördenurga mõõtmega. Sellises olukorras ütleb märk, kas nurk on päripäeva või vastupäeva. Kuigi võib kasutada erinevaid konventsioone, on matemaatikas tavaline, et vastupäeva nurgad loetakse positiivseks ja päripäeva nurgad loetakse negatiivseks.

Samuti on võimalik kolmemõõtmelisele pöördenurgale märki panna, eeldades, et pöörlemistelg on orienteeritud. Konkreetselt loetakse parempoolne pöörlemine ümber telje tavaliselt positiivseks, vasakpoolne pöörlemine aga negatiivseks.

Suunamärk

Aritmeetikas ja füüsikas on tavaline, et teatud suundasid nimetatakse positiivseks või negatiivseks. Näiteks joonistatakse arvjoon tavaliselt nii, et positiivsed arvud on paremal ja negatiivsed arvud vasakul:

Kartesiaanlikul tasapinnal peetakse tavaliselt paremale ja ülespoole suunatud suunda positiivseks, kusjuures paremale suunatud on positiivne x-suund ja ülespoole suunatud on positiivne y-suund.

Muud tähendused

Lisaks reaalarvu märgile kasutatakse sõna märk ka mitmel seotud viisil kogu matemaatikas ja loodusteadustes:

Graafiteoorias on märgistatud graaf, mille iga serv on tähistatud positiivse või negatiivse märgiga.
Füüsikas on igal elektrilaengul oma märk, kas positiivne või negatiivne. Üldiste reeglite kohaselt on positiivne laeng prootoniga sama märgiga laeng ja negatiivne laeng on elektroniga sama märgiga laeng.

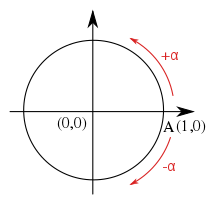
x-teljest mõõtes loetakse nurgad ühikuringil positiivseks vastupäeva ja negatiivseks päripäeva suunas.

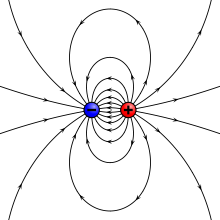
Elektrilaeng võib olla positiivne või negatiivne.