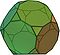
Arhimedese hulktahukad: definitsioon, tüübid ja põhiomadused

Geomeetrias on Arhimedese hulktahukas (Archimedean solid) kumer tahukas, mis koosneb hulknurkadest. Tegemist on erilise tüüpi korrapäraste tahukate kogumiga: iga tahk on korrapärane hulknurk, kuid tahkude tüüpide arv võib olla suurem kui üks. Arhimedese hulktahukad on ühtlasi näide sellistest kujunditest, millel on suur sümmeetria nii, et kõik tipud on üksteisega võrreldavad (sama tipukonfiguratsioon).

Iga nägu on korrapärane hulknurk (st kõik selle külgede ja nurkade omadused on võrdsed).
Kõigil tipupunktidel ehk nurgadel on sama ümbrus: tipu juures kokku tulevate tahkude tüübid ja järjekord on omavahel võrdsed (tähistatakse sageli tipukonfiguratsioonina, nt 3.4.3.4 jne).
See kuju ei ole ei platooniline tahkis, prisma ega antiprisma — st need ei kuulu regulaarsete Platonilike tahukate hulka ning neid ei loeta tavaliselt prisma- ega antiprisma-klassi kuuluvateks kujunditeks.

Arhimedese hulktahukaid loetakse kas 13-ks või 15-ks sõltuvalt loendamisreeglist: kui peetakse peegelpildid kongruentseteks, on neid 13; kui aga kaheksa jahtusid käsitletakse eraldi (st vasak- ja parempoolseid keerulisemaid vorme eraldi), on neid 15. Neist kahest kujundist on kaks varianti, mida ei saa pööramise abil kongruentseks muuta — need kujundid on chiralsed ehk esinevad vasaku- ja parempoolse (peegelpildi) vormina (näidetena tavaliselt nimetatakse neid "snub cube" ja "snub dodecahedron").

Arhimedese hulktahukate klassifikaatorid eristavad neid järgmiselt: kõik tahud on korrapärased hulknurgad ja iga tipu juures olevate tahkude järjekord on kõigil tippudel sama. Need omadused teevad need "ühtlasteks" (uniforms) polüeedriteks — täpsemalt on Archimedean solids kõik konvekssed uniformsed polüeedrid, välja arvatud Platonilised tahukad, prismaatilised ja antiprismaatilised variandid.

Konkreetsed näited Archimedese hulktahukatest hõlmavad (nimed inglise keeles/tavaliselt kasutatavad nimetused): truncated tetrahedron (lõigatud tetraaeeder), truncated cube (lõigatud kuup), truncated octahedron, truncated dodecahedron, truncated icosahedron, cuboctahedron, icosidodecahedron, rhombicuboctahedron, rhombicosidodecahedron, truncated cuboctahedron, truncated icosidodecahedron ning snub cube ja snub dodecahedron (keerulised ehk chiralsed vormid). Igal neist on kindel arv nägusid, servi ja tippe, mis vastavad Eulerile omasele seosele V − E + F = 2 konveksses polüeedris.

Arhimedese tüüpi hulktahukate konstrueerimine toimub sageli Platoniliste tahukate geomeetriliste operaatorite abil: kärpimine (truncation), kaheks jagamine, rannikute lisamine (cantellation), snubbing (keeramine) jms. Need operatsioonid muudavad algset regulaarset tahukate kombinatsiooni nii, et saadakse mitu tüüpi korrapäraseid polügoone nägudena, samal ajal säilitades tipuühtsuse.

Vana-Kreeka matemaatiku Archimedese järgi, kellele need kujundid traditsiooniliselt omistatakse, on need vormid tõenäoliselt tuntud juba 3. sajandil eKr. Archimedese originaalkirjutised on kadunud, kuid 4. sajandil kokkuvõtte tegi Pappus Aleksandriast, kes säilitas osalise informatsiooni. Renessansi ajal hindasid kunstnikud ja matemaatikud puhtaid vorme ja avastasid need kujundid uuesti; Johannes Kepler jõudis umbes 17. sajandi alguses selliste kujundite loendile ja uurimise süvendamisele, mistõttu nende ajalooline uurimus kulges osaliselt renessansiaegse geomeetria ja kunstiga paralleelselt.

Arhimedese hulktahukate dualid (kahepoolsed polüeedrid) kuuluvad Catalan'i tahukate rühma — nende näod ei ole enam korrapärased, kuid dualide kaudu saab hästi mõista sümmeetriat ja nägude paiknemist. Praktikas kasutatakse Archimedean solids'i mudelina arhitektuuris, kristallograafias, põnevuse- ja hariduslike geomeetriamudelite kujundamisel ning ka teoreetilistes uurimustes sümmeetriast ja gruppide teatest tulenevate omaduste demonstreerimiseks.

Arhimedese hulktahuka konstrueerimiseks piisab tihti vähemalt kahest erinevast korrapärasest hulknurgast, mis esinevad tahkidena — see ongi üks asjaolu, mis eristab neid Platoniliste tahukate lihtsamast struktuurist.

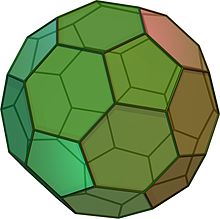
Lõigatud ikosaeeder näeb välja nagu jalgpall. See koosneb 12 võrdkülgsest viisnurksest ja 20 korrapärasest kuusnurksest. Sellel on 60 tippu ja 90 serva. See on arhimedese tahkis.

Omadused

Arhimedeuse ruumid koosnevad regulaarsetest hulknurkadest, seega on kõik servad ühesuguse pikkusega.
Kõik arhimedeuslike tahkete kehade kehad on võimalik toota platoonilistest tahkete kehadest, "lõigates servi" platoonilise tahke keha.
Nurgas ("tipus") kohtuvate hulknurkade tüüp iseloomustab nii arhimedese kui ka platoonilise tahke keha.

Seos platooniliste tahkete kehadega

Platoonilisi tahkeid kehasid saab muuta arhimedese tahkeks, järgides nende konstrueerimise reegleid.

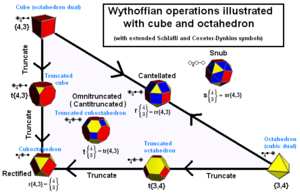
Archimedeans'i tahkiseid võib konstrueerida kaleidoskoobi generaatorite positsioonidena.

Arhimedeuse tahkete kehade loend

Järgnevalt on loetletud kõik arhimedeuslike tahkete kehade loetelud.

Pilt	Nimi	Faces	Tüüp	Servad	Vertikaalid
	Lõigatud tetraeeder	8	4 kolmnurka 4 kuusnurka	18	12
	Kuuboktaeder	14	8 kolmnurka 6 ruutu	24	12
	Katkendatud kuup	14	8 kolmnurka 6 kaheksanurkset	36	24
	Lõigatud oktaeder	14	6 ruutu 8 kuusnurka	36	24
	Rombikuboktaeder	26	8 kolmnurka 18 ruutu	48	24
	Katkendatud kuuboktaeder	26	12 ruutu 8 kuusnurka 6 kaheksanurkset	72	48
	Snub cube (2 peegelversiooni)	38	32 kolmnurka 6 ruutu	60	24
	Ikosidodekaeeder	32	20 kolmnurka 12 viisnurka	60	30
	Lõigatud dodekaeeder	32	20 kolmnurka 12 kümnendit	90	60
	Lõigatud ikosaeeder	32	12 viisnurka 20 kuusnurka	90	60
	Rombikosidodekaeedri	62	20 kolmnurka30 ruutu12 viisnurka	120	60
	Lõigatud ikosidodekaeeder	62	30 ruutu 20 kuusnurka 12 kümnendit	180	120
	Snub dodekaeeder (2 peegelversiooni)	92	80 kolmnurka 12 viisnurka	150	60

Küsimused ja vastused

K: Mis on arhimedese tahkis?

V: Archimedese tahkis on hulknurkadest koosnev kumer kuju, mille omadused on, et iga tahk on korrapärane hulknurk, kõik nurgad näevad välja ühesugused ja mis ei ole platooniline tahkis, prisma ega antiprisma.

Küsimus: Kui palju on arhimedeuslike tahkete kehade arvu?

V: Sõltuvalt sellest, kuidas neid loendatakse, on arhimedeuslike tahkete kehade arv kolmteist või viisteist.

K: Kes avastas arhimedeuse tahkised?

V: Arhimedeuse tahkised on saanud oma nime Vana-Kreeka matemaatiku Archimedese järgi, kes avastas need tõenäoliselt 3. sajandil eKr.

K: Mida tegi Pappus Aleksandriast Archimedese kirjutistega?

V: Pappus Aleksandriast võttis 4. sajandil kokku Archimedese kirjutised Archimedese tahkete kehade kohta.

K: Miks avastasid kunstnikud ja matemaatikud renessansiajal arhimedeuse tahkete kehade taas üles?

V: Renessansi ajal hindasid kunstnikud ja matemaatikud puhtaid vorme ning arhimedeuse tahkiseid peeti puhtaks vormiks.

K: Millal lõpetas Johannes Kepler kõigi arhimedeuslike tahkete kehade otsimise?

V: Johannes Kepler lõpetas tõenäoliselt kõigi arhimedeuslike tahkete kehade otsimise 1620. aasta paiku.

K: Mida on vaja arhimedeuse tahkise konstrueerimiseks?

V: Arhimedeuse ruumikuju konstrueerimiseks on vaja vähemalt kahte erinevat hulknurka.