Magnetiline moment (magnetdipoolmoment) – definitsioon, valem ja omadused

Magneti magnetmoment on vektoriaalne suurus, mis iseloomustab selle võimet mõjutada teisi magnetilisi objektideid ja elektrivoolu. See määrab ära jõu, mida magnet suudab avaldada voolule ning pöördemomendi, mida sellele avaldab magnetväli. Magnetiline moment esineb mitmel skaalal: elektrivoolusilmusel, vardamagnetil, elektronil, molekulil ja planeedil — kõikidel neil on omad magnetmomendi komponendid.

Nii magnetmomenti kui ka magnetvälja käsitletakse vektoriteks, millel on suurus ja suund. Magnetmomendi suund on väljapoole suunatud nii, et ühesuunalise dipooli puhul osutab vektori telg magneti „põhjapooli“ suunas (välisvaates lõunast põhja). Magneti tekitatud dipoolväli on proportsionaalne tema magnetmomendiga ja dipoolkomponent domineerib kaugel asuvates väliolukordades. Täpsemalt viitab mõiste magnetmoment tavaliselt süsteemi magnetilisele dipoolmomendile, mis on multipoolpaisutuse esimene (dominantne) term — selle väljapaisutus langeb kauguse kasvades vastavalt 1/r³.

Valemid ja tähtsaimad seosed

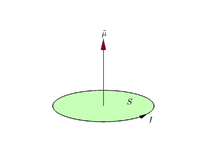
Praegusvoolu silmuse magnetdipoolmoment: μ = I·A. Siin I on vool tugevus ja A on suunatud pindala-vektor (A = S·n, kus S on pindala ja n normaalvektor). Magnetmoment on vektor, mille suund annab pindala normaali (õiguskäe reegel: kui sõrmed järgivad voolu suunda, osutab pöial magnetmomendi suunda).
Magnetiline pöördemoment väljas B: τ = μ × B. See väljendab vektoriaalset pöördemomenti, mis üritab joondada dipooli magnetvälja suunaga.
Potentsiaalne energia homogeenises väljas: U = −μ · B. Dipool on stabiilne, kui μ on risti vastava välja suunaga (sihitud samasuunaliselt annab madalama energia).
Magnetväli dipooli kaugusel r (valem SI ühikutes): B(r) = (μ0/4π) [ (3 r (μ · r) / r⁵) − μ / r³ ], kus μ0 on vaakumi permeabiilsus. See kirjeldus kehtib dipooli kaugelväljas (r palju suurem kui dipooli füüsiline mõõde).

Ühik ja skaalad

SI-ühik: A·m² (amper-ruutmeeter). Magnetmoment on ka mõõdetav energia per magnetväli ühikuna: J/T (džeul tesla kohta) — need kaks ühikut on võrdväärsed.
Elektroni magnetmoment ja Bohr-i magneton: kvantmehaaniliselt defineeritud ühe elektroni tüüpiline mõõt on Bohr-i magneton μB = eħ / (2 m_e) ≈ 9.274×10⁻²⁴ A·m². Elektroni spinniga seotud moment on sageli μ = −g (e/2m_e) S, kus g on g-faktor ja S on spinivektor; negatiivne märk tuleneb elektroni negatiivsest laengust.
Makroskoopilisel skaalal ulatuvad magnetmomendid tugevate püsimagentide, elektromagnetite ja planeetide puhul väga erinevatesse suurustesse — näiteks Maa magnetmoment tekib sügavatel elektrivooludel ja on palju suurem kui üksikmolekuli moment.

Omadused ja märkused

Dipoolkomponent domineerib kaugel väljadel; higher multipoolid (kvadrupool, okta pool jms) vähenavad kaugusel kiiremini.
Magnetiline moment jaotusena ruumalas: kogu magnetmoment M_tot = ∫ magnetisatsioon M(r) dV. Siin M(r) on magnetisatsioon (magnetmoment ruumalaühiku kohta).
Püsivad magnetid (ferromagnetilised esemendid) tekivad paljude mikro-dipoolide (elektronide orbital- ja spinnmomendi) kollektiivse joondumise tulemusena.
Elektroni ja aatomite magnetmomendid on kvantmehaanilised: need on kvantiseeritud ja sõltuvad orbitaal- ning spin-olekutest ning vastavatest g-faktoritest.
Suund ja märgis võivad eri juhtudel erineda: näiteks klassikalise noolekujulise dipooli puhul osutab vektor väljaspool magneti lõunast põhja, kuid elektroniga seotud μ on tihti vastassuunaline spinnile seotule tõttu laengu märgile.

Kasutusvaldkonnad ja tähtsus

Magnetmomendi mõistet kasutatakse laialdaselt füüsikas ja inseneriteaduses: magnetresonantsis (NMR, MRI), magnetomeetria mõõtmistes, materjaliteaduses (püsimagnetite ja ferromagnetiliste omaduste uurimine), astrofüüsikas (planeetide ja tähtede magnetväljade hindamine) ning kvanttehnoloogiates (spin-põhised kvabitid jt). Dipoolmoment annab lihtsa ja kasuliku lähendi süsteemi magnetvälja kaugvälja kirjeldamiseks.

Kaks hetke määratlust

Õpikutes kasutatakse magnetmomendi määratlemiseks kahte teineteist täiendavat lähenemist. Enne 1930. aastaid koostatud õpikutes määratleti neid magnetiliste pooluste abil. Enamik uuemaid õpikuid määratlevad neid ampeeriumi voolude abil.

Magnetpooluse määratlus

Füüsikud kujutavad materjalide magnetmomendi allikaid poolustena. Põhja- ja lõunapoolused on analoogia positiivse ja negatiivse laengu jaoks elektrostaatikas. Mõelgem baarimagnetile, millel on võrdse suurusega, kuid vastupidise polaarsusega magnetpoolused. Kumbki poolus on magnetilise jõu allikas, mis nõrgeneb kauguse kasvades. Kuna magnetpoolused on alati paarikaupa, siis nende jõud osaliselt tühistavad teineteist, sest kui üks poolus tõmbab, siis teine tõukab. See tühistamine on suurim, kui poolused on üksteisele lähedal, st kui vardamagnet on lühike. Seega sõltub magnetjõud, mida vardamagnet tekitab teatavas ruumipunktis, kahest tegurist: nii pooluste tugevusest p {\displaystyle p} $p$ kui ka vektorist l {\displaystyle \mathbf}. }, mis neid lahutab $\mathbf {l}$ . Moment on defineeritud järgmiselt

m = p l . {\displaystyle \mathbf {m} =p\mathbf {l} . } $\mathbf {m} =p\mathbf {l} .$

See näitab lõunapooluse suunas põhja pooluse suunas. Analoogiat elektrilise dipooliga ei tohiks liiga kaugele minna, sest magnetilised dipoolid on seotud nurkkiirusega (vt Magnetiline moment ja nurkkiirus). Sellegipoolest on magnetpoolused väga kasulikud magnetostaatilistes arvutustes, eriti ferromagnetite rakendustes. Praktikud, kes kasutavad magnetpooluste meetodit, kujutavad magnetvälja tavaliselt irrotatsioonivälja H {\displaystyle \mathbf {H} abil. } $\mathbf {H}$ analoogselt elektriväljaga E {\displaystyle \mathbf {E} } $\mathbf {E}$ .

Praeguse tsükli määratlus

Oletame, et tasapinnaline suletud silmus kannab elektrivoolu I {\displaystyle I} ja sellel on vektori pindala S {\displaystyle \mathbf {S} } $\mathbf {S}$ ( x {\displaystyle x} , y {\displaystyle y} , ja z {\displaystyle z} $z$ selle vektori koordinaadid on silmuse projektsioonide pindalad y z {\displaystyle yz} peale. $yz$ , z x {\displaystyle zx} $zx$ ja x y {\displaystyle xy} $xy$ tasandid). Selle magnetiline moment m {\displaystyle \mathbf {m} } $\mathbf {m}$ , vektor, on defineeritud järgmiselt:

m = I S . {\displaystyle \mathbf {m} =I\mathbf {S} . } $\mathbf {m} =I\mathbf {S} .$

Konventsiooni kohaselt on vektorala suund antud parema käe haaramisreegliga (parema käe sõrmede kõverdamine voolu suunas ümber silmuse, kui peopesa "puudutab" silmuse välisserva, ja sirge pöial näitab vektorala ja seega magnetmomendi suunda).

Kui silmus ei ole tasapinnaline, siis on moment antud kui

m = I ∫2 r × d r . {\displaystyle \mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \times {\rm {d}}\mathbf {r} . } $\mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \times {\rm {d}}\mathbf {r} .$

Kõige üldisemal juhul, kui tegemist on suvalise voolujaotusega ruumis, saab sellise jaotuse magnetmomendi leida järgmise võrrandi abil:

m = ∫12 r × J d V , {\displaystyle \mathbf {m} ={\frac {1}{2}}\int \mathbf {r} \times \mathbf {J} \,\rm {d}}V,} $\mathbf {m} ={\frac {1}{2}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}V,$

kus r {\displaystyle \mathbf {r} } $\mathbf {r}$ on asukohavektor, mis näitab alguspunktist ruumala elemendi asukoha suunas, ja J {\displaystyle \mathbf {J} } $\mathbf {J}$ on voolutiheduse vektor selles asukohas.

Ülaltoodud võrrandit saab kasutada mis tahes liikuvate laengute kogumiku, näiteks pöörleva laetud tahke keha magnetmomendi arvutamiseks, asendades selle järgmiselt

J = ρ v , {\displaystyle \mathbf {J} =\rho \mathbf {v} ,} $\mathbf {J} =\rho \mathbf {v} ,$

kus ρ {\displaystyle \rho } $\rho$ on elektrilaengu tihedus antud punktis ja v {\displaystyle \mathbf {v} } $\mathbf {v}$ on selle punkti hetkeline lineaarne kiirus.

Näiteks ringikujulisel teel liikuva elektrilaengu tekitatud magnetiline moment on

m = q12 r × v {\displaystyle \mathbf {m} ={\frac {1}{2}}\,q\,\mathbf {r} \times \mathbf {v} } $\mathbf {m} ={\frac {1}{2}}\,q\,\mathbf {r} \times \mathbf {v}$ ,

kus r {\displaystyle \mathbf {r} } $\mathbf {r}$ on laengu q {\displaystyle q} asukoht ringi keskpunkti suhtes ja v {\displaystyle \mathbf {v} } $\mathbf {v}$ on laengu hetkeline kiirus.

Praktikud, kes kasutavad voolusilmuse mudelit, esitavad magnetvälja tavaliselt solenoidvälja B {\displaystyle \mathbf {B} abil. } $\mathbf {B}$ analoogselt elektrostaatilise väljaga D {\displaystyle \mathbf {D} } $\mathbf {D}$ .

Solenoidi magnetiline moment

Eespool kirjeldatud vooluahela üldistus on mitme pöörde mähis ehk solenoid. Selle moment on üksikute keerdude momentide vektorsumma. Kui solenoidil on N $N$ identset keerdu (üheahelaline mähis),

m = N I S . {\displaystyle \mathbf {m} =NI\mathbf {S} . } $\mathbf {m} =NI\mathbf {S} .$

3-D kujutis solenoidist.

Moment m {\displaystyle \mathbf {m} } $\mathbf {m}$ tasapinnalise vooluahela pindalaga S {\displaystyle S} $S$ ja vooluga I {\displaystyle I} .

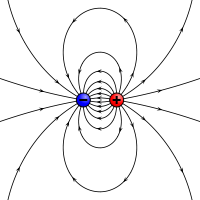
Magnetmomendi elektrostaatiline analoog: kaks vastandlikku laengut, mida lahutab piiratud vahemaa.

Units

Magnetmomendi ühik ei ole rahvusvahelise mõõtühikute süsteemi (SI) põhiühik ja seda saab esitada rohkem kui ühel viisil. Näiteks vooluahela määratluses mõõdetakse pindala ruutmeetrites ja I {\displaystyle I} amprites, seega mõõdetakse magnetmomenti amper-ruutmeetrites ( A m {\displaystyle2 {\text{A m}^{2}} ${\text{A m}}^{2}$ ). Momendi pöördemomendi võrrandis mõõdetakse pöördemomenti njuutonmeetrites ja magnetvälja teslates, seega mõõdetakse momenti N.m tesla kohta ( N.m T - 1{\displaystyle {\text{N.m T}}^{-1}} ${\text{N.m T}}^{-1}$ ). Need kaks esitusviisi on samaväärsed:

A m =2 N.m T -1 . {\displaystyle \,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}. } $\,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}.$

CGS-süsteemis on mitu erinevat elektromagnetismiüksuste komplekti, millest peamised on ESU, Gaussi ja EMU. Nende hulgas on CGSis kaks alternatiivset (mitte-ekvivalentset) magnetilise dipoolmomendi ühikut:

(ESU CGS) 1 statA-cm² = 3,33564095×10^-14 (m-A² või N.m/T)

ja (sagedamini kasutatav)

(EMU CGS ja Gaussi-CGS) 1 erg/G = 1 abA-cm² = 10^-3 (m-A² või N.m/T).

Nende kahe mitte-ekvivalentse CGS-ühiku (EMU/ESU) suhe on täpselt võrdne valguse kiirusega vabas ruumis, väljendatuna cm/s.

Kõik käesolevas artiklis esitatud valemid on korrektsed SI-ühikutes, kuid teistes ühikusüsteemides võib olla vaja valemeid muuta. Näiteks SI-ühikutes on voolusilmusel, mille voolutugevus on I ja pindala A, magnetmoment I×A (vt allpool), kuid Gaussi ühikutes on magnetmoment I×A/c.

Mõnede elementaarosakeste olemuslikud magnetmomendid ja spinnid
Osakeste	Magnetiline dipoolmoment SI-ühikutes (10 ⁻²⁷J/T)	Spinni kvantarv (dimensioonita)
elektron	-9284.764	1/2
prooton	14.106067	1/2
neutron	-9.66236	1/2
muon	-44.904478	1/2
deuteroon	4.3307346	1
triton	15.046094	1/2

Magnetmomendi ja magnetiseerimise mõistete vahelise seose kohta vt magnetiseerimine.

Küsimused ja vastused

K: Mis on magneti magnetiline moment?

V: Magneti magnetmoment on suurus, mis määrab ära jõu, mida magnet suudab avaldada elektrivoolule, ja pöördemomendi, mida magnetväli sellele avaldab.

K: Millistel objektidel on magnetiline moment?

V: Elektrivoolusilmus, staabimagnet, elektron, molekul ja planeet on kõik magnetmomendid.

K: Kuidas saab käsitleda nii magnetmomenti kui ka magnetvälja?

V: Nii magnetmomenti kui ka magnetvälja võib käsitleda vektoritena, millel on suurus ja suund.

K: Millises suunas näitab magnetmoment magnetis?

V: Magnetmomendi suund näitab magneti lõunapoolusest põhjapoolusele.

K: Milline on magnetmomendi ja magnetvälja vaheline seos?

V: Magneti tekitatud magnetväli on proportsionaalne tema magnetilise momendiga.

K: Mida tähistab tavaliselt mõiste magnetmoment?

V: Täpsemalt öeldes viitab mõiste magnetmoment tavaliselt süsteemi magnetilisele dipoolmomendile, mis tekitab esimese termini üldise magnetvälja multipoolpaisutuses.

K: Kuidas käitub objekti magnetvälja dipoolkomponent, kui kaugus objektist suureneb?

V: Objekti magnetvälja dipoolkomponent on sümmeetriline tema magnetilise dipoolmomendi suuna suhtes ja väheneb objektist kauguse pöördkuubiku võrra.