AlegsaOnline.com

Gravitatsioonikiirendus (g) — määratlus, väärtus ja mõju (9,80665 m/s²)

Gravitatsioonikiirendus (g), 9,80665 m/s²: selgitus, mõju vabale langemisele, Maa pinnaväärtuste erinevused ja praktilised näited — kiire ja arusaadav ülevaade.

Autor: Leandro Alegsa

30-08-2025

Kiirendust, mille objekt saab gravitatsioonijõu tõttu, nimetatakse gravitatsioonikiirenduseks. Selle SI-ühik on m/s². Gravitatsioonikiirendus on vektor, mis tähendab, et sellel on nii suurus kui ka suund — suunatud üldjuhul massikeskme poole. Maa pinnal tähistatakse seda tähega g. Selle standardväärtus on 9,80665 m/s² (32,1740 ft/s²), kuid vabalt langeva keha tegelik kiirendus sõltub asukohast ja tingimustest.

Standardväärtus ja valem

Standardne (normaalne) gravitatsioon, mida sageli tähistatakse g₀, on määratletud kui 9,80665 m/s² ja kasutatakse kalibreerimisel ning tehnilistes tabelites. Gravitatsioonikiirenduse teoreetiline väärtus punktis kaugusel r massist M arvutatakse Newtoni seaduse abil:

g = G·M / r²,

kus G on universaalne gravitatsioonikonstant. Maa pinnal määrab g nii Maa mass kui ka kaugus Maa keskpunktist.

Kuidas g varieerub

Kõrgus (h): g väheneb kõrguse kasvades ligikaudu vastavalt seadusele g(h) ≈ g0·(1 − 2h/R) väikeste h puhul (R on Maa raadius). Praktiliselt tähendab see umbes −0,00309 m/s² muutust iga tõusu kohta 1 km võrra (ligikaudu −3,09·10⁻³ m/s²/km).
Laiuskraad: Maa pöörlemine ja ekvaatori paisutatus tekitavad erinevusi — g on suurem polaarpiirkondades ja väiksem ekvaatoril. Tüüpiline erinevus neemete vahel on ~0,052 m/s² (polaaril ~9,832 m/s², ekvaatoril ~9,780 m/s²).
Lokaalne geoloogia: Maa kooriku tiheduse erinevused (mäestikud, maaväätmed, varud jm) võivad kohalikult muuta g väärtust väikestes piirides.
Tsentrifugaalne efekt: Maa pöörlemisest tulenev tsentrifugaaljõud vähendab näivat gravitatsioonikiirendust eriti ekvaatoril.

Mõõtmine

Gravitatsioonikiirendust mõõdetakse gravimeetritega ja täppismõõtmised võimaldavad tuvastada väga väikseid muutusi (10⁻⁸…10⁻⁶ m/s²). Universaalse gravitatsioonikonstandi G täpne määramine tuli ajaloo jooksul läbi eksperimendi (Cavendish), mille abil saab seejärel hinnata g väärtust antud massi ja kauguse korral.

Mõju igapäevaelule ja tehnilistes arvutustes

Kaal: Kehale mõjuv kaaljõud on F = m·g — ehk suurem g annab suurema kaalu samal massil.
Püstitööde ja inseneriõpingud: hooned, sillad ja masinad projekteeritakse arvestusega kohaliku g väärtuse ning võimalike muutuste suhtes.
Ballistika ja lennundus: lennuteekonnad, laskemoona trajektoorid ja satelliitide stardikalkulatsioonid sõltuvad gravitatsioonist ning selle täpsest arvestusest.
Vabalt langevad keha ja õhutakistus: õhus langeval objektil on algne kiirendus ligikaudu g, kuid õhutakistus viib lõpuks lõppkiiruseni (terminal velocity), kus takistusjõud võrdub raskusjõuga.

Võrdlused teiste taevakehadega

Maa g on 9,80665 m/s². Näited: Kuu pinnal on g ≈ 1,622 m/s² (≈0,165·Maa g), Marsil ≈ 3,72076 m/s². Kuigi teistel planeetidel on suurem mass, mõjutab ka nende raadius tulemuseks tekkiv g.

Kokkuvõte

Gravitatsioonikiirendus on fundamentaalne füüsikaline suurus, mis määrab, kuidas massid üksteist tõmbavad ja kuidas langevad keha Maa lähedal. Kuigi standardväärtus 9,80665 m/s² on laialt kasutusel, võib tegelik g kohati erineda kõrguse, laiuskraadi, Maa pöörlemise ja kohaliku geoloogia tõttu. Täpsed mõõtmised ja arvestused on olulised nii teaduses kui ka igapäevastes tehnilistes rakendustes.

Miks raskemad objektid ei lange kiiremini kui kergemad objektid

Isaac Newton arvutas välja, et resultantjõud on võrdne massi ja kiirenduse korrutisega ehk sümbolitega F = m a {\displaystyle F=ma} $F=ma$ . Seda saab ümber korraldada, et saada a = F m {\displaystyle a={\frac {F}{m}}\ }\ } $a={\frac {F}{m}}\$ . Mida suurem on langeva objekti mass, seda suurem on gravitatsiooniline tõmbejõud, mis tõmbab seda Maa poole. Ülaltoodud võrrandis on see F {\displaystyle F} . Kuid see, mitu korda muutub jõud suuremaks või väiksemaks, on võrdne sellega, mitu korda muutub mass suuremaks või väiksemaks, kusjuures suhe jääb konstantseks. Igas olukorras tühistub F m {\displaystyle {\frac {F}{m}}} ${\frac {F}{m}}\$ ühtlase kiirenduseni, mis on umbes 9,8 m/s² . See tähendab, et kõik vabalt langevad objektid kiirenevad sõltumata nende massist ühtlaselt.

Vaadake järgmisi näiteid:

a = 49 N 5 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} } $a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}}$

a = 147 N 15 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} } $a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}}$

Pinnakiirendus

Sõltuvalt asukohast langeb objekt Maa pinnal kiirendusega 9,76-9,83 m/s² (32,0-32,3 ft/s² ).

Maa ei ole täpselt kerakujuline. See sarnaneb "kokkusurutud" kerale, mille raadius ekvaatoril on veidi suurem kui raadius poolustel. Selle tagajärjel suureneb gravitatsioonikiirendus poolustel veidi (kuna me oleme Maa keskmele lähedal ja gravitatsioonijõud sõltub kaugusest) ja väheneb ekvaatoril veidi (kuna me oleme Maa keskmele lähedal ja gravitatsioonijõud sõltub kaugusest). Samuti on tsentripetaalkiirenduse tõttu gravitatsioonikiirendus ekvaatoril veidi väiksem kui poolustel. Maapinna all oleva kivimi tiheduse muutused või läheduses asuvate mägede olemasolu võivad gravitatsioonikiirendust veidi mõjutada.

Kõrgus

Objekti kiirendus muutub koos kõrgusega. Gravitatsioonikiirenduse muutumine Maa keskpunktist kaugenedes järgib pöördruutu seadust. See tähendab, et gravitatsioonikiirendus on pöördvõrdeline Maa keskpunktist kauguse ruuduga. Kui kaugus kahekordistub, väheneb gravitatsioonikiirendus 4 korda, kui kaugus kolmekordistub, väheneb gravitatsioonikiirendus 9 korda jne.

gravitatsioonikiirendus ∝ 1 kaugus 2 {\displaystyle {\mbox{gravitatsioonikiirendus}\ \propto \ {\frac {1}{{{\mbox{kaugus}}^{2}}}}\ }\ ${\mbox{gravitational acceleration}}\ \propto \ {\frac {1}{{\mbox{distance}}^{2}}}\$

gravitatsioonikiirendus × kaugus 2 = k {\displaystyle {\mbox{gravitatsioonikiirendus}}\ \times {{\mbox{kaugus}}^{2}}\ ={k}} ${\mbox{gravitational acceleration}}\ \times {{\mbox{distance}}^{2}}\ ={k}$

Maa pinnal on raskuskiirendus ligikaudu 9,8 m/s² (32 ft/s² ). Keskmine kaugus Maa keskpunktist on 6 371 km (3 959 mi).

k = 9.8 × 6371 2 {\displaystyle {k}={\mbox{9.8}}\ \times {{\mbox{6371}}}^{2}}} ${k}={\mbox{9.8}}\ \times {{\mbox{6371}}^{2}}$

Kasutades konstanti k {\displaystyle k} saame välja arvutada gravitatsioonikiirenduse teatud kõrgusel.

gravitatsioonikiirendus = k kaugus 2 {\displaystyle {\mbox{gravitatsioonikiirendus}}\ ={\frac {k}{{\mbox{kaugus}}^{2}}}\ }\ } ${\mbox{gravitational acceleration}}\ ={\frac {k}{{\mbox{distance}}^{2}}}\$

Näide: Leia raskuskiirendus 1000 km (620 mi) kõrgusel Maa pinnast.

6371 + 1000 = 7371 {\displaystyle 6371+1000=7371} $6371+1000=7371$

∴ Kaugus Maa keskpunktist on 7371 km.

gravitatsioonikiirendus = 9.8 × 6371 2 7371 2 ≈ 7.3 {\displaystyle {\mbox{gravitatsioonikiirendus}\ =\frac {\mbox{9.8}\ \times {\mbox{6371}}^{2}}}{{\mbox{7371}}^{2}}}}\ \approx 7.3}} ${\mbox{gravitational acceleration}}\ ={\frac {{\mbox{9.8}}\ \times {{\mbox{6371}}^{2}}}{{\mbox{7371}}^{2}}}\ \approx 7.3$

∴ Gravitatsioonist tingitud kiirendus 1000 km (620 mi) kõrgusel Maa pinnast on 7,3 m/s² (24 ft/s² ).

Gravitatsioonikiirendus Kármáni joonel, Maa atmosfääri ja kosmose vahelisel piiril, mis asub 100 km kõrgusel, on ainult umbes 3% madalam kui merepinnal.

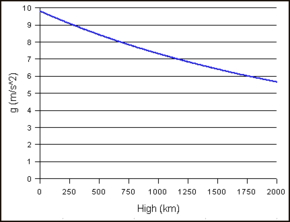
Gravitatsioonikiirenduse muutus koos objekti kõrgusega

Küsimused ja vastused

K: Mis on raskuskiirendus?

V: Gravitatsioonist tingitud kiirendus on kiirendus, mille objekt saab gravitatsioonijõu tõttu.

K: Mis on raskuskiirenduse SI-ühik?

V: Gravitatsioonikiirenduse SI-ühik on m/s2.

K: Kas raskuskiirendus on skalaar või vektor?

V: Gravitatsioonikiirendus on vektor, sest sellel on nii suurus kui ka suund.

K: Millise sümboliga tähistatakse raskuskiirust Maa pinnal?

V: Maa pinnal esineva raskuskiirenduse tähistamiseks kasutatav sümbol on g.

K: Milline on raskuskiirenduse standardväärtus Maa pinnal?

V: Maa pinnal on raskuskiirenduse standardväärtus 9,80665 m/s2 (32,1740 ft/s2).

K: Kas vabalt langeva keha tegelik kiirendus muutub sõltuvalt asukohast?

V: Jah, keha tegelik kiirendus vabalangemisel muutub sõltuvalt asukohast.

K: Mis on raskuskiirenduse definitsioon?

V: Gravitatsioonikiirendus on kiirendus, mille objekt saab gravitatsioonijõu mõjul ja mida kujutatakse tähega g, mille standardväärtus on 9,80665 m/s2 Maa pinnal, samas kui tegelik kiirendus võib sõltuvalt asukohast erineda.