AlegsaOnline.com

Mis on standardhälve? Lihtne definitsioon, valem ja näited

Mõista standardhälvet kiiresti: lihtne definitsioon, valem ja selged näited õpilastele, teadlastele ja finantsotsustajatele.

Autor: Leandro Alegsa

14-10-2025

Standardhälve näitab, kui palju andmepunktid või mõõtmised erinevad rühma keskväärtusest (keskmisest) või oodatavast väärtusest. Madal standardhälve tähendab, et enamik väärtusi on keskmisele lähedal; suur standardhälve tähendab, et väärtused on tugevamalt hajutatud ehk üksteisest ja keskmisest kaugel.

On oluline eristada standardhälvet ja standardviga. Standardhälve mõõdab andmete hajuvust individuaalses andmekogus, standardviga (standard error, SE) mõõdab keskmise hinnanguvõrra usaldusväärsust: SE = s / sqrt(n), kus s on valimi standardhälve ja n on vaadeldud andmepunktide arv. Teadlased kasutavad katsetes sageli valimi standardhälvet, et kirjeldada, kui palju üksikud tulemused erinevad keskmisest; seejärel hinnatakse standardvea abil, kui täpne on see keskmise hinnang. Sageli peetakse ainult neid erinevusi statistiliselt olulisteks, mis on mitu korda suuremad kui standardviga — näiteks umbes kaks korda suurem standardviga annaks ligikaudse 95% usaldusintervalli. . Standardhälvet kasutatakse ka raha ja finantsnäitajate puhul: intressi või tootluse standardhälve näitab, kui palju ühe isiku teenitud intress või tootlus võib erineda keskmisest.

Sageli on võimalik mõõta ainult osa kogu grupist ehk valimit. Sellisel juhul kasutatakse valimi standardhälbe valemit (milles jagamisel kasutatakse n−1), et saada eelarve, mis annab parema hinnangu kogu populatsiooni standardhälbele — seda nimetatakse Besseli korrigeerimiseks (degrees of freedom ehk vabadusastmete arvestus). Allpool selgitan valemeid ja toon lihtsad näited.

Valemid

Populatsiooni standardhälve (kui teil on kõik populatsiooni andmed): σ = sqrt( (1/N) * Σ(xi − μ)² ), kus N on kogu populatsiooni suurus, μ on populatsiooni keskmine ja xi on iga andmepunkt.
Valimi standardhälve (kui teil on ainult valim): s = sqrt( (1/(n−1)) * Σ(xi − x̄)² ), kus n on valimi suurus ja x̄ on valimi keskmine. Jagamine n−1-ga (Besseli korrigeer) annab vääritumatta paremaks hinnanguks populatsiooni variatsioonile.

Lihtne näide — samm-sammult

Oletame, et meil on andmed: 4, 7, 13, 16. Arvutame valimi standardhälbe (käsitleme neid kui valimit):

Leia keskmine: x̄ = (4 + 7 + 13 + 16) / 4 = 40 / 4 = 10.
Leia iga väärtuse erinevus keskmisest ja ruut: (4−10)² = 36; (7−10)² = 9; (13−10)² = 9; (16−10)² = 36.
Summa: 36 + 9 + 9 + 36 = 90.
Jagame n−1 = 4−1 = 3: 90 / 3 = 30.
Standardhälve s = sqrt(30) ≈ 5.477.

Kui need sama andmed moodustaksid kogu populatsiooni (N = 4), oleks populatsiooni standardhälve σ = sqrt(90 / 4) = sqrt(22.5) ≈ 4.743.

Tõlgendamine ja omadused

Standardhälve on väljendatud samades ühikutes kui algandmed (näiteks eurot, kilogrammi või punkte), mistõttu on seda lihtne tõlgendada.
Variance (variatsioon) on standardhälbe ruut: varians = σ² (populatsioon) või s² (valim). Variants on matemaatiliselt mugavam, aga üksustelt erinev (ruutühikud).
Kui andmed on normaalselt jaotunud, annab standardhälve reegli 68–95–99.7: umbes 68% väärtustest jääb ±1σ piiresse, 95% ±2σ ja 99.7% ±3σ piiresse.
Väärtuste erinevus olulisuse hindamiseks kasutatakse sageli standardviga ja usaldusvahemikke: standardviga on standardhälve jagatud ruutjuurega n-st (SE = s/√n) ning 95% usaldusvahemiku ligikaudne marginaal on ≈ 1.96·SE.

Praktilised näpunäited ja levinud vigad

Ära segi aja standardhälvet ja standardviga — esimene mõõdab hajuvust andmestikus, teine mõõdab keskmise täpsust.
Kui kasutad valimi andmeid, kasuta valimi standardhälbe valemit (n−1), eriti kui eesmärk on hinnata populatsiooni variatsiooni.
Standardhälve on tundlik äärmuslike väärtuste (outlierite) suhtes — üks väga suur või väga väike väärtus võib standardhälvet märgatavalt suurendada.

Kui soovid, saan arvutada standardhälbe sinu antud andmekogule sammuhaaval või selgitada, kuidas seda teha Excelis, R-is või kalkulaatoriga.

Normaaljaotuse graafik (või kellukõver). Iga värviline riba on ühe standardhälbe laiune.

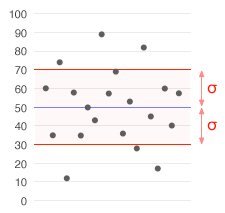
Andmekogum, mille keskmine on 50 (näidatud sinisega) ja standardhälve (σ) on 20.

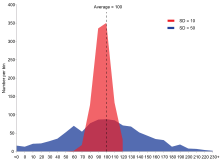
Näide kahe sama keskmise ja erineva standardhälbega valimipopulatsiooni kohta. Punase populatsiooni keskmine on 100 ja SD 10; sinise populatsiooni keskmine on 100 ja SD 50.

Põhinäide

Vaadelda rühma, millel on järgmised kaheksa numbrit:

2 , ,4 , ,4 , ,4 , 5, 5, 7{\displaystyle9 2,\ 4,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9} $2,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9$

Nende kaheksa numbri keskmine (keskmine) on 5:

2 + +4 + +4 + +4 +5 + + 5+ 7= 98{\displaystyle5 {\frac {2+4+4+4+4+5+5+7+9}{8}}=5} ${\frac {2+4+4+4+5+5+7+9}{8}}=5$

Populatsiooni standardhälbe arvutamiseks leiate kõigepealt iga numbri erinevuse keskmisest. Seejärel ruudutatakse iga erinevuse tulemus:

( 2- 5) =2 ( - 3) = 2(95 - 5) = 2= 02(04 - 5) =2 ( - 1) = 2(15 - 5) = 2= 02( 04-5 ) =2 ( - ) = ( - 1) = 2(17 - 5) = 2= 22( 44- 5) =2 ( - ) = ( - 1) = 2(19 - 5) = = 242{\displaystyle16 {\begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}} ${\begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}$

Seejärel leiate nende väärtuste keskmise (summa jagatud numbrite arvuga). Viimasena võtke ruutjuur:

( +9 + +1 + +1 +1 + + 0+ + 0+ 4)16 = 8{\displaystyle2 {\sqrt {\frac {(9+1+1+1+1+0+0+4+16)}{8}}}=2} ${\sqrt {\frac {(9+1+1+1+0+0+4+16)}{8}}}=2$

Vastus on populatsiooni standardhälve. Valem on tõene ainult siis, kui kaheksa numbrit, millest alustasime, moodustavad kogu rühma. Kui need on vaid osa juhuslikult valitud grupist, siis peaksime eelviimase sammu alumisel (nimetajas) kasutama 7 (mis on n - 1), mitte 8 (mis on n). Siis on vastus valimi standardhälve. Seda nimetatakse Besseli korrektsiooniks.

Rohkem näiteid

Veidi raskem, reaalse elu näide: Ameerika Ühendriikide täiskasvanud meeste keskmine pikkus on 70", standardhälbega 3". Standardhälve 3" tähendab, et enamiku meeste (umbes 68%, eeldades normaaljaotust) pikkus on keskmisest (67"-73") 3" pikem kuni 3" lühem - üks standardhälve. Peaaegu kõik mehed (umbes 95%) on keskmisest (64"-76") 6" pikemad kuni 6" lühemad - kaks standardhälvet. Kolm standardhälvet hõlmavad kõiki numbreid 99,7% uuritava valimi populatsioonist. See kehtib juhul, kui jaotus on normaalne (kellukujuline).

Kui standardhälve oleks null, siis oleksid kõik mehed täpselt 70" pikad. Kui standardhälve oleks 20", siis oleksid mõned mehed keskmisest palju pikemad või palju lühemad, tüüpiline vahemik oleks umbes 50"-90".

Teise näite puhul on kolme rühma {0, 0, 14, 14}, {0, 6, 8, 14} ja {6, 6, 8, 8, 8} keskmine (keskmine) 7. Kuid nende standardhälbed on 7, 5 ja 1. Kolmanda rühma standardhälve on palju väiksem kui kahe teise rühma oma, sest nende arvud on kõik 7 lähedased. Põhiidee on, et standardhälve näitab, kui kaugel keskmisest kalduvad ülejäänud arvud olema. Sellel on samad ühikud kui numbritel endil. Kui näiteks rühm {0, 6, 8, 14} on nelja venna rühma vanused aastates, siis on keskmine 7 aastat ja standardhälve 5 aastat.

Standardhälve võib olla mõõtemääramatuse mõõdupuuks. Teaduses aitab näiteks korduvate mõõtmiste rühma standardhälve teadlastel teada, kui kindlad nad on keskmises arvus. Kui otsustatakse, kas eksperimendi mõõtmised vastavad prognoosile, on nende mõõtmiste standardhälve väga oluline. Kui katsete keskmine arv on liiga kaugel ennustatud arvust (kusjuures kaugust mõõdetakse standardhälvetes), siis ei pruugi testitav teooria olla õige. Vt ennustusintervall.

Näited rakenduste kohta

Väärtuste kogumi standardhälbe mõistmine aitab teada, kui suur on eeldatav erinevus "keskmisest" (keskmisest).

Ilm

Lihtsa näitena võib tuua kahe linna, ühe sisemaa ja teise ookeaniäärse linna keskmised päevased kõrged temperatuurid. On kasulik mõista, et ookeani lähedal asuvate linnade päevaste kõrgete temperatuuride vahemik on väiksem kui sisemaal asuvate linnade puhul. Nende kahe linna keskmine päevane kõrge temperatuur võib olla sama. Rannikulähedase linna päevase kõrge temperatuuri standardhälve on siiski väiksem kui sisemaal asuva linna oma.

Sport

Teine võimalus seda näha on vaadata spordimeeskondi. Igal spordialal on meeskondi, kes on mõnes asjas head ja mõnes mitte. Meeskonnad, mis on kõige kõrgemal kohal, ei näita suuri erinevusi võimetes. Nad teevad enamikus kategooriates hästi. Mida väiksem on nende võimekuse standardhälve igas kategoorias, seda tasakaalustatumad ja ühtlasemad nad on. Suurema standardhälbega meeskonnad on aga vähem ettearvatavad. Meeskonnal, kes on enamikus kategooriates tavaliselt kehv, on madal standardhälve. Meeskonnal, kes on enamikus kategooriates tavaliselt hea, on samuti madal standardhälve. Kõrge standardhälbega meeskond võib aga olla selline meeskond, mis teeb palju punkte (tugev rünnak), kuid laseb ka teisel meeskonnal palju punkte teha (nõrk kaitse).

Püüdes ette teada, millised meeskonnad võidavad, võib vaadata erinevate meeskondade "statistika" standardhälbeid. Arvud, mis erinevad oodatust, võivad sobitada tugevusi ja nõrkusi, et näidata, millised põhjused võivad olla kõige olulisemad, et teada saada, milline meeskond võidab.

Võidusõidus mõõdetakse aega, mis sõitjal kulub iga ringi läbimiseks. Sõitja, kelle ringiaegade standardhälve on väike, on järjepidevam kui sõitja, kelle standardhälve on suurem. Seda teavet saab kasutada selleks, et mõista, kuidas sõitja saab ringide läbimise aega vähendada.

Raha

Rahas võib standardhälve tähendada riski, et hind tõuseb või langeb (aktsiad, võlakirjad, kinnisvara jne). Samuti võib see tähendada riski, et hindade rühm tõuseb või langeb (aktiivselt juhitud investeerimisfondid, indeksfondid või ETFid). Risk on üks põhjus, miks teha otsuseid selle kohta, mida osta. Risk on number, mille abil inimesed saavad teada, kui palju raha nad võivad teenida või kaotada. Mida suuremaks muutub risk, seda suurem võib investeeringu tootlus olla oodatust suurem (standardhälve "pluss"). Samas võib investeeringu puhul ka raha kaotada oodatust rohkem (standardhälve "miinus").

Näiteks pidi inimene valima kahe aktsia vahel. Aktsia A oli viimase 20 aasta jooksul keskmiselt 10 protsendi tootlusega, mille standardhälve oli 20 protsendipunkti (pp). Aktsia B viimase 20 aasta keskmine tootlus oli 12 protsenti, kuid standardhälve oli suurem (30 protsendipunkti). Riskile mõeldes võib inimene otsustada, et aktsia A on turvalisem valik. Kuigi ta ei pruugi teenida nii palju raha, ei kaota ta tõenäoliselt ka palju raha. Isik võib arvata, et aktsia B 2 protsendipunkti võrra kõrgem keskmine ei ole väärt täiendavat 10 protsendipunkti standardhälvet (suurem risk või ebakindlus oodatava tootluse osas).

Normaalselt jaotunud arvude reeglid

Enamik standardhälbe matemaatilisi võrrandeid eeldab, et arvud on normaalselt jaotunud. See tähendab, et arvud on jaotunud teatud viisil mõlemal pool keskmist väärtust. Normaaljaotust nimetatakse ka Gaussi jaotuseks, sest selle avastas Carl Friedrich Gauss. Seda nimetatakse sageli kellakõveraks, sest arvud jaotuvad nii, et need moodustavad graafikul kellakujulise kuju.

Arvud ei ole normaaljaotusega, kui nad on rühmitatud keskväärtuse ühele või teisele poole. Arvud võivad olla hajutatud ja olla ikkagi normaalselt jaotunud. Standardhälve näitab, kui laialt on arvud hajutatud.

Tumesinine on vähem kui üks standardhälve keskmisest. Normaaljaotuse puhul hõlmab see 68,27 protsenti arvudest; samas kui kaks standardhälvet keskmisest (keskmine ja tumesinine) hõlmavad 95,45 protsenti; kolm standardhälvet (helesinine, keskmine ja tumesinine) hõlmavad 99,73 protsenti ja neli standardhälvet moodustavad 99,994 protsenti.

Keskmise (keskmine) ja standardhälbe vaheline seos

Andmekogumi keskmine (keskmine) ja standardhälve kirjutatakse tavaliselt koos. Siis saab inimene aru, milline on keskmine arv ja kui laialt on teised arvud rühmas hajutatud.

Seda, kuidas arvude rühm on jaotunud, võib anda ka variatsioonikordaja, mis on standardhälve jagatud keskmisega. See on mõõtmeta arv. Variatsioonikordaja korrutatakse sageli 100%-ga ja kirjutatakse protsendina.

Ajalugu

Terminit standardhälve kasutas kirjalikult esmakordselt Karl Pearson 1894. aastal pärast seda, kui ta seda loengutes kasutas. See oli sama idee varasemate nimetuste asenduseks: näiteks Gauss kasutas keskmist viga.

Seotud leheküljed

Täpsus ja täpsus
Valimi suurus

Küsimused ja vastused

K: Mis on standardhälve?

V: Standardhälve on arv, mida kasutatakse selleks, et öelda, kuidas mingi rühma mõõtmistulemused on keskmisest (keskmisest või oodatavast väärtusest) laiali.

K: Mida tähendab madal standardhälve?

V: Madal standardhälve tähendab, et enamik numbreid on keskmisele lähedal.

K: Mida tähendab suur standardhälve?

V: Suur standardhälve tähendab, et arvud on rohkem hajutatud.

K: Kuidas kasutatakse standardhälvet rahas?

V: Rahas näitab teenitud intresside standardhälve, kui palju ühe inimese teenitud intressid võivad erineda keskmisest.

K: Millal saab mõõta ainult osa rühmast?

V: Paljudel juhtudel saab mõõta ainult valimit või osa rühmast.

K: Kuidas esitatakse kogu rühma standardhälve?

V: Kogu rühma standardhälvet kujutatakse kreeka tähega َ \displaystyle \sigma }. .

K: Kuidas esitatakse valimi standardhälvet?

V: Valimi standardhälvet tähistab s {\displaystyle s} .