Heisenbergi määramatuse printsiip

Diagrammid

6. See animatsioon näitab universumi määramatuse olemuse üht olulist tagajärge: elektronide kvant-tunneldamist. Vaadake tähelepanelikult. Iga kord pääseb natuke läbi barjääri.


5. Keskmise vahe vedruga ülesriputamine võimaldab mõõta impulssi, kuid see liigutab vahe ettearvamatult, nii et teave iga fotoni asukoha kohta keskel läheb kaduma.


4. Väikese auguga tõkke külge paigaldatud vedru paneb osakese läbi augu suruma, mis surub tõkke, venitab vedru ja mõõdab nii hoogu. Kuid kuna vedruga paigaldatud tõkkepuu liigub, ei ole me nii kindlad selles, kus osakeste asukoht oli, kui nad läbi augu läksid, ning difraktsioon mõjutab ka nende asukohta avastamisekraanil.


3. Auku ahenemine suurendab kindlust, kus fotoon keskel on, kuid siis muutub selle suund sealt paremal asuvale avastamisekraanile vastavalt ebakindlamaks. Fookus muutub häguseks. Auku laiendades jõuavad kõik fotoonid avastamisekraani keskele, kuid siis on meil vähem aimu, kus nad olid, kui nad keskmisest tõkkest läbi läksid.


2. Auku ahenemine painutab osakeste teed augu servade ümber (difraktsioon), nii et saadav kiir muutub suuremaks ja pehmemaks.


1. Fotoonid, elektronid ja muud subatomaarsed osakesed jõuavad suurest august läbi tulistatuna teravasse fookusesse, kuid me ei tea täpselt, kus nad keskmisel teel olid.

Kuidas inimesed õppisid ebakindlust tundma?

Väga varsti pärast seda, kui Werner Heisenberg lõi uue kvantfüüsika, tuli otse tema matemaatikast välja midagi ootamatut, väljend:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }\qquad \qquad \qquad \qquad }

Positsioonivea (x) korrutatuna impulsi (p) vea vahemikuga on umbes võrdne või suurem kui Plancki konstant jagatud 4π-ga.

Need sümbolid panevad matemaatiliselt kirja selle, mida te juba nägite ülaltoodud piltidel. Sümbolid ütlevad selgelt, et te ei saa olla täiesti kindel, kus miski on ja kuhu see läheb. Kui te saate selgemalt aru, kus see igal ajal on, siis on teil vähem aimu, kuhu ja kui kiiresti see liigub. Kui te saate igal ajal selgemaks, kuhu see läheb ja kui kiiresti, siis on teil vähem ettekujutust sellest, kus see praegu on.

Teadlased olid juba teada saanud, miks teatavad ained annavad kuumutamisel või muul viisil ergastamisel iseloomulikke valgusvärve. Heisenberg püüdis seletada, miks neil värvidel on iseloomulik heledus. Sellest ei oleks piisanud, kui ta ja teised teadlased oleksid lihtsalt öelnud: "Noh, see on lihtsalt nii". Nad olid kindlad, et nendele erinevustele ja sellele, et heledate joonte tugevuste vahekord oli iga elemendi proovi puhul alati ühesugune, pidi olema hea põhjus.

Tal polnud aimugi, et ta komistab looduse varjatud saladuse otsa, kui ta asus avastama igale elemendile iseloomulike värviliste joonte intensiivsuse seletust. Kvantmehaanika uurimine oli juba näidanud, miks vesinikul on neli heledat joont selles spektriosas, mida inimesed näevad. Ilmselt tundus, et järgmine asi, mida tuli õppida, on lihtsalt see, kuidas nende heledust arvutada. Vesinik tundus olevat ilmselge koht, kust alustada, sest vesinikul on ainult üks elektron, millega tuleb toime tulla, ja ainult neli joont spektri nähtavas osas. Kindlasti peab olema hea põhjus, miks need ei ole võrdselt heledad. Seletus neooni ja teiste elementide erivärviliste joonte heledusele võis oodata.

 

Heisenberg alustas tööd kvantfüüsikaga, kohandades klassikalisi elektrienergia võrrandeid, mis on algselt väga keerulised, nii et tema 1925. aasta töö matemaatikat oli väga raske jälgida.

Ta püüdis leida õiget viisi, kuidas arvutada heledate joonte intensiivsust vesiniklampide spektris. Ta pidi leidma seotud suuruse nimega "amplituud" ja korrutama amplituudi amplituudiga (ehk teisisõnu pidi ta amplituudi ruudutama), et saada soovitud intensiivsus. Ta pidi välja mõtlema, kuidas väljendada amplituudi viisil, mis võtaks arvesse asjaolu, et vesiniklambid ei kiirga kõikidel sagedustel ja ei kiirga spektri inimeste poolt nähtava spektriosa pidevas sagedusalas. Heisenberg leidis märkimisväärse uue viisi amplituudi arvutamiseks.

Kummaline võrrand|võrrand, mille Heisenberg avastas ja mida ta kasutas ühe kvantkoguse (nt positsioon) korrutamiseks teise kvantkogusega (nt impulss), avaldati 1925. aasta juulis avaldatud "Heisenbergi "maagilises" dokumendis" (Heisenberg's 'magic' paper of July 1925).

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

Ülaltoodud matemaatika tundub väga raske, kuid sellele eelnev matemaatika on palju raskem ja seda on äärmiselt raske mõista. See on siin toodud lihtsalt selleks, et näidata, kuidas see välja nägi. Heisenbergi töö on ajalooline verstapost. Paljud füüsikud, kes lugesid tema tööd, ütlesid, et nad ei saa tema järeldustega mitte nõustuda, kuid nad ei suutnud jälgida tema selgitusi, kuidas ta nende järeldusteni jõudis. Heisenbergi kasutatud algvõrrandid hõlmasid Fourier' jadasid, milles oli palju tegureid. Me tuleme tagasi ülaltoodud võrrandi juurde, sest see on omamoodi retsept maatriksite välja kirjutamiseks ja korrutamiseks.

Uued võrrandid pidid olema nii kummalised ja ebatavalised, sest Heisenberg kirjeldas kummalist maailma, kus mõned asjad, näiteks elektronide orbiidid, ei muutu aeglaselt suuremaks ega väiksemaks. Uut tüüpi muutused hõlmavad hüppeid ja suuri vahed hüpetevahelisi lünki. Elektronid saavad hüpata ainult teatud orbiitide vahel ning orbiitide vahelisel muutumisel saadud või kaotatud energia tekib siis, kui neeldub õige energiaga footon või tekib uus õige energiaga footon. Kui vesiniku aatomi elektronid hüppavad kõige sagedamini kahe konkreetse orbiidi vahel alla (langevad), siis emiteeritakse sellel energiatasemel rohkem footoneid ja seega on sellel tasemel tekkiv valgus kõige intensiivsem.

Raske oli panna pidevate spektrite (mida näete, kui panete päikesevalguse läbi prisma) jaoks loodud võrrandeid sobima spektritega, millel on vaid mõned tippsagedused, mille vahel ei ole midagi. Peaaegu kõik, mida oli juba valguse ja energia kohta teada saadud, oli tehtud suurte asjadega, nagu põlevad küünlad või päike, ja need suured objektid annavad kõik pidevaid spektreid. Kuigi nende tavalise suurusega asjadega oli lihtne eksperimente teha, oli ikkagi kulunud palju aega, et välja selgitada neid reguleerivaid (füüsika)seadusi. Nüüd tegelesid füüsikud liiga väikeste asjadega, mis ei tekitanud pidevaid spektreid, ja püüdsid leida viisi, kuidas saada vähemalt vihjeid sellest, mida nad juba teadsid, mis aitaks neil leida nende väikeste ja hajusate valgusallikate seadusi.

Esialgsed võrrandid käsitlesid mingisugust vibreerivat keha, mis tekitaks laine, natuke nii nagu orelil olev pillikeel tekitab iseloomuliku sagedusega helilaine. Seega oli liikumine edasi-tagasi (nagu pilliroo võnkumine) ja tekkis kiiratav laine, mida võis graafiliselt kujutada siinuslainena. Suur osa sellest, mida varem oli füüsika kohta aatomi tasandil välja selgitatud, oli seotud elektronide liikumisega tuumade ümber. Kui mass liigub orbiidil, kui ta pöörleb ümber mingi keskme, siis on tal nn "nurkamoment". Nurkliikumism on see, kuidas midagi sellist nagu karussell jätkab pöörlemist pärast seda, kui inimesed on lõpetanud selle lükkamise. Matemaatika, mida kasutatakse faaside ja nurkmomendi arvutamiseks, on keeruline. Pealegi ei näidanud Heisenberg oma 1925. aasta töös kõiki oma arvutusi, nii et isegi headel matemaatikutel võib olla raskusi selle täitmisega, mida ta ei öelnud.

Kuigi paljud füüsikud ütlesid, et nad ei suutnud välja mõelda erinevaid matemaatilisi samme Heisenbergi läbimurdelises töös, kasutab üks hiljutine artikkel, mis püüab selgitada, kuidas Heisenberg oma tulemuseni jõudis, kakskümmend matemaatikaga täidetud lehekülge. Isegi sellest artiklist ei ole lihtne aru saada. Matemaatika algas väga rasketest asjadest ja lõpuks annaks tulemuseks midagi suhteliselt lihtsat, mis on näidatud selle artikli ülaosas. Lihtsama tulemuse saamine ei olnud lihtne, ja me ei püüa näidata protsessi, kuidas jõuda iganenud universumi pildilt uue kvantfüüsikani. Meil on vaja vaid piisavalt üksikasju, et näidata, et peaaegu kohe, kui Heisenberg tegi oma läbimurde, tuli nähtavale osa universumi toimimisest, mida keegi varem ei olnud näinud.

Heisenberg pidi olema väga põnevil, kuid ka väga väsinud, kui ta hilisõhtul lõpuks oma läbimurde tegi ja hakkas endale tõestama, et see töötab. Peaaegu kohe märkas ta midagi kummalist, midagi, mida ta pidas tüütuks väikeseks probleemiks, mille ta võiks kuidagi kõrvaldada. Kuid selgus, et see väike häda oli suur avastus.

Heisenberg oli töötanud amplituudi korrutamise suunas amplituudiga ja nüüd oli Heisenbergil hea viis amplituudi väljendamiseks, kasutades oma uut võrrandit. Loomulikult mõtles ta korrutamisele ja sellele, kuidas ta korrutaks asju, mis olid antud keeruliste võrrandite abil.

Heisenberg mõistis, et lisaks amplituudi ruutkeskmisele tahab ta lõpuks korrutada positsiooni impulsiga või korrutada energiat ajaga, ja tundus, et neil uutel juhtudel oleks vahet, kui ta pööraks järjekorra ümber. Heisenberg arvas, et ei peaks olema oluline, kas korrutada positsiooni impulsiga või korrutada impulsi positsiooniga. Kui need oleksid olnud vaid lihtsad arvud, poleks olnud mingit probleemi. Kuid need olid mõlemad keerulised võrrandid ja see, kuidas sa said arvud võrranditesse sisestada, osutus erinevaks sõltuvalt sellest, kummal viisil sa alustasid. Looduses tuli mõõta asukohta ja seejärel mõõta impulssi või siis mõõta impulssi ja seejärel asukohta, ja matemaatikas valitses sama üldine olukord. (Vaata ingliskeelset Vikipeedia artiklit Heisenbergi sissekäik maatriksmehaanikasse, kui tahad teada saada keerulisi üksikasju!) Pisikesed, kuid tüütud erinevused tulemuste vahel pidid jääma, ükskõik kui väga Heisenberg ka ei soovinud, et need kaduma läheksid.

Sel ajal ei saanud Heisenberg sellest ühest väikesest probleemist lahti, kuid ta oli kurnatud, nii et ta andis oma töö oma otsesele ülemusele Max Bornile üle ja läks puhkusele.

Max Born oli tähelepanuväärne matemaatik, kes peagi nägi, et Heisenbergi antud võrrand oli omamoodi retsept maatriksi kirjutamiseks. Dr. Born oli tol ajal üks väheseid inimesi, kes huvitus sellest kummalisest matemaatikast, millest enamik inimesi arvas, et see ei ole eriti hea. Ta teadis, et maatriksid saab korrutada, nii et kõiki arvutusi ühe füüsikaprobleemi arvestamiseks saab teha ühe maatriksi korrutamisega teise maatriksiga. Lihtsalt võime panna keerulise protseduuri standardsesse ja vastuvõetavasse vormi, muudaks selle töö lihtsamaks. See võiks muuta selle ka teiste inimeste jaoks kergemini vastuvõetavaks.

Born oli nii hea matemaatik, et ta sai peaaegu kohe aru, et kahe maatriksi korrutamise järjekorra muutmine annab erineva tulemuse, ja tulemused erineksid väikese summa võrra. See summa oleks h/2πi. Igapäevaelus oleks see erinevus nii väike, et me isegi ei näeks seda.

Kaks lainet, mis ei ole omavahel faasis.


Päikese täielik visuaalne spekter. Puuduvad lüngad. See diagramm näitab intensiivsusi erinevatel sagedustel.


Neoon spektrile


Vesiniku spekter


Teatud molekulide ergastamisel annavad nad iseloomulikku värvi.

Formaalse määramatuse teooria juurde

See võttis paar aastat aega, kuid Heisenberg suutis tõestada määramatuse printsiibi, mis ütleb, et Δx × Δp = h/2, mis on arv, mis tuleb välja algsetest võrranditest, kuid jätab välja π ja i, mis on seotud faasimuutustega. Heisenberg selgitas, et ta tuletas oma määramatuse printsiibi sellest varasemast tulemusest, kui ta 1927. aastal kirjutas seda teooriat tutvustava artikli.

Konstant, mida kirjutatakse h, mida nimetatakse Plancki konstandiks, on salapärane arv, mis esineb sageli, nii et me peame mõistma, mis see pisike arv on. Numbriliselt on see tavaliselt antud kui 6,62607×10^-34 J s (džauli sekundit). Seega on see suurus, mis hõlmab energiat ja aega.

See avastati, kui Planck mõistis, et täiusliku kiirguse (mida nimetatakse musta keha kiirguseks) energia kiiratakse kindla suurusega ühikutes, mida nimetatakse "kvantideks" (selle sõna ainsuses on "kvant"). Välja kiiratud energia kiiratakse footonitena ja footoni sagedus on proportsionaalne tema poolt antud "löögi" suurusega. Me kogeme nähtava valguse erinevaid sagedusi erinevate värvidena. Spektri violetses otsas on igal fotonil suhteliselt suur energiakogus; spektri punases otsas on igal fotonil suhteliselt väike energiakogus. Fotoni energia hulga arvutamise viisiks on võrrand E = hν (energia võrdub Plancki konstandiga korda "nu" ehk sagedusega).

Heisenbergi määramatuse printsiip Δx × Δp ≥ h ütleb meile, et kui me püüame teatud arvupaaridele kindlaks teha, saame ainult nii lähedale, ja et kui me püüame ühele neist täpsemalt vastata, st kui me püüame Δx väiksemaks teha, et meil oleks parem ettekujutus millegi asukohast, siis peame saama tagasi suurema arvu selle paari teise arvu jaoks, ja et summa, mille võrra need kaks erinevad, on tihedalt seotud h-ga.

Teine füüsikaliste suuruste paar käib vastavalt määramatuse seosele: ΔE × Δt ≥ h, ja see paar näitab muu hulgas, et kui me vaatame tähtedevahelisse ruumi, mõnda kohta, kus me ei ootaks üldse midagi leida, ja vähendame Δt üha lähemale ja lähemale 0-le, siis võrrandis näidatud tasakaalu säilitamiseks peab ΔE muutuma üha suuremaks - ja äkki võib midagi, millel on hoogu, just selleks lühikeseks ajaks tekkida.

Kuidas seletada seda määramatust (kindluse puudumist)? Mis toimub Universumis? Sageli öeldakse, et uus teooria, mis on edukas, võib anda uut teavet uuritavate nähtuste kohta. Heisenberg lõi matemaatilise mudeli, mis ennustas õigeid intensiivsusi vesiniku heledate joonte spektrile, kuid kavatsemata avastas ta, et teatud füüsikaliste suuruste paarid avaldavad ootamatut määramatust. Kuni selle hetkeni ei olnud kellelgi aimu, et mõõtmisi ei saa igavesti üha täpsemaks ja täpsemaks muuta. Asjaolu, et neid ei saa teha kindlamaks, kindlamaks, oli hämmastav uus avastus. Paljud inimesed ei tahtnud seda aktsepteerida.

Bohr ja tema kolleegid väitsid, et fotoonidel, elektronidel jne ei ole enne mõõtmist ei asukohta ega impulssi. See teoreetiline seisukoht kasvas välja määramatuse avastamisest ja ei olnud lihtsalt mingi isiklik eelistus selle kohta, mida uskuda. Bohr ütles, et me ei tea midagi, näiteks fotoni või elektroni kohta, enne kui me seda vaatleme. Selleks, et sellist väikest asja jälgida, peame sellega kuidagi suhtlema. Igapäevaelus on võimalik teha midagi sellist, nagu kõndida auto kõrval, märkides samal ajal üles, kui see läbib punkte kõnniteele joonistatud ruudustikus. Võib-olla vajutab auto enda kaal kõnniteel olevaid väikeseid hoobasid, mis lülitavad välja igaühe külge kinnitatud kellad ja registreerivad auto kaalu. Lõpuks oleks meil selge ülevaade sellest, kus auto eri aegadel oli, ning samuti saaksime arvutada selle liikumissuuna ja kaalu. Siis saaksime igal kellaaegadel teada nii auto asukohta kui ka tema impulssi (kiirus korrutatud massiga). Me ei kujutaks isegi ette, et väikeste hoobade liigutamiseks vajalik jõud mõjutaks mingil moel auto liikumist. Samuti ei kujutaksime ette, et autol ei oleks asukohta ega trajektoori nende punktide vahel kõnniteel, kus on hoovad, või et auto eksisteerib nende aegade jooksul mingis kolmemõõtmelises hägususes ja rahuneb ainult siis, kui ta vajutab hooba. Meile tuttav maailm ei näita selliseid kummalisi vastastikmõjusid.

Pimedal ööl merel asuva laeva asukoha määramiseks võiksime kasutada otsingulampi ja see valgus ei häiriks laeva asukohta ega liikumissuunda, kuid elektroni asukoha määramiseks valguse abil oleks vaja tabada seda ühe või mitme footoniga, millel on piisavalt hoogu, et häirida elektroni asukohta ja liikumissuunda. Elektroni leidmine muude vahenditega eeldaks selle hoidmist mingisuguse füüsilise piirangu all, mis samuti lõpetaks selle edasiliikumise.

Fotoni asukoha määramiseks on parim, mida saab teha ilma selle edasiliikumist lõpetamata, see, et see läbib ringikujulise augu tõkkes. Kui on teada aeg, mil fotoon kiirgas (näiteks laseriga) ja aeg, mil fotoon jõuab avastamisekraanile, näiteks digitaalkaamerale, siis on võimalik arvutada aeg, mis kulus selle vahemaa läbimiseks, ja aeg, mil fotoon läbis augu. Selleks, et foton saaks sellest läbi minna, peab ümmarguse augu läbimõõt olema siiski suurem kui fotoni suurus. Mida väiksem on ringikujuline auk, seda lähemale jõuame fotoni täpse asukoha teadasaamisele selle läbimisel. Siiski ei saa me kunagi teada, kas foton on sel ajal keskpunktist väljas. Kui auk on täpselt sama suur kui foton, siis ei lähe see läbi. Kui augu läbimõõt väheneb, muutub fotoni impulss või suund august väljumisel üha enam ja enam.

Niels Bohr ja tema kolleegid väitsid, et me satume suurtesse raskustesse, kui eeldame, et asjad, mis on liiga väikesed, et neid isegi mikroskoobiga näha, on tõesed, mille kohta meil on tõendeid ainult igapäevaelu skaalal. Igapäevaelus on asjadel alati kindel asukoht. Aatomi skaalal ei ole meil mingeid tõendeid, mis seda järeldust toetaksid. Igapäevaelus on asjadel kindel aeg, millal nad toimuvad. Aatomi skaalal ei ole meil mingeid tõendeid, mis toetaksid seda järeldust. Kui igapäevaelus vaadeldakse tehast esimese päeva öisest vahetusest teise päeva päevavahetuseni ja vaadatakse, kuidas valmis auto veodokki veetakse, siis poleks mõtet öelda, et on võimatu öelda, kas see on tarnitud öise vahetuse või päevase vahetuse ajal. Kuid aatomi skaalal saame näidata juhtumeid, kus me peame arvestama, et üks foton on toodetud kahel ajal. (Kui see ei ole piisavalt halb, siis võime näidata ka juhtumeid, kus üks foton on toodetud kahest kõrvuti asetsevast laserist).

Aatomi skaalal toimuva väljaselgitamisel on osaliselt raskusi selles, et me tahaksime teada nii seda, kus miski on, kui ka seda, milline on selle liikumistee, ning teada mõlemat asja üheaegselt, kuid me ei saa mõõta nii asukohta kui ka liikumisteed üheaegselt. Me kas mõõdame fotoni või elektroni impulsi ühel hetkel ja seejärel mõõdame ilma suurema viivituseta kui vaja selle asukohta või me vahetame asju ümber ja mõõdame kõigepealt asukohta ja seejärel impulsi. Probleem seisneb selles, et kui teeme esimese mõõtmise üsna kindlal kujul (surudes seda kuidagi maha), siis suurendame järgmise mõõtmisega seotud määramatust. Kui meie esialgsed mõõtmised oleksid nii jämedad, et igaühe puhul tekiks palju vigu, siis saaksime asju parandada, kasutades igaühe tegemiseks kergemat puudutust, kuid me ei saaks kunagi üle teatud täpsuspiiri.

Me teame igapäevaelust, et kui proovime kaaluda midagi vannitoakaalul, mis on asetatud pesumasinasse tsentrifuugimisse, siis saame ebatäpseid tulemusi, sest kaalule asetatud nõel hakkab halvasti vibreerima. Me võime pesumasina välja lülitada. Väga täpsete mõõtmiste tegemiseks leiame aga, et naabruses mööduvad veoautod panevad nõela kõikuma, nii et võime panna kaalu millegi peale, et seda välisest häirest isoleerida. Usume, et suudame vibratsioonid piisavalt kõrvaldada, et saada just nii täpseid tulemusi, kui me tahame. Me ei mõtle kunagi sellele, et asi skaalal ise vibreerib või et tal on määramata impulss.

Kui lähtuda ebamäärasuse printsiibist, siis tundub, et tegelikult ei ole ühegi aatomi mõõtkavas oleva asja jaoks kindlat asendit ega kindlat impulssi ning et eksperimenteerijad saavad asju sundida kindlusesse ainult ebamäärasuse printsiibis sätestatud piirides. Bohr ja tema kolleegid väitsid ainult, et me ei saa midagi teada ilma mõõtmisi tegemata, ja kui mõõtmised on tehtud, siis saame asju suruda kindlama asendi või kindlama impulsi suunas, kuid et me ei saa absoluutset kindluse või määramatuse printsiipi, mida me tahaksime. Teised aga võtsid seda võimalust tõsiselt ja väitsid, et kui matemaatika on õige, siis ei saa üliväikeste maailmas olla kindlus või kindlus. Teaduse olemus seisneb selles, et matemaatika on ainult tegelikkuse mudel ja ei ole mingit garantiid, et see on õige mudel.

Matemaatika ja matemaatikaga ennustatud asjade praktilised tagajärjed on nii usaldusväärsed, et nendega on väga raske mitte nõustuda, kuid see, mida matemaatika ütleb tegeliku maailma kohta, on tekitanud mitmeid erinevaid ideid. Niels Bohri juures Kopenhaagenis töötanud teadlaste seas peeti määramatuse printsiipi nii, et elementaarsel tasandil ei eksisteeri füüsikaline universum deterministlikul kujul. Pigem on see tõenäosuste või potentsiaalide kogum.

Vastukaaluks Kopenhaageni grupi poolt matemaatikaga seotud loole on ka teisi lugusid, nagu näiteks "mitme universumi tõlgendus", mis ütleb, et iga kord, kui kvantteooria kohaselt on mitu võimalikku tulemust, toimub iga tulemus omaette uues universumis. Einstein väitis, et mitut võimalikku tulemust ei ole, seega on ainult üks universum ja see on determinatiivne, või nagu ta ütles: "Jumal ei mängi täringut".

Kui h oleks väikseim võimalik energiakogus, siis ei oleks eri sagedusega footonites sisalduvat energiat näitav põhivõrrand tasakaalus. See oleks vale.

Vastuväited määramatuse printsiibi vastu

Albert Einstein nägi, et uus kvantmehaanika eeldab asukoha ja impulsi puudumist mõõtmistele eelnevas ajas, ja ta oli selle vastu. Ta uskus kindlalt, et asjadel olid enne mõõtmist kindlad asendid ja kindlad impulsid ning et asjaolu, et paari asja ühe mõõtmine ja teise täpse mõõtmise võimaluse häirimine ei räägi selle poolt, et kumbki neist puudus enne mõõtmist. Ta ja kaks tema kolleegi kirjutasid selle, mis on saanud tuntuks kui "EPR-paber". Selles paberis väidetakse, et peavad olema omadused, mis määravad positsiooni ja impulsi, ja et kui me suudame neid näha või kui me saame nende kohta teavet, siis saame matemaatiliselt teada ja ennustada positsiooni ja impulsi. Pikka aega arvasid inimesed, et ei ole võimalik tõestada või ümber lükata seda, mis oli Einsteini jaoks usutunnistus. See vaidlus oli väga viljakas, sest see viis kõigi kaasaegsete arenguteni põimumise vallas.

Matemaatiliselt on Einstein tõestanud, et ta on eksinud. 1964. aastal töötas John Stewart Bell välja matemaatilise meetodi, et eristada kahe osakese käitumist, mille olekud on kindlad, kuid mis on lihtsalt teadmata kahele neid uurivale isikule, ja kahe osakese käitumist, mille olekud on põimunud, kuid mis on määramata või ebakindlad, kuni neid ei mõõdeta. Tema meetod näitab, et tõenäosused teatud tulemuste saamiseks on kahe erineva eelduse korral erinevad. Tema tööd nimetatakse Belli teoreemiks või Belli ebavõrdsuseks. Katsed on näidanud, et loodus käitub nii, nagu Bell seda kirjeldab.

Teine tee ebakindlusele

Heisenbergi määramatuse printsiibi algsed arutelud sõltusid mudelist, mis ei arvestanud, et aineosakestel, nagu elektronid, prootonid jne, on lainepikkus. 1926. aastal näitas Louis de Broglie, et kõigil asjadel, mitte ainult footonitel, on oma sagedus. Asjadel on lainepõhine ja osakestepõhine olemus, nagu ka fotoonidel. Kui me püüame teha sellise asja nagu prooton laine kitsamaks ja kõrgemaks, siis muutuks selle asukoht selgemaks, kuid siis muutuks impulss ebaselgemaks. Kui me püüame laine kirjelduse impulsiosa selgemaks muuta, st panna see jääma kitsamasse väärtusvahemikku, siis laine tipp hajub laiali ja selle asukoht muutub ebaselgemaks.

Laine, mis on osa fotoni kirjeldusest, ei ole kvantmehaanikas samasugune asi nagu laine ookeani pinnal või kokkusurutud õhu ja hõreda õhu piirkonnad, mis moodustavad helilained. Selle asemel on nendel lainetel tipud või suure amplituudiga piirkonnad, mis on seotud tõenäosusega, et selles punktis ruumis ja ajas midagi leidub. Täpsemalt öeldes on see amplituudi ruut, mis annab tõenäosuse, et mingi nähtus ilmneb.

Fotoni suhtes kohaldatav laine võib olla puhas siinuslaine. Sellisel juhul annaks iga piigi väärtuse ruut selle punkti fotoni vaatlemise tõenäosuse. Kuna siinuslainete amplituudid on kõikjal ühesugused, oleks fotoni leidmise tõenäosus igas punktis sama. Seega praktiliselt võttes ei annaks laine teadmine ühe sellise fotoni jaoks vihjet, kust seda otsida. Teisest küljest on fotoni impulss matemaatiliselt seotud selle laine amplituudiga. Kuna antud juhul on tegemist puhta siinuslainega, siis on laine iga tsükli amplituud sama ja seega on selle lainega seotud ainult üks impulsi väärtus. Me ei teaksime, kuhu fotoon tabab, kuid me teaksime täpselt, kui tugevalt ta tabab.

Valguskiirte puhul, mis fookustuvad mingisse punkti avastuskraanil, ei ole fotoonidega seotud lained puhtad siinuslained. Selle asemel on tegemist lainetega, millel on suur amplituud ühes punktis ja palju väiksemad amplituudid mõlemal pool seda kõrgeimat tippu. Matemaatiliselt on võimalik analüüsida sellist lainet mitmeks erineva lainepikkusega sinuslaineks. Veidi lihtsam on visualiseerida selle protsessi tagasipöördumist, vaadeldes ühe sagedusega esialgset siinuslainet, millele lisatakse teine erineva lainepikkusega siinuslaine, seejärel kolmas, seejärel neljas jne. Tulemuseks on komplekslaine, millel on üks kõrge tipp ja mis sisaldab suurt hulka erineva lainepikkusega ja seega erineva impulssiga laineid. Sellisel juhul on tõenäosus, et fotoon ilmub teatud punktis, äärmiselt suur, kuid tema poolt edastatav impulss võib osutuda seotuks mis tahes komponendilainete lainepikkusega. Teisisõnu, väärtus p = ħ/λ ei ole enam ühtne väärtus, sest arvesse tuleb võtta kõiki kokku pandud "erineva lainepikkusega lainete" pikkusi.

Simulatsioon näitab, kuidas matemaatiliselt modelleerida osakese asukoha teravdamist: Asetage mitu erinevat lainekuju üle algse siinuslaine. Keskpunktist moodustub üha kõrgem ja kõrgem tipp, ülejäänud tippude arv suureneb, kuid nende kõrgus väheneb, sest nad segunevad üksteisega. Nii et lõpuks on superpositsioonis palju erinevaid laineid, millest igaühel on erinev lainepikkus ja (p = ħ/λ järgi) erinev impulss, kuid ainult üks väga kõrge tipp, mis kasvab kõrgemaks ja kitsamaks ning annab meile midagi, mis on üha lähemal ja lähemal kindlale positsioonile.

Selleks, et muuta hoogu üha kindlamaks, peaksime üha rohkem ja rohkem üksteise peale pandud siinuslaineid ära võtma, kuni järele jääb ainult lihtne siinuslaine. Seejuures vähendaksime järk-järgult keskse tipu kõrgust ja suurendaksime järk-järgult konkureerivate kohtade kõrgust, kus võib leida osakese.

Seega, kui me alustame subatomaarsete osakeste lainepildiga, siis tavaliselt on meil alati tegemist suhteliselt kõrgete keskmiste tippude ja suhteliselt paljude komponentide lainepikkustega juhtumitega. Sellistes tingimustes ei saa kunagi ennustada täpset asukohta või täpset impulssi. Kui matemaatiline mudel on tegeliku maailma täpne kujutis, siis ei ole ühelgi footonil või muul subatomaarsel osakestel ei täpset asukohta ega kindlat impulssi. Kui me mõõdame sellist osakest, võime valida meetodi, mis pigistab piiki veelgi ja muudab selle kitsamaks, või võime valida meetodi, mis langetab piiki ja tasandab komponentide lainepikkused. Sõltuvalt sellest, mida me mõõdame ja kuidas me seda mõõdame, võime muuta oma asukoha kindlamaks või kitsamaks impulsside vahemikku. Me võime katse kavandamisel olla ettevaatlikud, et vältida erinevaid võimalusi aparaadi raputamiseks, kuid me ei saa vabaneda sellest, et alguses ei olnud midagi täiesti kindlat.

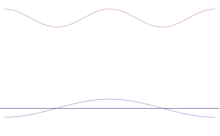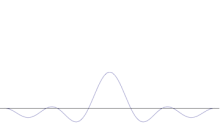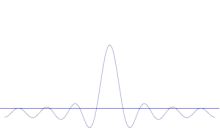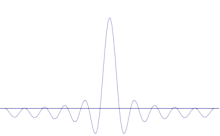
Mitme tasapinnalise laine superpositsioon. Lainepakett muutub paljude lainete lisandumisel üha enam lokaliseerituks. Fourier' teisendus on matemaatiline operatsioon, mis lahutab lainepaketi üksikuteks tasalaineteks. Pange tähele, et siin näidatud lained on ainult illustratiivsetel eesmärkidel reaalne, samas kui kvantmehaanikas on lainefunktsioon üldiselt kompleksne.

Kultuurilised mõjud

Heisenbergi määramatuse printsiibi tähtsaim mõju on olnud tahtevabadust käsitlevatele argumentidele. Klassikalise füüsika teooriate alusel on võimalik väita, et põhjuse ja tagajärje seadused on paratamatud ja et kui universum algas teatud viisil, siis on võimalik sellest algseisundist lähtuvalt arvutada kogu tulevikus toimuva aine ja energia vastastikmõju. Kuna kõik on absoluutselt selle tulemus, mis oli enne seda, siis on iga otsus, mille inimene teeb, ja iga olukord, millesse ta satub, aegade algusest peale ette määratud. Meil ei ole siis mingit valikut selles, mida me teeme.

Tahtevabadusse usuvad inimesed väidavad, et kvantmehaanika seadused ei ennusta, mis juhtub, vaid ainult seda, mis on rohkem ja mis vähem tõenäoline. Seetõttu on iga tegevus juhuslike "mündiheitluste" seeria tulemus ja ühtegi otsust ei saa tagasi viia vajalike eeltingimuste kogumile.

Väljendid "kvanthüpe" ja "kvanthüpe" on muutunud tavaliseks viisiks, kuidas asjadest rääkida. Tavaliselt kavatsetakse kirjeldada midagi, mis hõlmab tohutut muutust, mis toimub lühikese aja jooksul. Tegelikult kasutatakse seda terminit selle kohta, kuidas elektron käitub aatomis, kui ta neelab väljastpoolt tulevat fotooni ja hüppab seega ühelt orbiidilt ümber aatomituuma kõrgemale orbiidile või kui ta kiirgab fotooni ja langeb seega kõrgemalt orbiidilt madalamale orbiidile. Neils Bohri ja tema kolleegide idee oli, et elektron ei liigu orbiitide vahel, vaid kaob ühelt orbiidilt ja ilmub koheselt teisele orbiidile. Nii et kvanthüpe ei ole tegelikult mingi maad purustav muutus, vaid äkiline väike muutus ühest valdkonnast teise.

Kui inimene mõõdab mingit protsessi subatomaalsel skaalal ja määramatuse põhimõte avaldub, siis võib öelda, et inimese tegevus on mõjutanud mõõdetavat asja. Mõõtmise tegemine, mille eesmärk on saada kindlaid andmeid osakese asukoha kohta, mõjutab paratamatult tema impulssi ja mida iganes tehakse, et mõõta seda impulssi võimalikult kiiresti pärast asukoha mõõtmist, ei saa jätta muutmata tõenäosust, milline impulss avastatakse. Seega saab määramatuse printsiibiga seletada mõningaid uurijate poolt tekitatud häireid, mis mõjutavad eksperimendi või vaatluse tulemusi. Siiski ei ole kõik vaatleja mõjud tingitud kvantmõjudest või määramatuse printsiibist. Ülejäänud on "vaatlejaefektid", kuid mitte kvantmääramatuse efektid.

Vaatleja mõju hõlmab igasuguseid asju, mis toimivad meie tavalises inimlikus skaalas. Kui antropoloog püüab saada selget ettekujutust elust primitiivses ühiskonnas, kuid tema kohalolek ärritab kogukonda, mida ta külastab, siis võivad tehtud tähelepanekud olla väga eksitavad. Siiski ei toimu ükski asjakohane vastastikmõju kvantmehaanika või määramatuse printsiibi poolt kirjeldatud tasandil.

Mõnikord kasutatakse sõna "kvant" reklaami eesmärgil, et näidata midagi uut ja võimsat. Näiteks väikeste bensiinimootorite tootjal Briggs ja Strattonil on üks rida neljasilindrilisi väikese hobujõuga mootoreid bensiinimootoriga niidukitele ja sarnastele aiatööriistadele, mida ta nimetab "Quantum".

Rohkem lugemist

• Introducing Quantum Theory, lk 115 ja lk 158.

J.P. McEvoy ja Oscar Zarate