Plancki konstant

Taust

Käesolevas artiklis kasutatud sümbolid.
Sümbol Tähendus E Energia h Plancki konstant k Boltzmanni konstant c valguse kiirus λ kiirguse lainepikkus ν kiirgussagedus T absoluutne temperatuur

Aastatel 1670-1900 arutasid teadlased valguse olemust. Mõned teadlased uskusid, et valgus koosneb paljudest miljonitest pisikestest osakestest. Teised teadlased uskusid, et valgus on laine.

Valgus: lained või osakesed?

1678. aastal kirjutas Christiaan Huygens raamatu "Traité de la lumiere" ("Traktaat valguse kohta"). Ta uskus, et valgus koosneb lainetest. Ta väitis, et valgus ei saa koosneda osakestest, sest kahe valgusvihu valgus ei põrku teineteisest tagasi. 1672. aastal kirjutas Isaac Newton raamatu "Opticks". Ta uskus, et valgus koosneb punastest, kollastest ja sinistest osakestest, mida ta nimetas korpusteks. Newton selgitas seda oma "kahe prisma katsega". Esimene prisma lõhkus valguse eri värvideks. Teine prisma ühendas need värvid tagasi valgeks valguseks.

18. sajandil pöörati kõige rohkem tähelepanu Newtoni teooriale. Aastal 1803 kirjeldas Thomas Young "topeltlõike eksperimenti". Selles katses segab valgus, mis läbib kaks kitsast pilu, iseennast. See põhjustab mustri, mis näitab, et valgus koosneb lainetest. Kogu ülejäänud XIX sajandi jooksul pöörati valguse laineteooriale kõige rohkem tähelepanu. 1860. aastatel töötas James Clerk Maxwell välja võrrandid, mis kirjeldasid elektromagnetilist kiirgust kui laineid.

Elektromagnetilise kiirguse teooria käsitleb valgust, raadiolainete, mikrolaineid ja paljusid teisi laineid ühe ja sama asjana, välja arvatud, et neil on erinevad lainepikkused. Valguse lainepikkus, mida me oma silmadega näeme, on ligikaudu 400 ja 600 nm vahel. Raadiolainete lainepikkus varieerub 10 m kuni 1500 m ja mikrolainete lainepikkus on umbes 2 cm. Vaakumis liiguvad kõik elektromagnetlained valguse kiirusega. Elektromagnetlaine sagedus on antud järgmiselt:

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}.

Sümbolid on määratletud siin.

Mustad korpusradiaatorid

Kõik soojad asjad kiirgavad soojuskiirgust, mis on elektromagnetiline kiirgus. Enamiku Maa asjade puhul on see kiirgus infrapunases vahemikus, kuid miski, mis on väga kuum (1000 °C või rohkem), kiirgab nähtavat kiirgust, st valgust. 1800. aastate lõpus uurisid paljud teadlased elektromagnetilise kiirguse lainepikkusi, mis pärinevad musta keha kiirgajatest erinevatel temperatuuridel.

Rayleigh-Jeans'i seadus

Lord Rayleigh avaldas Rayleigh-Jeans'i seaduse põhialused esimest korda 1900. aastal. See teooria põhines gaaside kineetilisel teoorial. Sir James Jeans avaldas täielikuma teooria 1905. aastal. Seadus seostab musta keha radiaatorist erinevate temperatuuride juures eralduva elektromagnetilise energia kogust ja lainepikkust. Seda kirjeldav võrrand on:

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}}.

Pika lainepikkusega kiirguse puhul vastasid selle võrrandiga ennustatud tulemused hästi laboris saadud praktilistele tulemustele. Lühikese lainepikkuse (ultraviolettvalgus) puhul oli erinevus teooria ja praktika vahel siiski nii suur, et see teenis hüüdnime "ultraviolettkatastroof".

Plancki seadus

1895. aastal avaldas Wien oma uurimistulemused musta keha kiirguse kohta. Tema valem oli:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda kT}}}} .

See valem töötas hästi lühikese lainepikkusega elektromagnetilise kiirguse puhul, kuid ei töötanud hästi pikkade lainepikkuste puhul.

1900. aastal avaldas Max Planck oma uuringute tulemused. Ta püüdis välja töötada musta keha kiirguse väljenduse lainepikkuses väljendatuna, eeldades, et kiirgus koosneb väikestest kvantidest, ja seejärel näha, mis juhtub, kui kvandid muutuvad lõpmatult väikseks. (See on tavaline matemaatiline lähenemine). Väljend oli järgmine:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}~{\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}}} .

Kui valguse lainepikkusel lastakse muutuda väga suureks, siis võib näidata, et Raleigh-Jeans'i ja Plancki seosed on peaaegu identsed.

Ta arvutas h ja k ning leidis, et

h = 6,55×10⁻²⁷erg-sek.

k = 1,34×10⁻¹⁶erg-deg ^-1.

Need väärtused on lähedased tänapäeval tunnustatud väärtustele, mis on ⁻¹⁶vastavalt 6,62606×10⁻³⁴ ja 1,38065×10. Plancki seadus sobib hästi kokku eksperimentaalsete andmetega, kuid selle täielikku tähtsust hakati hindama alles mitu aastat hiljem.

Valguse kvantteooria

Selgub, et elektronid eemalduvad fotoelektrilise efekti tõttu, kui valgus saavutab lävissageduse. Sellest madalamal ei saa metallist elektronid eralduda. 1905. aastal avaldas Albert Einstein selle efekti selgitava artikli. Einstein pakkus välja, et valgusvihk ei ole mitte ruumis leviv laine, vaid pigem diskreetsete lainepakettide (footonite) kogum, millest igaühel on energia. Einstein ütles, et efekt tuleneb elektroni tabanud footonist. See näitas valguse osakeste olemust.

Einstein leidis ka, et pika lainepikkusega elektromagnetiline kiirgus ei avalda mingit mõju. Einstein ütles, et see oli tingitud sellest, et "osakesed" ei omanud piisavalt energiat, et elektronid häirida.

Plank pakkus välja, et iga fotoni energia on seotud fotoni sagedusega Plancki konstandi abil. Seda võib matemaatiliselt kirjutada järgmiselt:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }} .

Plank sai 1918. aastal Nobeli preemia, millega tunnustati tema teeneid füüsika edendamisel energiakvantide avastamisega. 1921. aastal sai Einstein Nobeli preemia Plancki konstandi sidumise eest fotoelektrilise efektiga.

Illustratsioon on võetud Newtoni originaalkirjast Kuninglikule Seltsile (1. jaanuar 1671 [Juliuse kalender]). S tähistab päikesevalgust. Valgus tasandite BC ja DE vahel on värviline. Need värvid kombineeruvad uuesti, et moodustada päikesevalgus tasapinnal GH


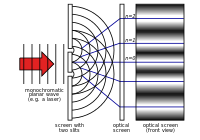
Youngi kahekordse pilu katse


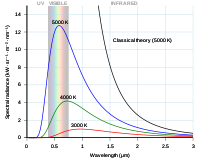
Rayleigh-Jeans'i kõver ja Plancki kõver, mis on esitatud fotoni lainepikkuse suhtes.


Solway konverents 1911. Planck, Einstein ja Jeans seisavad. Planck on vasakult teine. Einstein on teine paremalt. Jeans on paremalt viies. Wien istub, kolmas paremalt.

Rakendus

Plancki konstant on oluline paljudes rakendustes. Mõned neist on loetletud allpool.

Bohri aatomi mudel

1913. aastal avaldas Niels Bohr Bohri aatomi struktuuri Bohri mudeli. Bohr väitis, et elektronide nurkkiirusel, mis liigub ümber tuuma, võivad olla ainult teatud väärtused. Need väärtused on antud võrrandiga

L = n h 2 π {\displaystyle L=n{\frac {h}{2\pi }}}

kus

L = tasandiga seotud nurkmoment.

n = positiivne täisarv.

h = Plancki konstant.

Bohri aatomi mudelit saab kasutada elektronide energia arvutamiseks igal tasemel. Elektronid täidavad tavaliselt aatomi madalaima numbriga olekuid. Kui aatom saab energiat näiteks elektrivoolust, ergastuvad elektronid kõrgemasse olekusse. Seejärel langevad elektronid tagasi madalamasse olekusse ja kaotavad oma täiendava energia fotoni eraldamise teel. Kuna energiatasemetel on kindlad väärtused, siis on ka fotoonidel kindlad energiatasemed. Selliselt kiiratud valgust saab prisma abil jagada erinevateks värvideks. Igal elemendil on oma muster. Neooni muster on näidatud kõrval.

Heisenbergi määramatuse põhimõte

1927. aastal avaldas Werner Heisenberg määramatuse printsiibi. See põhimõte väidab, et mõõtmist ei ole võimalik teha ilma mõõdetavat asja häirimata. Samuti seab see piiriks minimaalse häirituse, mida mõõtmine põhjustab.

Makroskoopilises maailmas teevad need häired väga vähe vahet. Näiteks kui mõõdetakse vedelikku sisaldava kolvi temperatuuri, neelab termomeeter kuumenedes väikese koguse energiat. See põhjustab väikese vea lõppnäituses, kuid see viga on väike ja ei ole oluline.

Kvantmehaanikas on asjad teisiti. Mõned mõõtmised tehakse hajutatud footonite mustrit vaadates. Üks selline näide on Comptoni hajumine. Kui mõõdetakse nii osakese asukohta kui ka impulssi, siis määramatuse põhimõte ütleb, et impulsi mõõtmise täpsuse ja asendi mõõtmise täpsuse vahel on kompromiss. Seda kompromissi kirjeldav võrrand on järgmine:

Δ x Δ p ≳ h {\displaystyle \Delta x\,\Delta p\gtrsim h\qquad \qquad \qquad \qquad }

kus

Δp = impulsi määramatus.

Δx = asukoha määramatus.

h = Plancki konstant.

Valgusdioodide värvus

Paremal kujutatud elektriskeemis sõltub pingelangus valgusdioodi (LED) kohal LED-i materjalist. Ränidioodide puhul on langus 0,6 V. LEDide puhul on see aga vahemikus 1,8-2,7 V. See teave võimaldab kasutajal arvutada Plancki konstanti.

Energia, mis on vajalik ühe elektroni jaoks potentsiaalibarjääri ületamiseks LED-materjalis, on antud järgmiselt

E = Q e V L {\displaystyle E=Q_{e}V_{L}\,}

kus

Q_e on ühe elektroni laeng.

V_L on pinge langus LEDi kohal.

Kui elektron laguneb tagasi, kiirgab ta ühe valgusfotoni. Fotoni energia on antud sama võrrandiga, mida kasutatakse fotoelektrilise efekti puhul. Kui need võrrandid kombineerida, siis on valguse lainepikkus ja pinge seotud järgmise valemiga

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}}}\,}

Selle suhte põhjal saab arvutada alljärgneva tabeli.

Värv	Lainepikkus (nm)	Pinge
punane tuli	650	1.89
roheline tuli	550	2.25
sinine valgus	470	2.62

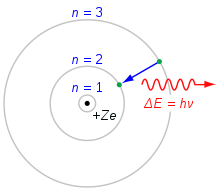
Bohri aatomi mudel. Elektron, mis langeb n=3 kestalt n=2 kestale, kaotab energiat. See energia kandub ära ühe fotoonina.


Neooni nähtav spekter. Iga joon tähistab erinevat energiatasemepaari.


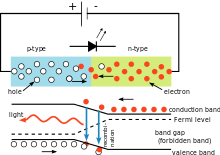
Lihtne LED-ahel, mis illustreerib Plancki konstandi kasutamist. Välja kiiratava valguse värvus sõltub dioodi kohal olevast pingelangusest. Valguse lainepikkust saab arvutada Plancki konstandi abil.

Plancki konstandi väärtus ja kilogrammi ümbermääratlus

Pärast selle avastamist on h mõõtmine muutunud palju paremaks. Planck andis esimesena h väärtuseks 6,55×10 ⁻²⁷erg-sek. See väärtus on 5% piires praegusest väärtusest.

3. märtsi 2014. aasta seisuga on h parimad mõõtmistulemused SI-ühikutes 6,62606957×10 ⁻³⁴J-s. Vastav näitaja cgs ühikutes on 6,62606957×10 ⁻²⁷erg-sek. H suhteline mõõtemääramatus on 4,4×10 . ⁻⁸

Vähendatud Plancki konstant (ħ) on väärtus, mida mõnikord kasutatakse kvantmehaanikas. See on defineeritud järgmiselt

ℏ = h 2 π {\displaystyle \hbar =\frac {h}{2\pi }}.

Kvantmehaanikas kasutatakse mõnikord SI-ühikute asemel Plancki ühikuid. Selles süsteemis on redutseeritud Plancki konstandi väärtus 1, seega on Plancki konstandi väärtus 2π.

Plancksi konstanti saab nüüd väga suure täpsusega mõõta. See on pannud BIPMi kaaluma kilogrammi uut määratlust. Rahvusvahelist kilogrammi prototüüpi ei kasutata enam kilogrammi määratlemiseks. Selle asemel määratleb BIPM Plancki konstandi täpse väärtuse. Teadlased kasutavad seda väärtust ning meetri ja sekundi määratlusi kilogrammi määratlemiseks.

 

Plancki teoreetilise konstandi väärtus

Plancki konstanti saab ka matemaatiliselt tuletada:

 

h = μ 0 π 12 c 3 [ q 0 [ 0,9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6.63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}}{[{q_{0}}}{[0.9163a_{0}]}^{2}]^{2}}}{f_{1r}}^{5}\cdot {s}=6.63\times 10^{-34}J\cdot s}

Siin μ 0 {\displaystyle \mu _{0}} on vaba ruumi läbilaskvus, c {\displaystyle c} on valguse kiirus, q 0 {\displaystyle q_{0}} on elektroni elektrilaeng, a 0 {\displaystyle a_{0}} on Bohri raadius ja f 1 r {\displaystyle f_{1r}} on elektroni pöörlemissagedus vesinikuaatomis ( f 1 r = 3.29 × 10 15 r e v / s ) {\displaystyle (f_{1r}=3.29\t korda 10^{15}rev/s)} . Kui need konstandi väärtused asendada teoreetilise Plancki konstandiga, on teoreetilise Plancki konstandi väärtus täpselt võrdne eksperimentaalse väärtusega.

Seotud leheküljed

• Laine-osakese duaalsus