Heisenbergi määramatuse põhimõte

Segadus vaatleja efektiga

Ajalooliselt on mõõtemääramatuse printsiipi segi aetud füüsikas mõnevõrra sarnase efektiga, mida nimetatakse vaatleja efektiks. See ütleb, et mõnede süsteemide mõõtmisi ei saa teha ilma neid süsteeme mõjutamata. Heisenberg pakkus sellist vaatleja efekti kvantide tasandil kvantmääramatuse füüsikalise "seletusena".

Nüüdseks on aga selge, et määramatuse põhimõte on kõigi lainelaadsete süsteemide omadus. See tuleneb kvantmehaanikas lihtsalt kõigi kvantobjektide aine lainepõhisusest. Seega väljendab määramatuse põhimõte tegelikult kvandsüsteemide fundamentaalset omadust ja ei ole väide praeguse tehnoloogia vaatlusvõime kohta. "Mõõtmine" ei tähenda ainult protsessi, milles osaleb füüsik-vaatleja, vaid pigem igasugust vastastikmõju klassikaliste ja kvantobjektide vahel, sõltumata mis tahes vaatlejast.

Määramatuse idee

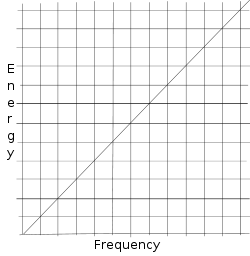
Määramatuse põhimõte pärineb Werner Heisenbergi maatriksmehaanikast. Juba Max Planck teadis, et valguse ühiku energia on proportsionaalne selle valguse ühiku sagedusega ( E ∝ ν {\displaystyle E\propto \nu } ) ja et selle energiahulka saab väljendada tuttavates terminites, nagu džauli, kasutades proportsionaalsuse konstanti. Tema poolt antud konstanti nimetatakse nüüd Plancki konstandiks ja seda tähistatakse tähega h. Kui kvantmehaanika väljendamiseks kasutatakse maatriksit, tuleb sageli kaks maatriksit korrutada, et saada kolmas maatriks, mis annab vastuse, mida füüsik püüab leida. Kuid korrutades sellist maatriksit nagu P (impulsi jaoks) sellise maatriksiga nagu X (asendi jaoks), saadakse teistsugune vastusmaatriks kui siis, kui korrutatakse X P-ga. P ja X korrutamisel X-ga ja seejärel nende võrdlemisel saadakse alati tegurina Plancki konstant. Plancki konstandi kirjutamiseks kasutatav arv sõltub alati kasutatavast mõõtmissüsteemist. (Teatud mõõtmissüsteemi puhul on selle arvväärtus üks.) Paremal asuva diagrammi joone kalle, mis näitab sageduse ja energia suhet, sõltub samuti valitud mõõtmissüsteemist.

Järgmised diagrammid näitavad, mis juhtub, kui me püüame mõõta nii asukohta kui ka impulssi.

Selle matemaatilise avastuse praktiline tulemus on see, et kui füüsik teeb positsiooni selgemaks, siis muutub impulss vähem selgemaks, ja kui füüsik teeb impulsi selgemaks, siis muutub positsioon vähem selgemaks. Heisenberg ütles, et asjad on "määramata", ja teistele meeldis öelda, et nad on "ebakindlad". Kuid matemaatika näitab, et just maailma asjad on määramata või "hägusad", mitte et inimesed on lihtsalt ebakindlad.

Kitsas auk, hajus fookus


Keskmise vahe vedrudega ülesriputamine võimaldab mõõta impulssi, kuid see liigutab vahe ettearvamatult, nii et teave fotoni asukoha kohta keskel läheb kaduma.


Vedrule paigaldatud ava mõõdab hoogu


Vahe kitsendamine suurendab kindlust, kus fotoon keskel on, kuid siis muutub selle suund sealt paremal asuvale avastamisekraanile vastavalt ebakindlamaks.


Lai ava, terav fookus

Määramatuse matemaatilisse vormi viimine

Siinkohal näitame esimest võrrandit, mis andis hiljem Heisenbergi määramatuse printsiibis esitatud põhiidee.

Heisenbergi 1925. aasta teedrajavas töös ei kasutata ega mainita isegi mitte maatriksit. Heisenbergi suur edu oli "skeem, mis oli põhimõtteliselt võimeline üheselt määrama vesinikukiirguse asjakohased füüsikalised omadused (üleminekusagedused ja amplituudid)".

Pärast seda, kui Heisenberg oli kirjutanud oma läbimurdelise töö, andis ta selle ühele oma õpetajale parandamiseks ja läks puhkusele. Max Born oli hämmastunud võrranditest ja mittekommuteerivatest võrranditest, mida isegi Heisenberg pidas probleemiks. Mitme päeva pärast sai Born aru, et need võrrandid olid juhised maatriksite välja kirjutamiseks. Maatriksid olid isegi tolleaegsetele matemaatikutele uued ja kummalised, aga kuidas nendega matemaatikat teha, oli juba selgelt teada. Ta ja mõned teised töötasid kõik välja maatriksvormi kujul, enne kui Heisenberg oma puhkust tagasi tuli, ja mõne kuu jooksul andis uus kvantmehaanika maatriksvormi kujul neile aluse veel üheks paberiks.

Max Born nägi, et kui pq ja qp maatriksid arvutatakse, ei ole need võrdsed. Heisenberg oli juba näinud sama asja oma algse kirjutusviisi järgi ja Heisenberg võis aimata seda, mis oli Bornile peaaegu kohe ilmselge - et pq ja qp vastusmaatriksite vahe oleks alati seotud kahe teguriga, mis tulid välja Heisenbergi algsest matemaatikast: Plancki konstant h ja i, mis on ruutjuur negatiivsest ühest. Nii et just see, mida Heisenberg eelistas nimetada "määramatuse printsiibiks" (tavaliselt tuntud kui määramatuse printsiip), oli Heisenbergi algsetes võrrandites peidus.

Heisenberg oli uurinud muutusi, mis toimuvad aatomis, kui elektron muudab oma energiataset ja satub seega aatomi keskusele lähemale või keskusest kaugemale, ning eriti olukordi, kus elektron langeb kahe sammuga madalamale energiatasemele. Max Born selgitas, kuidas ta võttis Heisenbergi kummalise "retsepti", et leida aatomi mõne muutuse produkt C, mis tuleneb aatomi energiast n energiatasemelt n-b, mis seisneb selles, et võetakse summa, mis saadakse, kui korrutatakse üks muutus, mida nimetatakse A (mis võib olla näiteks mõne fotoni sagedus), mis tekib aatomi elektroni energia muutumisel energiast n ja energiast n-a), järgneva muutusega, mida nimetatakse B (mis võib olla näiteks muutuse amplituud), mis tekib teise energiast n-a ja n-b vahelisel muutumisel:)

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

ja avastasin midagi murrangulist:

Arvestades ...näiteid...[Heisenberg] leidis selle reegli..... See oli 1925. aasta suvel. Heisenberg...võttis puhkuse...ja andis oma töö mulle avaldamiseks üle.....

Heisenbergi korrutamisreegel ei jätnud mulle rahu, ja pärast nädalast intensiivset mõtlemist ja katsetamist tuli mulle äkki meelde algebraline teooria....Sellised kvadraatilised massiivid on matemaatikutele üsna tuttavad ja neid nimetatakse maatriksiteks, mis on seotud kindla korrutamisreegliga. Rakendasin seda reeglit Heisenbergi kvantitatiivsele tingimusele ja leidsin, et see kattub diagonaalelementide puhul. Oli lihtne arvata, mis peavad ülejäänud elemendid olema, nimelt null; ja kohe seisis minu ees kummaline valem

Q P - P Q = i h 2 π {\displaystyle {QP-PQ={\frac {ih}{2\pi }}}}
[Sümbol Q on nihke maatriks, P on impulsi maatriks, i tähistab negatiivse ühe ruutjuurt ja h on Plancki konstant].

Hiljem pani Heisenberg oma avastuse teise matemaatilisse vormi:

Δ x Δ p ≥ ℏ 2 {\displaystyle \Delta x\,\Delta p\geq {\frac {\hbar }{2}}}

(Erilist sümbolit ℏ nimetatakse h-baariks ehk "redutseeritud Planks'i konstandiks", see on võrdne h 2 π {\displaystyle {\frac {h}{2\pi}) .)

Matemaatika on viis kirjeldada asju, mis toimuvad reaalses maailmas. Võiksite ette kujutada, et oleks lihtne saada korraga nii millegi täpset asukohta kui ka selle täpset massi, teekonda ja kiirust. Tegelikkuses tuleb aga vastuse saamiseks teha kaks asja. Kui te mõõdate kusagil suure mäe kaljusse kinni jäänud kuuli asukohta ja impulssi, on asi lihtne. Mägi ei paista kuhugi liikuvat, nagu ka kuul. Seega on selle asukoht teada ja kiirus on 0, seega on ka selle impulss 0. Kui aga kuul on kuskil relva ja sihtmärgi vahel, siis on raske saada selle asukohta igal ajahetkel. Parim, mida me ehk suudame teha, on pildistada seda väga kiire säriajaga kaameraga. Kuid üheainsa säriaja vajutus annaks ainult ühe asja, nimelt kuuli asukoha ajahetkel t. Impulsi saamiseks võime panna kuuli teele parafiiniploki ja mõõta, kuidas parafiiniplokk liikus, kui see kuuli peatas. Või kui me teame kuuli massi, võime teha kahe pildi seeria, arvutada kiiruse, teades kuuli kahe asendi erinevust ja kahe ilmumise vahelist aega. Kuidas iganes me seda ka ei teeks, peame mõõtma massi ja asukohta ning aega ilmumiste vahel. Lõpuks teeme vähemalt kaks mõõtmist, et saada x ja p. Sellisel juhul peame valima, millise mõõtmise teeme esimesena ja millise teisena. Tundub, et pole vahet, millises järjekorras meie mõõtmised tehakse. Kui mõõdame kuuli massi ja seejärel mõõdame kaks korda selle asendeid või kui mõõdame kaks korda kuuli asendeid ja seejärel võtame kuuli tagasi ja mõõdame selle massi, siis ei oleks ju mingit vahet, või? Lõppude lõpuks ei ole me kuuliga midagi teinud, kui me seda kaalume või kui me seda pildistame.

Väga väikesel skaalal, kui me mõõdame midagi sellist nagu elektron, teeb aga iga mõõtmine sellega midagi. Kui me mõõdame kõigepealt asukohta, siis muudame selle momemtumi. Kui me mõõdame kõigepealt elektroni impulssi, siis muudame selle positsiooni. Meie lootus oleks mõõta ühte neist ja seejärel mõõta teist, enne kui midagi muutub, kuid meie mõõtmine ise muudab midagi, ja parim, mida me saame loodetavasti teha, on vähendada miinimumini energiat, mida me elektroni mõõtmisega kaasa anname. Selle minimaalse energiahulga üheks teguriks on Plancki konstant.

Ebakindlus ületab maatriksmatemaatika

Heisenbergi määramatuse põhimõte leiti "uue" kvantfüüsika esimestes võrrandites ja teooria anti maatriksmatemaatika abil. Kuid määramatuse printsiip on looduse fakt ja see ilmneb ka teistes kvantfüüsikast rääkides, näiteks Erwin Schrödingeri tehtud võrrandites.

Looduse määramatus, mitte inimeste määramatus

Heisenbergi avastust on vaadeldud kahel väga erineval viisil: Mõned inimesed arvavad, et looduses toimuvad asjad on "deterministlikud", st asjad toimuvad kindla reegli järgi ja kui me teaksime kõike, mida peame teadma, siis saaksime alati öelda, mis juhtub järgmisena. Teised inimesed arvavad, et looduses toimuvad asjad juhinduvad ainult tõenäosusest ja me saame teada ainult seda, kuidas asjad keskmiselt käituvad - aga me teame seda väga täpselt.

Füüsik John Stewart Bell avastas viisi, kuidas tõestada, et esimene viis ei saa olla õige. Tema tööd nimetatakse Belli teoreemiks või Belli ebavõrdsuseks.

Rahvakultuur

Väljendit "kvanthüpe" või "kvanthüpe" on kasutatud kui mingit suurt ja ümberkujundavat muutust ning seda kasutatakse sageli poliitikute ja massimeedia müügikampaaniate hüperboolses väljenduses. Kvantmehaanikas kasutatakse seda, et kirjeldada elektroni üleminekut ühelt orbiidilt ümber aatomi tuuma mõnele teisele, kõrgemale või madalamale orbiidile.

Mõnikord kasutatakse sõna "kvant" äritoodete ja ettevõtete nimedes. Näiteks Briggs and Stratton toodab mitmesuguseid väikeseid bensiinimootoreid muruniidukitele, pöörlevatele mullaharijatele ja muudele sellistele väikestele masinatele. Üks nende mudelite nimedest on "Quantum".

Kuna mõõtemääramatuse põhimõte ütleb meile, et teatud mõõtmisi aatomi tasandil ei saa teha ilma teisi mõõtmisi häirimata, kasutavad mõned inimesed seda ideed, et kirjeldada inimmaailmas esinevaid juhtumeid, kus vaatleja tegevus muudab vaadeldavat asja. Antropoloog võib minna mõnda kaugesse paika, et teada saada, kuidas inimesed seal elavad, kuid asjaolu, et võõras inimene välismaailmast jälgib neid, võib muuta nende inimeste käitumist.

Asjad, mida inimesed teevad asju vaadeldes, mis muudavad vaadeldavat, on vaatleja efekti juhtumid. Mõned asjad, mida inimesed teevad, põhjustavad muutusi aatomite väga väikesel tasandil ja on määramatuse või määramatuse juhtumid, mida esimesena kirjeldas Heisenberg. Määramatuse printsiip näitab, et alati on piir, kui väikeseid mõõtmispaare, näiteks asukohta ja kiirust või trajektoori ja impulssi, me saame teha. Vaatleja efekt ütleb, et mõnikord võib see, mida inimesed teevad asju vaadeldes, näiteks uurides sipelgapesakonna kohta, kaevates seda aiatööriistadega, avaldada suurt mõju, mis muudab seda, mida nad püüdsid teada saada.