3D ehk kolmemõõtmeline ruum: mõiste, mõõtmed ja rakendused

3D (või 3-D) tähendab kolmemõõtmelist või kolmemõõtmelist. Näiteks karp on kolmemõõtmeline; see on tahke ja mitte õhuke nagu paber. Sellel on ruumala, ülemine ja alumine osa, vasak ja parem (külg), samuti esi- ja tagumine osa. Karbi saab ümber pöörata, et vaadata seda teiselt poolt (mida nimetatakse näo, pinna või lihtsalt küljeks).

Mõiste ja näited

Kolmemõõtmeline ruum tähendab, et objektil on kolm sõltumatut mõõdet, mida saab mõõta eri suundades. Tavapärased näited 3D-objektidest on kuup, sfäär, silinder ja erinevad igemetest koosnevad esemed nagu mööbel või hooned. 3D-objektil on tavaliselt pinnad (faces), servad (edges) ja tipud (vertices), mis kirjeldavad selle geomeetriat.

Mõõtmed ja koordinaadid

Mõõtmed on mõõdetavad tollides, mikronites, miilides, kilomeetrites või muudes pikkusühikutes. Neid kolme mõõdet nimetatakse sageli pikkuseks (või sügavuseks), laiuseks (või laiuseks) ja kõrguseks. Mõnel otstarbel kasutatakse ka teisi sõnu.

Tavaliselt kirjeldatakse punkti kolmemõõtmelises ruumis koordinaatsüsteemis kolme arvuga (x, y, z), kus iga koordinat näitab punkti asukohta vastavas suunas. See on aluseks arvuti‑modelleerimisele, inseneritööle ja füüsikale.

Pind ja ruumala

Kolmemõõtmelisel objektil on pind (mitme näo kogum) ning sees olev ruum, mida nimetatakse ruumala. Ruumala saab arvutada sõltuvalt objekti kujust:

Risttahuka (karbi) ruumala = pikkus × laius × kõrgus.
Kuubi ruumala = a³, kus a on kuubi külje pikkus.
Sfääri ruumala = 4/3 × π × r³, kus r on raadius.

Ruumala mõõtühik on kuupühik (näiteks kuupmeeter, kuupsentimeeter).

Kuidas inimesed ja seadmed näevad 3D-d

Binokulaarne nägemine ehk kahe silma koostöö aitab inimestel hõlpsasti näha kolmandat mõõdet — sügavust. Silmad näevad sama stseeni veidi erinevast vaatenurgast, mistõttu aju tõlgendab kauguse ja ruumilise paigutuse. Lisatehnoloogiad, mis taastavad või võimendavad sügavustaju, on näiteks stereoskoopia, virtuaalreaalsus (VR) ja mõned 3D-kinod.

Arvutite ja ekraanide puhul luuakse 3D‑mulje perspektiivi, varjude, varjutuse (sh varjutuskaartide ja valgustuse arvutamise) ning varaliste renderdamiste abil. 3D-kujude realistlikuks kuvamiseks on vaja palju arvutusi ning selleks kasutatakse sageli graafikaprotsessoreid: kaasaegsetel arvutitel on tavaliselt graafikaprotsessor (GPU), mis tegeleb nende arvutustega. Lisaks eksisteerivad tehnoloogiad nagu anaglüüüf‑prillid, polariseerivad prillid ja aktiivsed särgiprillid 3D-efekti väljatoomiseks.

Rakendused

3D‑kontseptsioonil on lai kasutusala igapäevaelus, teaduses ja tööstuses. Mõned olulisemad rakendused:

3D-graafikat kasutatakse videomängude ja animafilmide loomiseks — mudelid koos tekstuuride, valgustuse ja animatsiooniga annavad kolmemõõtmelise tulemuse.
3D‑modelleerimine ja CAD (arvutipõhine projekteerimine) on oluline inseneritöös, arhitektuuris ja tootearenduses.
3D‑printimine võimaldab toota füüsilisi esemeid otse digitaalsest mudelist, kasutades mitmesuguseid materjale.
Meditsiinis kasutatakse 3D‑pildistamist (nt CT, MRI) patsientide sise‑struktuuride visualiseerimiseks ja kirurgiliseks planeerimiseks.
Kaardistuses ja geoloogias kasutatakse kolmemõõtmelisi mudeleid maastiku ja maa-aluste struktuuride analüüsiks.
3D‑skaneerimine ja fotogramm-meetria võimaldavad reaalsete objektide täpset digitaliseerimist ja arhiveerimist.

Andmestruktuurid ja arvutus

Arvutigraafikas salvestatakse 3D‑objekte tavaliselt kolmemõõtmelise geomeetria vormis nagu nurkstikud ja kolmnurkvõrgustikud (mesh), tarkvarasse kuuluvad tekstuurid, materjalid ja valgustingimused. Renderdamisel teisendatakse see info 2D‑pildiks kasutaja ekraanil, arvestades kaameranurka, perspektiivi ja valgustamist. Reaalaegsuslike rakenduste (näiteks mängude) puhul on oluline optimeerimine, GPU‑akselereerimine ja varjude/peegelduste ligikaudne arvutus, et saavutada sujuv pildikvaliteet.

Kokkuvõte

3D ehk kolmemõõtmeline ruum kirjeldab maailmas asuvate objektide kuju ja paiknemist kolme sõltumatu mõõtme abil. See mõiste ulatub elementaarsetest geomeetrilistest kujunditest kuni keerukate digimudelite ja reaalse maailma rakendusteni nagu meditsiin, inseneriteadus, meelelahutus ja tootmine. Mõistmine, kuidas mõõta ja esitada 3D‑ruumi, on tänapäeva tehnoloogiamaailmas oluline oskus.

3D-karp

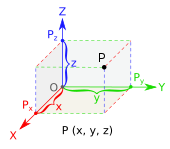
Pilt "X-teljest", "Y-teljest" ja "Z-teljest".

3D matemaatiline joonis või graafik, millel on laiust, kõrgust ja pikkust mõõtvad jooned.

Matemaatikas

Kartesiaanlikus koordinaatsüsteemis on pikkus, laius ja kõrgus esitatud tähtedega (muutujad), et neid oleks lihtsam kirjutada või kui väärtus ei ole teada. Sageli on X laius, Y kõrgus ja Z pikkus. Teised 3D-koordinaatsüsteemid, näiteks sfäärilised koordinaadid, sisaldavad nii lineaarseid kui ka nurgamõõtmisi.

3D-kujude ja -mõõtmete matemaatilist uurimist nimetatakse tahke geomeetriaks.

Aeg

Mõned inimesed näevad aega kui neljandat mõõdet. Ka seda mõõdetakse. Seda mõõdetakse ajaühikutes, nagu sekundid, tunnid, aastad või mõni muu ajaühik.

Seotud leheküljed

Küsimused ja vastused

K: Mida tähendab 3D?

V: 3D tähendab kolmemõõtmelist või kolmemõõtmelist.

K: Kuidas saab kirjeldada kasti?

V: Kast on kolmemõõtmeline, ta on tahke ja tal on ruumala. Samuti on tal ülemine ja alumine osa, vasak ja parem (külg) ning esi- ja tagumine osa.

K: Kuidas nimetatakse neid kolme mõõdet?

V: Kolme mõõdet nimetatakse sageli pikkuseks (ehk sügavuseks), laiuseks (ehk laiuseks) ja kõrguseks.

K: Milleks kasutatakse 3D-graafikat?

V: 3D-graafikat kasutatakse videomängude või animafilmide tegemiseks.

K: Millega on tänapäevased arvutid võimelised 3D-graafikaga toime tulema?

V: Kaasaegsetel arvutitel on tavaliselt graafikaprotsessor (GPU), mis tegeleb nende arvutustega.

K: Mis aitab inimestel hõlpsasti näha kolmandat mõõdet?

V: Binokulaarne nägemine aitab inimestel hõlpsasti näha kolmandat mõõdet.

K: Kuidas muudetakse pildid ekraanil kolmemõõtmeliseks?

V: Selleks, et pilte ekraanil kolmemõõtmelistena kujutada, on vaja teha palju arvutusi.