Punktiproduktsioon

Määratlus

Kahe vektori a = [a₁ , a₂ , ..., a_n ] ja b = [b₁ , b₂ , ..., b_n ] punktprodukt on defineeritud järgmiselt:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}}

kus Σ tähistab summeerimisnootatsiooni ( kõikide terminite summa) ja n on vektorruumi mõõde.

Mõõtmes 2 on vektorite [a,b] ja [c,d] punktproduktsioon ac + bd. Samamoodi on 3. dimensioonis vektorite [a,b,c] ja [d,e,f] punktprodukt ad + be + cf. Näiteks kahe kolmemõõtmelise vektori [1, 3, -5] ja [4, -2, -1] punktprodukt on

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.}

Geomeetriline tõlgendus

Eukleidilises geomeetrias on punktproduktsioon, pikkus ja nurk seotud. Vektori a puhul on punktproduktsioon a - a pikkuse a ruut või

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}}

kus ||a|| tähistab a pikkust (suurust). Üldisemalt, kui b on teine vektor.

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|cos \theta \,}

kus ||a| ja ||b| tähistavad a ja b pikkust ning θ on nende vaheline nurk.

Seda valemit saab ümber korraldada, et määrata kahe nullist erineva vektori vahelise nurga suurus:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {\mathbf {a}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}\right\|\left\|{\mathbf {b}}\right\|}}\right)}

Vektorid võib ka kõigepealt teisendada ühikvektoriteks, jagades nende suuruse järgi:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\||}}}

siis on nurk θ antud järgmiselt

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}\cdot {\boldsymbol {\hat {b}})})

Kuna 90° kosinus on null, siis on kahe ortogonaalse (risti) vektori punktproduktsioon alati null. Lisaks sellele võib kahte vektorit pidada ortogonaalseks, kui nende punktproduktsioon on null ja kui nende mõlema pikkus ei ole null. See omadus annab lihtsa meetodi ortogonaalsuse tingimuse kontrollimiseks.

Mõnikord kasutatakse neid omadusi ka punktprodukti defineerimiseks, eriti 2- ja 3-mõõtmelistes ruumides; see definitsioon on samaväärne ülaltoodud määratlusega. Suuremate mõõtmete puhul võib valemit kasutada nurga mõiste defineerimiseks.

Geomeetrilised omadused sõltuvad sellest, et alus on ortonormaalne, st koosneb paarikaupa risti asetsevatest vektoritest, mille pikkus on ühik.

Skaalaarprojektsioon

Kui nii a kui ka b on ühepikkused (st nad on ühikuvektorid), siis nende punktproduktsioon annab lihtsalt nende vahelise nurga kosinuse.

Kui ainult b on ühikuvektor, siis punktproduktsioon a - b annab |a| cos(θ), st a projektsiooni suurus b suunas, kusjuures miinusmärk on siis, kui suund on vastupidine. Seda nimetatakse a skalaarprojektsiooniks b peale või a skalaarkomponendiks b suunas (vt joonis). Sellel punktprodukti omadusel on mitmeid kasulikke rakendusi (vt näiteks järgmine lõik).

Kui ei a ega b ei ole ühikvektor, siis on näiteks a projektsiooni suurus b suunas a - (b / |b|), kuna b suunas on ühikvektor b / |b|.

Rotatsioon

Orthonormaalse aluse, mille alusel vektor a on esitatud, pööramine saadakse pööramismaatriksiga R. See maatriksi korrutamine on lihtsalt punktproduktsioonide jada kompaktne esitus.

Näiteks olgu

• B₁ = {x, y, z} ja B₂ = {u, v, w} on sama ruumi R³ kaks erinevat ortonormaalset baasi, kusjuures B₂ saadakse lihtsalt B₁ pööramisega,
• a₁ = (a_x , a_y , a_z ) esindavad vektorit a B₁ tähenduses,
• a₂ = (a_u , a_v , a_w ) kujutavad sama vektorit pööratud aluse B₂ tähenduses,
• u₁ , v₁ , w₁ on pööratud baasvektorid u, v, w, mis on esitatud B kujul.₁

Seejärel toimub pööramine B₁ ja B₂ vahel järgmiselt:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}}_{1}\{\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}. }

Pange tähele, et pöörlemismaatriks R koostatakse, kasutades ridadena pööratud baasvektoreid u₁ , v₁ , w₁ ja need vektorid on ühikvektorid. Definitsiooni järgi koosneb Ra₁ punktproduktsioonidest iga R-i kolme rea ja vektori a₁ vahel. Iga selline punktprodukt määrab a-i skalaarkomponendi pööratud baasvektori suunas (vt eelmine lõik).

Kui₁ on ridade, mitte veergude vektor, siis peab R sisaldama pööratud baasvektoreid oma veergudes ja peab pärast korrutama₁ :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. }

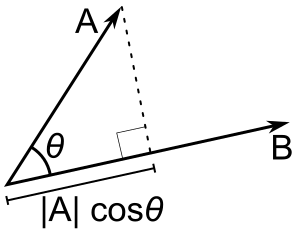
A - B = |A| |B| cos(θ). |A| cos(θ) on A skalaarprojektsioon B-le.

Füüsika

Füüsikas on suurus skalaar füüsikalises mõttes, st koordinaatsüsteemist sõltumatu füüsikaline suurus, mida väljendatakse arvväärtuse ja füüsikalise ühiku korrutisena, mitte lihtsalt arvuna. Punktiproduktsioon on samuti skalaar selles mõttes, mis on antud valemiga, mis ei sõltu koordinaatsüsteemist. Näide:

• Mehaaniline töö on jõu ja nihkevektorite punktproduktsioon.
• Magnetvoog on magnetvälja ja pindala vektorite punktproduktsioon.
• Ruumivooluhulk on vedeliku kiiruse ja pindala vektorite punktproduktsioon.

Omadused

Kui a, b ja c on reaalvektorid ja r on skalaar, kehtivad järgmised omadused.

Punktiproduktsioon on kommutatiivne:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . }

Punktiproduktsioon on distributiivne vektorite liitmisel:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . }

Punktiproduktsioon on bilineaarne:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). }

Kui korrutatakse skalaararvuga, rahuldab punktprodukti:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )} }

(need kaks viimast omadust tulenevad kahest esimesest).

Kaks nullist erinevat vektorit a ja b on risti, kui ja ainult siis, kui a - b = 0.

Erinevalt tavaliste arvude korrutamisest, kus kui ab = ac, siis b on alati võrdne c, kui a ei ole null, ei järgi punktproduktsioon tühistamisseadust:

Kui a - b = a - c ja a ≠ 0, siis saame jaotusseaduse järgi kirjutada: a - (b - c) = 0; ülaltoodud tulemus ütleb, et see tähendab lihtsalt, et a on risti (b - c), mis võimaldab ikkagi (b - c) ≠ 0 ja seega b ≠ c.

Eeldusel, et alus on ortonormaalne, on punktprodukt muutumatu aluse isomeetriliste muutuste korral: pöörete, peegelduste ja kombinatsioonide korral, säilitades alguspunkti fikseerituna. Eespool nimetatud geomeetriline tõlgendus tugineb sellele omadusele. Teisisõnu, ortonormaalse ruumi puhul, millel on mis tahes arv mõõtmeid, on punktproduktsioon muutumatu ortogonaalsel maatriksil põhineva koordinaattransformatsiooni korral. See vastab järgmistele kahele tingimusele:

• Uus alus on jälle ortonormaalne (st see on ortonormaalne, väljendatuna vanas alusena).
• Uued baasvektorid on sama pikad kui vanad (st ühikupikkus vana baasi suhtes).

Kui a ja b on funktsioonid, siis on a - b tuletis a' - b + a - b'.

Kolmikprodukti laiendamine

See on väga kasulik identiteet (tuntud ka kui Lagrange'i valem), mis hõlmab punkt- ja ristprodukti. See kirjutatakse järgmiselt

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )- -\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )} }

mida on lihtsam meeles pidada kui "BAC miinus CAB", pidades silmas, millised vektorid on kokku punktiiritud. Seda valemit kasutatakse tavaliselt vektorarvutuste lihtsustamiseks füüsikas.

Geomeetrilise tõlgenduse tõestus

Vaatleme elementi R ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . . + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,}

Pythagorase teoreemi korduv rakendamine annab selle pikkuse kohta |v|.

| v | 2 = v 1 2 + v 2 2 + . . . . + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,}

Kuid see on sama, mis

v ⋅ v = v 1 2 + v 2 2 + . . . . + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,}

seega järeldame, et vektori v punktprodukti võtmine iseendaga annab vektori pikkuse ruutu.

Lemma 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,}

Vaatleme nüüd kahte vektorit a ja b, mis ulatuvad alguspunktist ja mida lahutab nurk θ. Kolmandat vektorit c võib defineerida järgmiselt

c = d e f a - b . {\displaystyle \mathbf {c} \ \stackrel {\mathrm {def} {=}}\ \mathbf {a} -\mathbf {b} .\,} \,}

moodustades kolmnurga külgedega a, b ja c. Vastavalt kosinuste seadusele on meil

| c | 2 = | a | 2 + | b | 2 - 2 | a | | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} |||\mathbf {b} |\cos \theta .\,}

Asendades punktiproduktiid ruutpikkustele vastavalt Lemma 1, saame järgmise tulemuse

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} (1)

Aga kuna c ≡ a - b, siis on meil ka

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} ,

mis vastavalt jaotusseadusele laieneb kuni

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} (2)

Ühendades kaks c - c võrrandit, (1) ja (2), saame järgmise tulemuse

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Kui mõlemast küljest lahutada a - a + b - b ja jagada -2-ga, jääb tulemuseks

a ⋅ b = | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} |||\mathbf {b} |\cos \theta .\,}

Q.E.D.

Üldistus

Sisemine korrutis üldistab punktprodukti abstraktsetele vektorruumidele ja seda tähistatakse tavaliselt järgmiselt: ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle } . Punktiprodukti geomeetrilise tõlgenduse tõttu on vektori a norm ||a|| sellises sisemise korrutise ruumis defineeritud kui

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}}

nii, et see üldistab pikkust ja kahe vektori a ja b vahelist nurka θ, milleks on

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ ‖ b ‖ . {\displaystyle \cos \theta = \frac \mathbf \a} \,,\mathbf {b} \|\mathbf {a} \|\,\|\|\mathbf {b} \|}}. }

Eelkõige loetakse kaks vektorit ortogonaalseks, kui nende sisemine korrutis on null.

⟨ a , b ⟩ = 0. {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle =0.}

Komplekssete kirjetega vektorite puhul tooks antud punktprodukti määratluse kasutamine kaasa hoopis teistsugused geomeetrilised omadused. Näiteks võib vektori punktproduktsioon iseendaga olla suvaline kompleksarv ja võib olla null, ilma et vektor oleks nullvektor; sellel omakorda oleks tõsised tagajärjed sellistele mõistetele nagu pikkus ja nurk. Paljusid geomeetrilisi omadusi saab päästa skalaarprodukti sümmeetrilistest ja bilineaarsetest omadustest loobumise hinnaga, kui alternatiivselt defineerida järgmine mõiste.

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}}

kus b_i on b _ikomplekskonjugaat. Siis on mis tahes vektori skalaartoot iseendaga mittenegatiivne reaalarv ja see on mittenull, välja arvatud nullvektor. See skalaarproduktsioon ei ole aga lineaarne b-ga (vaid pigem konjugatsiooniline lineaarne) ja skalaarproduktsioon ei ole ka sümmeetriline, sest

a ⋅ b = b ⋅ a ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}} .

Selline skalaarproduktsioon on siiski üsna kasulik ja viib Hermitiuse vormi ja üldiste sisemiste korrutisruumide mõisteteni.

Frobeniuse sisemine korrutis üldistab punktprodukti maatriksitele. See on defineeritud kui kahe sama suurusega maatriksi vastavate komponentide produktide summa.

Üldistamine tensoritele

Korra n tensori ja korra m tensori punktproduktsioon on korra n+m-2 tensor. Punktiprodukti saamiseks korrutatakse ja summeeritakse mõlema tensori üks indeks. Kui A {\displaystyle \mathbf {A} } ja B {\displaystyle \mathbf {B} } on kaks tensorit, mille elementide esitus A i j ... k ℓ ... {\displaystyle A_{ij\dots }^{k\ell \dots }} ja B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}}} on punktprodukti A ⋅ B {\displaystyle \mathbf {A} \cdot \mathbf {B} } on antud järgmiselt

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}}

See määratlus taandub loomulikult standardse vektorite punktprodukti, kui seda rakendatakse vektorite suhtes, ja maatriksite korrutamiseks, kui seda rakendatakse maatriksite suhtes.

Mõnikord kasutatakse kahekordset punktprodukti kahe indeksi korrutamiseks ja summeerimiseks. Kahe 2. järgu tensori topeltpunktiproduktsioon on skalaar.

Seotud leheküljed

• Cauchy-Schwarzi ebavõrdsus
• Risttoode
• Maatriksi korrutamine
• Füüsika