Harmooniline jada (matemaatika)

Matemaatikas on harmooniline jada lahknev lõpmatu jada:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }

Divergentsus tähendab, et kui lisate rohkem termineid, siis summa ei lakka kunagi suurenemast. See ei liigu ühe lõpliku väärtuse suunas.

Lõpmatu tähendab, et alati saab lisada veel ühe termini. Sarjal ei ole lõplikku terminit.

Selle nimi tuleneb muusikas kasutatavast harmooniate ideest: vibreeriva keelpidi ülemtoonide lainepikkused on 1/2, 1/3, 1/4 jne. keelpidi põhilainepikkusest. Peale esimese termini on iga rea termin harmooniline keskväärtus mõlemal pool sellest. Väljend harmooniline keskmine pärineb samuti muusikast.

Ajalugu

Asjaolu, et harmooniline jada lahkneb, tõestas esmakordselt 14. sajandil Nicole Oresme, kuid see unustati. Tõendid andsid 17. sajandil Pietro Mengoli, Johann Bernoulli ja Jacob Bernoulli.

Arhitektid on kasutanud harmoonilisi jadasid. Barokiajastul kasutasid arhitektid neid põhiplaanide ja kõrguste proportsioonides ning kirikute ja paleede arhitektuursete detailide vahelistes suhetes.

Divergence

Harmooniliste seeriate lahknemise kohta on mitu tuntud tõestust. Mõned neist on esitatud allpool.

Võrdlustest

Üks viis diverentsuse tõestamiseks on võrrelda harmoonilist jada teise divergentse jadaga, kus iga nimetaja on asendatud järgmise suurima kahest tuleneva potensiga:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}}+{\frac {1}{8}}}+{\frac {1}{9}}+\cdots \\\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {punane}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{8}}}+{\frac {1}{\color {red}{\mathbf {16}} }}}+\cdots \end{aligned}}}} {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}}

Iga harmoonilise seeria termin on suurem või võrdne teise seeria vastava terminiga, mistõttu harmoonilise seeria summa peab olema suurem või võrdne teise seeria summaga. Teise rea summa on aga lõpmatu:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}}\!+\!{\frac {1}{4}}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}}\!+\!{\frac {1}{8}}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}}} {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}}

Sellest järeldub (võrdlustest), et ka harmooniliste jadade summa peab olema lõpmatu. Täpsemalt, ülaltoodud võrdlus tõestab, et

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}}} {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}}

iga positiivse täisarvu k korral.

Seda Nicole Oresme'i poolt umbes 1350. aastal esitatud tõestust peetakse keskaegse matemaatika kõrgpunktiks. See on tänapäevalgi matemaatikaõpetuses õpetatav standardtõend.

Integraalne test

On võimalik tõestada, et harmooniline jada lahkneb, võrreldes selle summat ebakorrektse integraaliga. Vaadeldakse paremal oleval joonisel kujutatud ristkülikute paigutust. Iga ristküliku laius on 1 ühik ja kõrgus 1/n ühikut, nii et lõpmatu arvu ristkülikute kogupindala on harmoonilise rea summa:

ristkülikute pindala = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{area of}\\\{\text{rectangles}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } {\displaystyle {\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }

Kogu pindala kõvera y = 1/x all alates 1-st kuni lõpmatuseni on antud lahkneva ebakorrektse integraaliga:

kõveraalune pindala = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{rea under}}\\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty . } {\displaystyle {\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .}

Kuna see pindala sisaldub täielikult ristkülikute sees, peab ka ristkülikute kogupindala olema lõpmatu. See tõestab, et

∑ n = 1 k 1 n > ∫ 1 k + 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1). } {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).}

Selle argumendi üldistus on tuntud kui integraalne test.

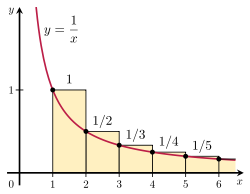
Integraalkatse illustratsioon.Zoom
Integraalkatse illustratsioon.

Erinevuse määr

Harmooniline rida erineb väga aeglaselt. Näiteks esimese 1043 termini summa on väiksem kui 100. See on tingitud sellest, et seeria osisummad on logaritmilise kasvuga. Eelkõige,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1} {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1}

kus γ on Euler-Mascheroni konstant ja εk ~ 1/2k, mis läheneb 0-le, kui k läheb lõpmatusse. Leonhard Euler tõestas nii seda kui ka seda, et summa, mis sisaldab ainult algarvude vasteid, samuti lahkneb, s.t:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty . } {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .}

Osalised summad

Kolmkümmend esimest harmoonilist arvu

n

Harmooniliste jadade osaline summa, Hn

 

väljendatuna murdosana

detsimaalne

suhteline suurus

 

1

1

~1

1

 

 

2

3

/2

~1.5

1.5

 

 

3

11

/6

~1.83333

1.83333

 

 

4

25

/12

~2.08333

2.08333

 

 

5

137

/60

~2.28333

2.28333

 

 

6

49

/20

~2.45

2.45

 

 

7

363

/140

~2.59286

2.59286

 

 

8

761

/280

~2.71786

2.71786

 

 

9

7129

/2520

~2.82897

2.82897

 

 

10

7381

/2520

~2.92897

2.92897

 

 

11

83711

/27720

~3.01988

3.01988

 

 

12

86021

/27720

~3.10321

3.10321

 

 

13

1145993

/360360

~3.18013

3.18013

 

 

14

1171733

/360360

~3.25156

3.25156

 

 

15

1195757

/360360

~3.31823

3.31823

 

 

16

2436559

/720720

~3.38073

3.38073

 

 

17

42142223

/12252240

~3.43955

3.43955

 

 

18

14274301

/4084080

~3.49511

3.49511

 

 

19

275295799

/77597520

~3.54774

3.54774

 

 

20

55835135

/15519504

~3.59774

3.59774

 

 

21

18858053

/5173168

~3.64536

3.64536

 

 

22

19093197

/5173168

~3.69081

3.69081

 

 

23

444316699

/118982864

~3.73429

3.73429

 

 

24

1347822955

/356948592

~3.77596

3.77596

 

 

25

34052522467

/8923714800

~3.81596

3.81596

 

 

26

34395742267

/8923714800

~3.85442

3.85442

 

 

27

312536252003

/80313433200

~3.89146

3.89146

 

 

28

315404588903

/80313433200

~3.92717

3.92717

 

 

29

9227046511387

/2329089562800

~3.96165

3.96165

 

 

30

9304682830147

/2329089562800

~3.99499

3.99499

 

 

Lõplikud osalised summad lahknevate harmooniliste seeriate kohta,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},} {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},}

nimetatakse harmoonilisteks arvudeks.

Hn ja ln n vahe konvergeerub Euler-Mascheroni konstandiga. Kahe mis tahes harmoonilise arvu vahe ei ole kunagi täisarv. Ükski harmooniline arv ei ole täisarv, välja arvatud H1 = 1.

Seotud seeriad

Vahelduv harmooniline jada

Seeria

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots } {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots }

on tuntud kui vahelduv harmooniline jada. See rida konvergeerub vahelduvate seeriate katse abil. Eelkõige on summa võrdne 2 naturaallogaritmiga:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.} {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.}

Vahelduv harmooniline rida on küll tingimuslikult konvergentne, kuid mitte absoluutselt konvergentne: kui seeriatermineid süstemaatiliselt ümber paigutada, muutub summa üldjuhul teistsuguseks ja sõltuvalt ümberpaigutamisest võib see olla isegi lõpmatu.

Vahelduv harmooniline seeria valem on Mercatori seeria erijuht, Taylori seeria naturaalse logaritmi jaoks.

Seotud rea saab tuletada Taylori arktangendi reast:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}. } {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.}

Seda nimetatakse Leibnizi jadaks.

Üldine harmooniline rida

Üldine harmooniline jada on kujul

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},} {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},}

kus a ≠ 0 ja b on reaalarvud ja b/a ei ole null või negatiivne täisarv.

Harmooniliste seeriate piirvõrdlustesti järgi erinevad ka kõik üldised harmoonilised seeriad.

p-seeria

Harmoonilise seeria üldistus on p-seeria (või hüperharmooniline seeria), mis on defineeritud kui

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}} {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}}

mis tahes reaalarvu p korral. Kui p = 1, on p-seeria harmooniline seeria, mis lahkneb. Kas integraaltest või Cauchy kondensatsioonitest näitab, et p-seeria konvergeerub kõigi p > 1 korral (sellisel juhul nimetatakse seda üleharmooniliseks seeriaks) ja divergentseks kõigi p ≤ 1 korral. Kui p > 1, siis on p-seeria summa ζ(p), st Riemanni zeta-funktsioon, mida hinnatakse punktis p.

Summa leidmise probleemi p = 2 korral nimetatakse Baseli probleemiks; Leonhard Euler näitas, et see on π2/6. Summa väärtust p = 3 korral nimetatakse Apéry konstantsiks, sest Roger Apéry tõestas, et see on irratsionaalne arv.

ln-seeria

Seotud p-seeriaga on ln-seeria, mis on määratletud kui

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}} {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}}

mis tahes positiivse reaalarvu p korral. Integraaltestiga saab näidata, et see lahkneb, kui p ≤ 1, kuid konvergeerub, kui p > 1.

φ-seeria

Mis tahes kumerate reaalväärtusega funktsioonide φ puhul, mis on sellised, et

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}}\right)}{\varphi (u)}}<{\frac {1}{2}}},} {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},}

seeria

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)} {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)}

on konvergentne. []

Juhuslik harmooniline rida

Juhuslik harmooniline rida

∑ n = 1 ∞ s n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},} {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},}

kus sn on sõltumatud, identselt jaotunud juhuslikud muutujad, mis võtavad väärtused +1 ja -1 võrdse tõenäosusega 1/2, on tõenäosusteoorias tuntud näide juhuslike muutujate jada kohta, mis konvergeerub tõenäosusega 1. Selle konvergentsi fakt on lihtne tagajärg kas Kolmogorovi kolme seeria teoreemile või sellega tihedalt seotud Kolmogorovi maksimaalsele ebavõrdsusele. Byron Schmuland Alberta Ülikoolist uuris täiendavalt juhusliku harmoonilise seeria omadusi ja näitas, et konvergentsed seeriad on juhuslikud muutujad, millel on mõned huvitavad omadused. Eelkõige võtab selle juhusliku muutuja tõenäosustiheduse funktsioon, mida hinnatakse +2 või -2 juures, väärtuse 0,124999999999999999999999999999999999999999999999999999999999999999999999764..., mis erineb 1/8-st vähem kui 10-42 võrra. Schmulandi artikkel selgitab, miks see tõenäosus on nii lähedal, kuid mitte täpselt 1/8-le. Selle tõenäosuse täpne väärtus on antud lõpmatu kosinusprodukti integraali C2 jagatuna π-ga.

Ammendunud harmooniline rida

On võimalik näidata, et ammendatud harmooniline rida, kus kõik terminid, mille nimetajas esineb number 9, on konvergeerunud ja selle väärtus on väiksem kui 80. Tegelikult, kui eemaldada kõik terminid, mis sisaldavad mingit konkreetset numbrite jada (mis tahes baasil), siis seeria konvergeerub.

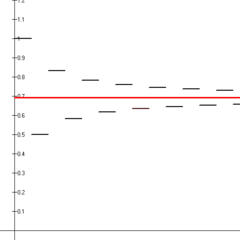
Vahelduvate harmooniliste jadade esimesed neljateistkümme osalist summat (mustad joonsegmendid), mis lähenevad 2 loomulikule logaritmile (punane joon).Zoom
Vahelduvate harmooniliste jadade esimesed neljateistkümme osalist summat (mustad joonsegmendid), mis lähenevad 2 loomulikule logaritmile (punane joon).

Rakendused

Harmooniline rida võib olla vastukaaluks. Seda seetõttu, et tegemist on divergentsete seeriaga, kuigi seeriaterminid muutuvad väiksemaks ja lähevad nulli suunas. Harmoonilise rea divergentsus on mõnede paradokside allikas.

  • "uss kummipaelal". Oletame, et uss roomab mööda lõpmatult elastset ühemeetrist kummilinti, samal ajal kui kummilinti ühtlaselt venitatakse. Kui uss liigub 1 sentimeetri minutis ja lind venib 1 meetri minutis, siis kas uss jõuab kunagi kummilindi lõppu? Vastus on vastupidiselt "jah", sest n minuti pärast on usside läbitud teekonna ja kummilindi kogupikkuse suhe järgmine

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}}. } {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.}

Kuna jada muutub suvaliselt suureks, kui n muutub suuremaks, peab see suhe lõpuks ületama 1, mis tähendab, et uss jõuab kummipaelale. Kuid n väärtus, mille juures see juhtub, peab olema äärmiselt suur: umbes e100, mis on arv, mis ületab 1043 minutit (1037 aastat). Kuigi harmooniline jada lahkneb, teeb ta seda väga aeglaselt.

  • Jeepi probleemi puhul küsitakse, kui palju kütust on vaja kokku, et piiratud kütusekandevõimega auto läbiks kõrbe, jättes marsruudil kütusepisaraid. Teatud kütusekogusega läbitav vahemaa on seotud logaritmiliselt kasvavate harmooniliste jadade osisummadega. Ja nii kasvab nõutav kütus eksponentsiaalselt koos soovitud vahemaaga.
  • Klotside virnastamise probleem: kui on antud kogum ühesuguseid doominosid, siis on võimalik neid laua servale virnastada nii, et nad ripuvad üle laua serva, ilma et nad maha kukuksid. Vastupidine tulemus on see, et neid saab virnastada nii, et üleulatuvus on nii suur kui soovite. Seda tingimusel, et doominoid on piisavalt palju.
  • Ujuja, kes läheb kiiremini iga kord, kui ta puudutab basseini seina. Ujuja alustab 10 meetri pikkuse basseini läbimist kiirusega 2 m/s ja iga läbimisega lisandub kiirusele veel 2 m/s. Teoreetiliselt on ujuja kiirus piiramatu, kuid selle kiiruse saavutamiseks on vaja läbida bassein väga palju kordi; näiteks valguse kiiruse saavutamiseks (kui jätta kõrvale eriline relatiivsusteooria) peab ujuja läbima basseini 150 miljonit korda. Vastupidiselt sellele suurele arvule sõltub antud kiiruse saavutamiseks vajalik aeg mis tahes arvu basseiniületuste seeria summast:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}}. } {\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.}

Summa arvutamine näitab, et valguse kiiruse saavutamiseks kuluv aeg on vaid 97 sekundit.

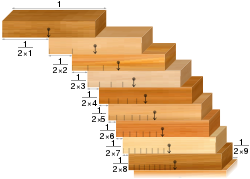
Klotside virnastamise probleem: harmoonilise rea järgi joondatud klotsid ületavad suvalise laiusega lõhed.Zoom
Klotside virnastamise probleem: harmoonilise rea järgi joondatud klotsid ületavad suvalise laiusega lõhed.

Seotud leheküljed

  • Harmooniline areng
  • Vastastikuste summade loetelu

Küsimused ja vastused

K: Mis on harmooniline sari?


V: Harmooniline jada on lõpmatu divergentne jada, mille iga liige on võrdne 1, mis jagatakse tema positsiooniga jadas.

K: Mida tähendab, et jada on divergentne?


V: Divergentne tähendab, et kui lisate rohkem termineid, siis summa ei lakka kunagi suurenemast ega liigu ühe lõpliku väärtuse suunas.

K: Mida tähendab, et jada on lõpmatu?


V: Lõpmatu tähendab, et alati saab lisada veel ühe termini ja sarjale ei ole lõputerminit.

K: Kust pärineb selle rea nimi?


V: Selle rea nimi pärineb muusikas kasutatavast harmooniate ideest, kus ülemtoonide lainepikkused on 1/2, 1/3, 1/4 jne. stringi põhilainepikkusest.

K: Mida tähendab harmooniline?


V: Harmooniline keskmine on see, kui iga termin jadas on võrdne oma naaberterminite harmoonilise keskmisega. See väljend pärineb samuti muusikast.

K: Kuidas me arvutame selle jada iga termi?


V: Iga termi selles jadas saab arvutada, jagades ühe tema positsiooniga jadas (1/n).

AlegsaOnline.com - 2020 / 2023 - License CC3