Logaritmiline skaala
Logaritmiline skaala on skaala, mida kasutatakse siis, kui suur hulk suurusi on suur. Levinumad kasutusalad on näiteks maavärina tugevus, heli helitugevus, valguse intensiivsus ja lahuste pH.
See põhineb pigem suurusjärkudel kui standardsel lineaarsel skaalal. Skaala iga märgi väärtus on eelmise märgi väärtus korrutatud konstantsiga.
Logaritmilisi skaalasid kasutatakse ka arvude korrutamiseks või jagamiseks, lisades või lahutades skaalal olevaid pikkusi.
Logaritmiline skaala võib olla kasulik, kui andmed hõlmavad suurt väärtuste vahemikku - logaritm vähendab seda käepärasemaks.
Mõned meie meeled toimivad logaritmiliselt (tegeliku sisendtugevuse korrutamine lisab tajutud signaalitugevusele konstandi, vt: Stevensi võimsusseadus). See muudab logaritmilised skaalad nende sisendkoguste jaoks eriti sobivaks. Eelkõige tajub meie kuulmismeel sageduste võrdseid korrutisi kui võrdseid helikõrguse erinevusi.
Enamikul logaritmilistel skaaladel vastavad aluseks oleva suuruse väikesed kordajad (või suhtarvud) logaritmimõõdu väikestele (võimalik, et negatiivsetele) väärtustele.
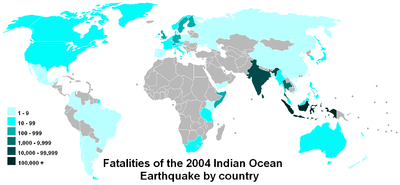
Logaritmiline skaala võimaldab hõlpsasti võrrelda väärtusi, mis hõlmavad suurt vahemikku, nagu näiteks sellel kaardil.
Kaks logaritmilist skaalat joonlaual
Näited
Tuntud näited selliste skaalade kohta on järgmised:
- Richteri magnituudiskaala ja momendi magnituudiskaala (MMS) maavärinate tugevuse ja maa liikumise kohta.
- bel ja decibel ning neper akustilise võimsuse (valjuse) ja elektrilise võimsuse jaoks;
- f-stoppide lugemine fotograafilise ekspositsiooni suhtarvude jaoks;
- madalate tõenäosuste hindamine "üheksade" arvu järgi nende mitteesinemise tõenäosuse kümnendmurde laienduses: näiteks süsteem, mis ebaõnnestub tõenäosusega 10−5on 99,999% usaldusväärne: "viis üheksa".
- Entroopia termodünaamikas.
- Teave infoteoorias.
- Pinnase osakeste suuruse jaotuse kõverad
Mõned logaritmilised skaalad on konstrueeritud nii, et aluseks oleva suuruse suured väärtused (või suhtarvud) vastavad logaritmimõõdu väikestele väärtustele. Sellised skaalad on näiteks järgmised:
Logaritmiline skaala on ka graafiline skaala graafiku ühel või mõlemal küljel, kus number x on trükitud kaugusele c-log(x) punktist, mis on tähistatud numbriga 1. Loogaritmilised skaalad on olemas joonlaual ja nomogrammides kasutatakse sageli logaritmilisi skaalasid. Logaritmilisel skaalal kujutatakse võrdset suurusjärgu erinevust võrdse vahega. Kahe arvu geomeetriline keskmine on keskel asuv arv.
Logaritmiline graafikapaber oli enne arvutigraafika tulekut põhiline teaduslik vahend. Ühe logaritmilise skaalaga paberil võivad eksponentsiaalseid seadusi ja log-logaritmilise paberil võimsusseadusi kujutada sirgjoontena (vt semilogaritmiline graafik, log-logaritmiline graafik).
Küsimused ja vastused
K: Mis on logaritmiline skaala?
V: Logaritmiline skaala on skaala, mida kasutatakse siis, kui suur hulk suurusi on suur.
K: Millised on näited asjadest, mida saab mõõta logaritmilisel skaalal?
V: Maavärina tugevust, heli helitugevust, valguse intensiivsust, epideemiate leviku kiirust ja lahuste pH-d saab mõõta logaritmilisel skaalal.
K: Mille poolest erineb logaritmiline skaala tavapärasest lineaarsest skaalast?
V: Logaritmiline skaala põhineb pigem suurusjärkudel kui standardne lineaarne skaala. Skaala iga märgi väärtus on eelmise märgi väärtus korrutatud konstantsiga.
K: Mis on logaritmilise skaala kasutamise eelis?
V: Logaritmiline skaala võib vähendada suurt väärtuste vahemikku käepärasemaks, mis võib olla kasulik, kui tegemist on laia väärtuste vahemikku hõlmavate andmetega.
K: Mis on Stevensi võimsusseadus ja kuidas see on seotud logaritmiliste skaaladega?
V: Stevensi võimsusseadus kirjeldab, kuidas mõned meie meeled toimivad logaritmiliselt, kus tegeliku sisendtugevuse korrutamine lisab tajutud signaalitugevusele konstandi. See muudab logaritmilised skaalad nende sisendkoguste jaoks eriti sobivaks.
K: Miks on logaritmiline skaala eriti kasulik heli helitugevuse mõõtmiseks?
V: Meie kuulmismeel tajub sageduste võrdseid korrutisi kui võrdseid helikõrguse erinevusi, nii et logaritmiline skaala suudab seda suhet helisageduse ja tajutava helitugevuse vahel täpselt esitada.
K: Milline suhe on aluseks oleva suuruse väikeste kordajate ja logaritmilise mõõtme vahel enamikul logaritmilistel skaaladel?
V: Enamikul logaritmilistel skaaladel vastavad aluseks oleva suuruse väikesed kordajad (või suhtarvud) logaritmilise mõõtme väikestele (võimalik, et negatiivsetele) väärtustele.
